Le réglage fin de LLaMA réduit de moitié les besoins en mémoire, Tsinghua propose un optimiseur 4 bits

La formation et le réglage fin des grands modèles nécessitent des exigences élevées en matière de mémoire vidéo, et l'état de l'optimiseur est l'une des principales dépenses de la mémoire vidéo. Récemment, l'équipe de Zhu Jun et Chen Jianfei de l'Université Tsinghua a proposé un optimiseur 4 bits pour la formation des réseaux neuronaux, qui permet d'économiser la mémoire nécessaire à la formation du modèle et peut atteindre une précision comparable à celle d'un optimiseur de pleine précision.

Expérimenté sur de nombreuses tâches de pré-entraînement et de réglage fin, l'optimiseur 4 bits peut réduire la surcharge de mémoire liée au réglage fin du LLaMA-7B jusqu'à 57 % tout en conservant la précision.

Papier : https://arxiv.org/abs/2309.01507

Code : https://github.com/thu-ml/low-bit-optimizers

Gout d'étranglement en mémoire lors de la formation du modèle

De GPT-3, Gopher à LLaMA, il est devenu un consensus dans l'industrie selon lequel les grands modèles ont de meilleures performances. Cependant, en revanche, la taille de la mémoire vidéo d'un seul GPU a augmenté lentement, ce qui fait de la mémoire vidéo le principal goulot d'étranglement pour la formation de grands modèles. Comment former de grands modèles avec une mémoire GPU limitée est devenu un problème important.

Pour ce faire, nous devons d'abord clarifier les sources de consommation de mémoire vidéo. En fait, il existe trois types de sources, à savoir :

1. "Mémoire de données", incluant les données d'entrée et la valeur d'activation émise par chaque couche du réseau neuronal, sa taille est directement affectée par la taille du lot et résolution de l'image/longueur du contexte ;

2. "Mémoire du modèle", comprenant les paramètres du modèle, les dégradés et les états de l'optimiseur, sa taille est proportionnelle au nombre de paramètres du modèle

3. GPU Mémoire temporaire et autres caches utilisés dans les calculs du noyau. À mesure que la taille du modèle augmente, la proportion de mémoire vidéo du modèle augmente progressivement, devenant ainsi un goulot d'étranglement majeur.

La taille de l'état de l'optimiseur est déterminée par l'optimiseur utilisé. Actuellement, les optimiseurs AdamW sont souvent utilisés pour former des Transformers, qui doivent stocker et mettre à jour deux états de l'optimiseur pendant le processus de formation, à savoir le premier et le deuxième instant. Si le nombre de paramètres du modèle est N, alors le nombre d'états de l'optimiseur dans AdamW est 2N, ce qui représente évidemment une énorme surcharge de mémoire graphique.

Prenons LLaMA-7B comme exemple. Le nombre de paramètres de ce modèle est d'environ 7B si l'optimiseur AdamW pleine précision (32 bits) est utilisé pour l'affiner, la taille de la mémoire occupée par l'optimiseur. l'état est d'environ 52,2 Go. De plus, bien que l'optimiseur naïf SGD ne nécessite pas d'états supplémentaires et économise la mémoire occupée par l'état de l'optimiseur, les performances du modèle sont difficiles à garantir. Par conséquent, cet article se concentre sur la façon de réduire l’état de l’optimiseur dans la mémoire du modèle tout en garantissant que les performances de l’optimiseur ne sont pas compromises.

Méthodes pour économiser la mémoire de l'optimiseur

Actuellement, en termes d'algorithmes de formation, il existe trois méthodes principales pour économiser la mémoire de l'optimiseur :

1. Analyser l'état de l'optimiseur grâce à l'idée de faible niveau. décomposition de rang (Factorisation) Effectuer une approximation de bas rang ;

2. Évitez de sauvegarder la plupart des états de l'optimiseur en entraînant uniquement un petit ensemble de paramètres, tels que LoRA ;

3. format numérique de précision pour représenter l'état de l'optimiseur.

En particulier, Dettmers et al. (ICLR 2022) ont proposé un optimiseur 8 bits correspondant pour SGD avec momentum et AdamW, en utilisant la technologie de quantification par blocs et de format numérique exponentiel dynamique (format numérique exponentiel dynamique), il a atteint des résultats qui correspondent à l'optimiseur de précision d'origine dans des tâches telles que la modélisation du langage, la classification d'images, l'apprentissage auto-supervisé et la traduction automatique.

Sur cette base, cet article réduit encore la précision numérique de l'état de l'optimiseur à 4 bits, propose des méthodes de quantification pour différents états de l'optimiseur et propose enfin un optimiseur AdamW 4 bits. Parallèlement, cet article explore la possibilité de combiner des méthodes de compression et de décomposition de bas rang, et propose un optimiseur de facteur 4 bits. Cet optimiseur hybride bénéficie à la fois de bonnes performances et d'une meilleure efficacité mémoire. Cet article évalue les optimiseurs 4 bits sur un certain nombre de tâches classiques, notamment la compréhension du langage naturel, la classification d'images, la traduction automatique et le réglage fin des instructions de grands modèles.

Sur toutes les tâches, l'optimiseur 4 bits obtient des résultats comparables à l'optimiseur pleine précision tout en occupant moins de mémoire.

Configuration des problèmes

Un cadre pour un optimiseur efficace de mémoire basé sur la compression

Tout d'abord, nous devons comprendre comment introduire les opérations de compression dans les optimiseurs couramment utilisés, ce qui est donné par l'algorithme 1. où A est un optimiseur basé sur le gradient (tel que SGD ou AdamW). L'optimiseur prend en compte les paramètres existants w, le gradient g et l'état de l'optimiseur s et génère de nouveaux paramètres et un état de l'optimiseur. Dans l'algorithme 1, le s_t de pleine précision est transitoire, tandis que le s_t de basse précision (s_t) ̅ est conservé dans la mémoire du GPU. La raison importante pour laquelle cette méthode peut économiser de la mémoire vidéo est que les paramètres des réseaux de neurones sont souvent assemblés à partir des vecteurs de paramètres de chaque couche. Par conséquent, la mise à jour de l'optimiseur est également effectuée couche par couche/tenseur. Sous l'algorithme 1, l'état de l'optimiseur d'au plus un paramètre est laissé dans la mémoire sous forme de précision totale, et les états de l'optimiseur correspondant aux autres couches sont compressés. État. .

Méthode de compression principale : quantification

La quantification est une technologie qui utilise des valeurs numériques de faible précision pour représenter des données de haute précision. Cet article divise l'opération de quantification en deux parties : la normalisation (. normalisation) et la cartographie (cartographie), permettant ainsi une conception et une expérimentation plus légères de nouvelles méthodes de quantification. Les deux opérations de normalisation et de mappage sont appliquées séquentiellement sur les données pleine précision de manière élément par élément. La normalisation est chargée de projeter chaque élément du tenseur sur l'intervalle unitaire, où la normalisation du tenseur (normalisation par tenseur) et la normalisation par bloc (normalisation par bloc) sont définies comme suit :

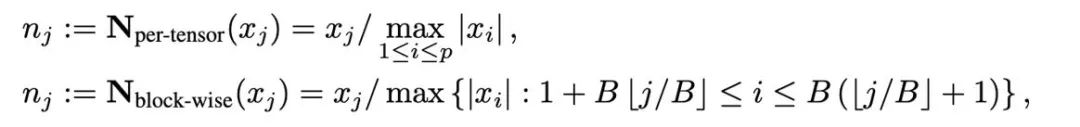
Différentes méthodes de normalisation ont des granularités différentes, leur capacité à gérer les valeurs aberrantes sera différente et ils entraîneront également une surcharge de mémoire supplémentaire différente. L'opération de mappage est chargée de mapper les valeurs normalisées sur des nombres entiers qui peuvent être représentés avec une faible précision. Formellement parlant, étant donné une largeur de bits b (c'est-à-dire que chaque valeur est représentée par b bits après quantification) et une fonction prédéfinie T

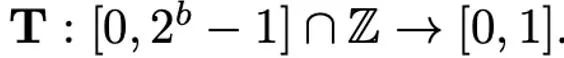
l'opération de mappage est définie comme :

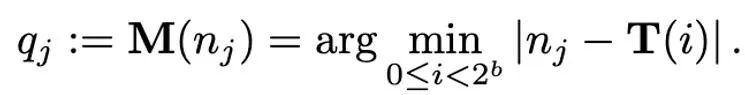
Par conséquent, Comment un T correctement conçu joue un rôle important dans la réduction des erreurs de quantification. Cet article considère principalement le mappage linéaire (linéaire) et le mappage exponentiel dynamique (exposant dynamique). Enfin, le processus de déquantification consiste à appliquer les opérateurs inverses de cartographie et de normalisation en séquence.

Méthode de compression du moment du premier ordre

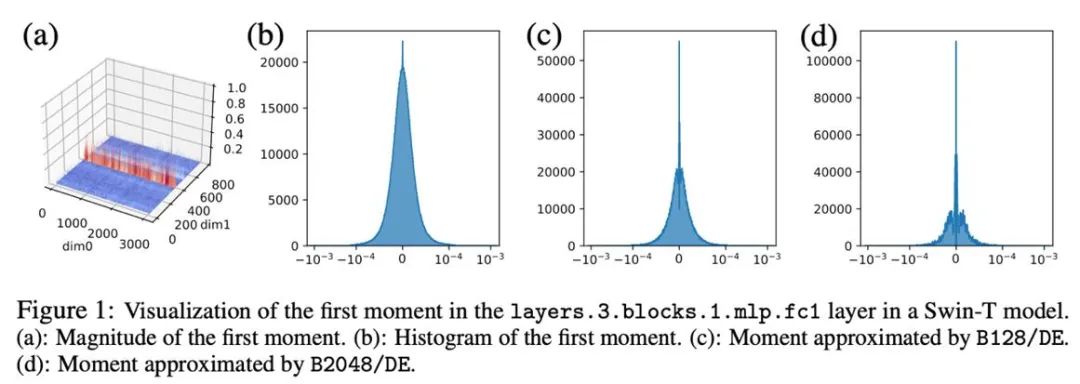
Ce qui suit propose principalement différentes méthodes de quantification pour l'état optimiseur (moment du premier ordre et moment du second ordre) d'AdamW. Pour les premiers instants, la méthode de quantification dans cet article est principalement basée sur la méthode de Dettmers et al (ICLR 2022), utilisant la normalisation de bloc (taille de bloc 2048) et la cartographie exponentielle dynamique.

Dans des expériences préliminaires, nous avons directement réduit la largeur de bit de 8 bits à 4 bits et avons constaté que le moment de premier ordre est très robuste à la quantification et a obtenu des résultats correspondants sur de nombreuses tâches, mais il se produit également sur certaines tâches. Perte de performances. Pour améliorer encore les performances, nous avons soigneusement étudié le modèle des premiers instants et avons constaté qu'il existe de nombreuses valeurs aberrantes dans un seul tenseur.

Des travaux antérieurs ont effectué des recherches sur le modèle de valeurs aberrantes dans les paramètres et les valeurs d'activation. La distribution des paramètres est relativement fluide, tandis que les valeurs d'activation sont distribuées selon les canaux. Cet article a révélé que la distribution des valeurs aberrantes dans l'état d'optimisation est complexe, certains tenseurs ayant des valeurs aberrantes réparties dans des lignes fixes et d'autres tenseurs ayant des valeurs aberrantes réparties dans des colonnes fixes.

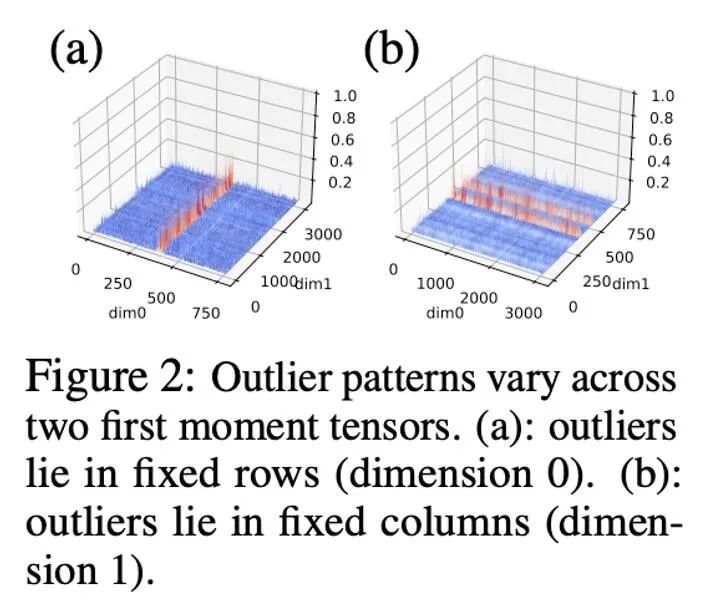
Pour les tenseurs avec distribution des valeurs aberrantes par colonnes, la normalisation des blocs par première ligne peut rencontrer des difficultés. Par conséquent, cet article propose d'utiliser des blocs plus petits avec une taille de bloc de 128, ce qui peut réduire l'erreur de quantification tout en maintenant la surcharge de mémoire supplémentaire dans une plage contrôlable. La figure ci-dessous montre l'erreur de quantification pour différentes tailles de bloc.

Méthode de compression des moments de second ordre

Par rapport aux moments de premier ordre, la quantification des moments de second ordre est plus difficile et apportera une instabilité à l'entraînement. Cet article détermine que le problème du point zéro est le principal goulot d'étranglement dans la quantification des moments du second ordre. De plus, une méthode de normalisation améliorée est proposée pour les distributions aberrantes mal conditionnées : la normalisation de rang 1. Cet article tente également la méthode de décomposition (factorisation) du moment du second ordre.

Problème du point zéro

Dans la quantification des paramètres, des valeurs d'activation et des gradients, les points zéro sont souvent indispensables, et ce sont aussi les points avec la fréquence la plus élevée après quantification. Cependant, dans la formule itérative d'Adam, la taille de la mise à jour est proportionnelle à la puissance -1/2 du deuxième moment, donc les changements dans la plage autour de zéro affecteront grandement la taille de la mise à jour, provoquant une instabilité.

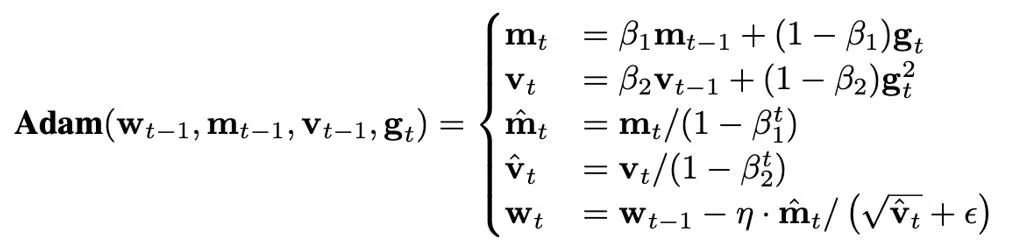
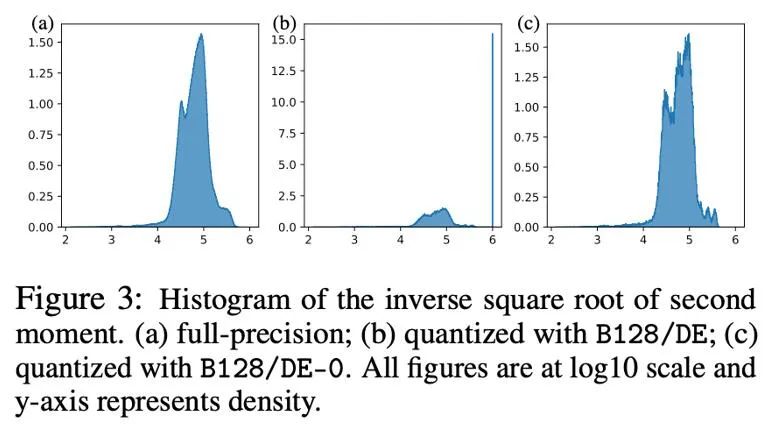
La figure suivante montre la distribution du deuxième moment d'Adam -1/2 puissance avant et après quantification sous la forme d'un histogramme, c'est-à-dire h (v)=1/(√v+10^( -6) ) . Si les zéros sont inclus (figure b), alors la plupart des valeurs sont poussées jusqu'à 10^6, ce qui entraîne d'importantes erreurs d'approximation. Une approche simple consiste à supprimer les zéros dans la carte exponentielle dynamique, après cela (figure c) l'approximation du deuxième moment devient plus précise. Dans des situations réelles, afin d'utiliser efficacement la capacité d'expression des valeurs numériques de faible précision, nous avons proposé d'utiliser une cartographie linéaire qui supprime les points zéro et avons obtenu de bons résultats expérimentaux.

Normalisation de rang 1

Basé sur la distribution complexe des valeurs aberrantes des moments du premier et du deuxième ordre, et inspiré de l'optimiseur SM3, cet article propose une nouvelle méthode de normalisation est appelée normalisation de rang 1. Pour un tenseur matriciel non négatif x∈R^(n×m), sa statistique unidimensionnelle est définie comme :

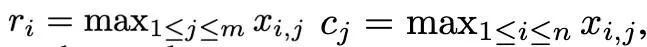
Ensuite, la normalisation de rang 1 peut être définie comme :

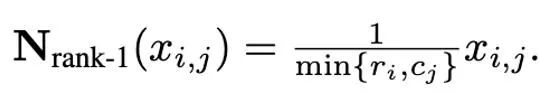
La normalisation de rang 1 exploite les informations unidimensionnelles du tenseur de manière plus fine et peut gérer les valeurs aberrantes par ligne ou par colonne de manière plus intelligente et efficace. De plus, la normalisation de rang 1 peut être facilement généralisée aux tenseurs de grande dimension, et à mesure que la taille du tenseur augmente, la surcharge de mémoire supplémentaire qu'elle génère est inférieure à celle de la normalisation de bloc.

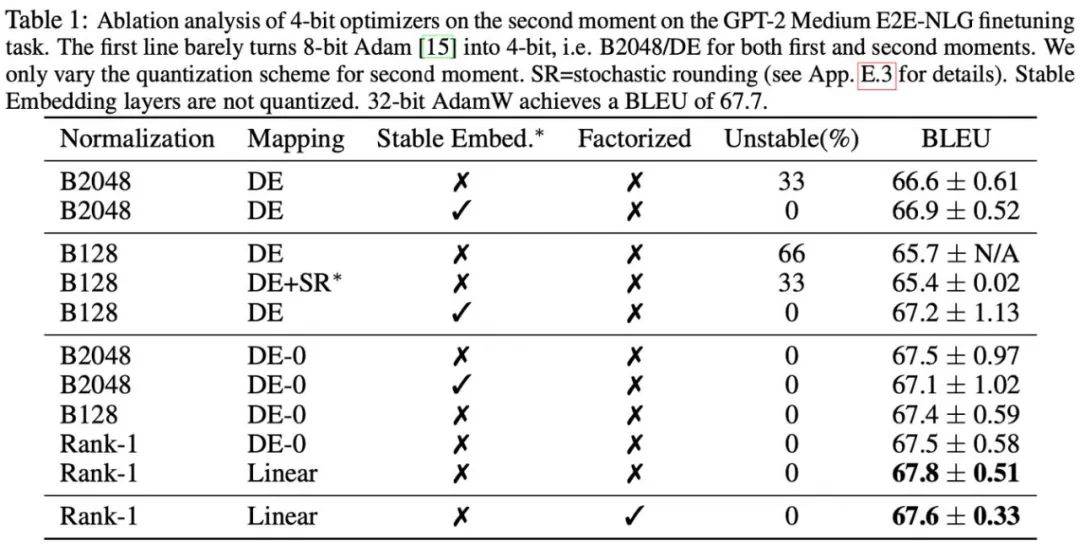
De plus, cet article a révélé que la méthode de décomposition de bas rang pour les moments de second ordre dans l'optimiseur Adafactor peut efficacement éviter le problème du point zéro, c'est pourquoi la combinaison de méthodes de décomposition et de quantification de bas rang a également été explorée. La figure ci-dessous montre une série d'expériences d'ablation pour les moments du second ordre, ce qui confirme que le problème du point zéro est le goulot d'étranglement de la quantification des moments du second ordre. Elle vérifie également l'efficacité des méthodes de normalisation de rang 1 et de décomposition de rang bas.

Résultats expérimentaux

Sur la base des phénomènes observés et des méthodes d'utilisation, la recherche a finalement proposé deux optimiseurs de faible précision : 4-bit AdamW et 4-bit Factor, et les a comparés à d'autres optimiseurs, y compris AdamW 8 bits, Adafactor, SM3. Les études ont été sélectionnées pour être évaluées sur un large éventail de tâches, notamment la compréhension du langage naturel, la classification d'images, la traduction automatique et le réglage fin des instructions de grands modèles. Le tableau ci-dessous montre les performances de chaque optimiseur sur différentes tâches.

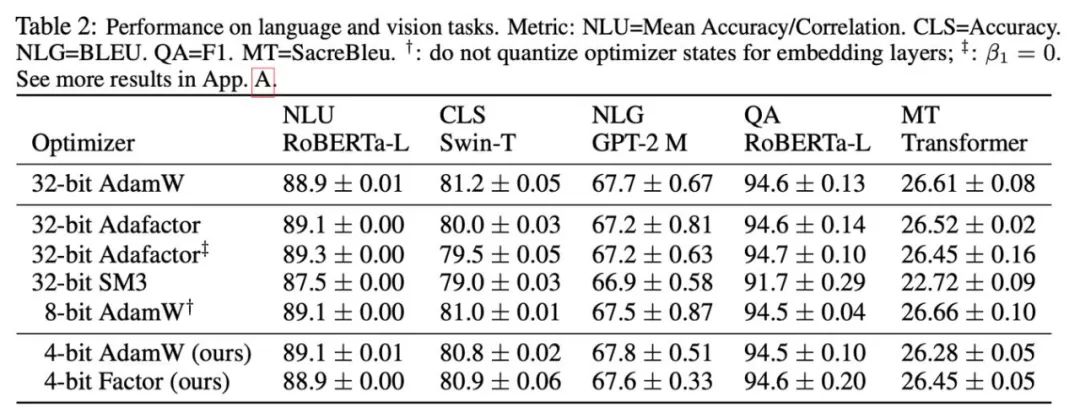
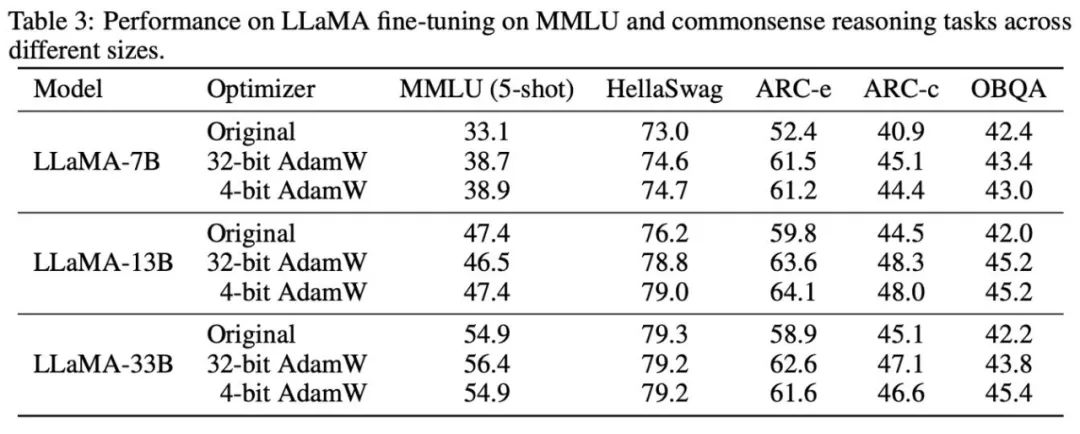
On peut voir que sur toutes les tâches de réglage fin, y compris NLU, QA, NLG, l'optimiseur 4 bits peut égaler ou même dépasser l'AdamW 32 bits, tandis que sur tous les pré- tâches de formation, l'optimiseur CLS, MT, 4 bits atteint un niveau comparable à une précision totale. Il ressort de la tâche de réglage fin des instructions qu'AdamW 4 bits ne détruit pas la capacité des modèles pré-entraînés et peut en même temps mieux leur permettre d'acquérir la capacité de se conformer aux instructions.

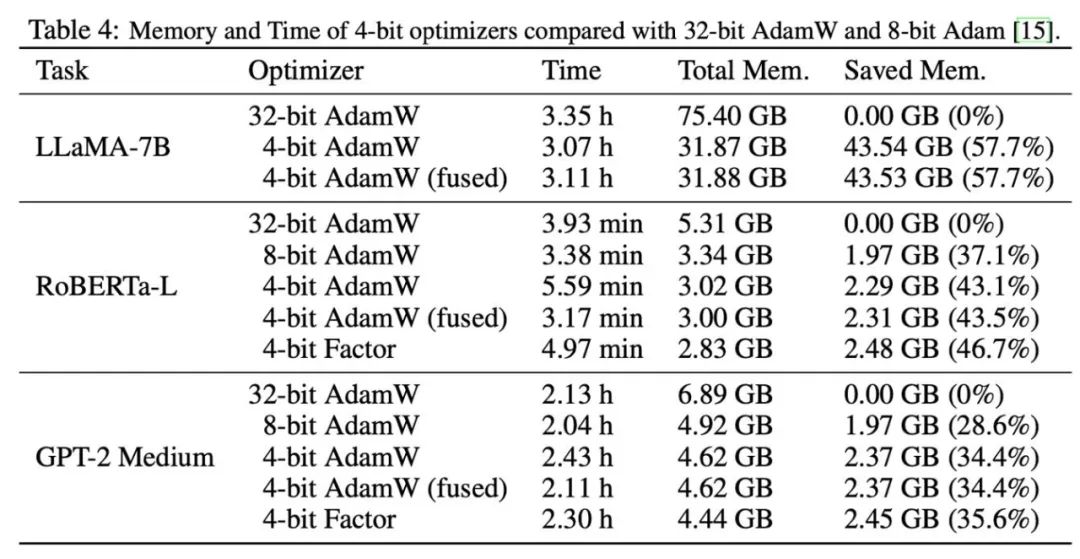
Après cela, nous avons testé la mémoire et l'efficacité de calcul de l'optimiseur 4 bits, et les résultats sont présentés dans le tableau ci-dessous. Par rapport à l'optimiseur 8 bits, l'optimiseur 4 bits proposé dans cet article peut économiser plus de mémoire, avec une économie maximale de 57,7 % dans l'expérience de réglage fin LLaMA-7B. De plus, nous fournissons une version d'opérateur de fusion d'AdamW 4 bits, qui peut économiser de la mémoire sans affecter l'efficacité des calculs. Pour la tâche de réglage fin des instructions de LLaMA-7B, AdamW 4 bits apporte également des effets d'accélération à la formation en raison de la pression réduite du cache. Les paramètres expérimentaux détaillés et les résultats peuvent être trouvés dans le lien papier.

Remplacez une ligne de code pour l'utiliser dans PyTorch

import lpmmoptimizer = lpmm.optim.AdamW (model.parameters (), lr=1e-3, betas=(0.9, 0.999))

Nous fournissons un optimiseur 4 bits prêt à l'emploi, il vous suffit de remplacer l'optimiseur d'origine par un optimiseur 4 bits, actuellement prend en charge les versions basse précision d'Adam et SGD. Dans le même temps, nous fournissons également une interface permettant de modifier les paramètres de quantification afin de prendre en charge des scénarios d'utilisation personnalisés.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!