Réflexion profonde | Où se situe la limite des capacités des grands modèles ?

Si nous disposons de ressources illimitées, telles que des données infinies, une puissance de calcul infinie, des modèles infinis, des algorithmes d'optimisation parfaits et des performances de généralisation, le modèle pré-entraîné résultant peut-il être utilisé pour résoudre tous les problèmes ?

C'est une question qui préoccupe tout le monde, mais les théories existantes sur l'apprentissage automatique ne peuvent pas y répondre. Cela n'a rien à voir avec la théorie de la capacité d'expression, car le modèle est infini et la capacité d'expression est naturellement infinie. Cela n’a pas non plus d’importance pour la théorie de l’optimisation et de la généralisation, car nous supposons que les performances d’optimisation et de généralisation de l’algorithme sont parfaites. En d’autres termes, les problèmes des recherches théoriques antérieures n’existent plus ici !

Aujourd'hui, je vais vous présenter l'article Sur le pouvoir des modèles de fondation que j'ai publié à l'ICML'2023, et donner une réponse du point de vue de la théorie des catégories.

Qu'est-ce que la théorie des catégories ?

Si vous n'êtes pas étudiant en mathématiques, vous n'êtes peut-être pas familier avec la théorie des catégories. La théorie des catégories est appelée les mathématiques des mathématiques et fournit un langage de base pour les mathématiques modernes. Presque tous les domaines mathématiques modernes sont décrits dans le langage de la théorie des catégories, comme la topologie algébrique, la géométrie algébrique, la théorie des graphes algébriques, etc. La théorie des catégories est l'étude de la structure et des relations. Elle peut être considérée comme une extension naturelle de la théorie des ensembles : dans la théorie des ensembles, un ensemble contient plusieurs éléments différents ; dans la théorie des catégories, nous enregistrons non seulement les éléments, mais également la relation entre les éléments ; .

Martin Kuppe a un jour dessiné une carte des mathématiques, plaçant la théorie des catégories en haut de la carte, brillant dans tous les domaines des mathématiques :

Il existe de nombreuses introductions à la théorie des catégories sur Internet. Parlons brièvement de quelques-unes. concepts de base ici :

Perspective théorique des catégories de l'apprentissage supervisé

Au cours des dix dernières années, les gens ont mené de nombreuses recherches autour du cadre d'apprentissage supervisé et ont obtenu de nombreuses belles conclusions. Cependant, ce cadre limite également la compréhension des algorithmes d’IA, ce qui rend extrêmement difficile la compréhension de grands modèles pré-entraînés. Par exemple, les théories de généralisation existantes sont difficiles à expliquer les capacités d’apprentissage intermodal des modèles.

Pouvons-nous apprendre ce foncteur en échantillonnant ses données d'entrée et de sortie ?

Remarquez que dans ce processus nous n'avons pas pris en compte la structure interne des deux catégories X et Y. En fait, l’apprentissage supervisé ne fait aucune hypothèse sur la structure au sein des catégories, on peut donc considérer qu’il n’y a aucune relation entre deux objets au sein des deux catégories. On peut donc considérer X et Y comme deux ensembles. À l’heure actuelle, le fameux théorème de la théorie de la généralisation nous dit que sans hypothèses supplémentaires, il est impossible d’apprendre le foncteur de X à Y (à moins d’avoir des échantillons massifs).

À première vue, cette nouvelle perspective ne sert à rien. Qu'il s'agisse d'ajouter des contraintes aux catégories ou d'ajouter des contraintes aux foncteurs, il ne semble y avoir aucune différence essentielle. En fait, la nouvelle perspective s’apparente davantage à une version castrée du cadre traditionnel : elle ne mentionne même pas la notion de fonction de perte, extrêmement importante dans l’apprentissage supervisé, et ne peut pas être utilisée pour analyser les propriétés de convergence ou de généralisation de la formation. algorithme. Alors, comment comprendre cette nouvelle perspective ?

Je pense que la théorie des catégories offre une vue d’ensemble. Il ne remplace pas et ne doit pas remplacer le cadre d’apprentissage supervisé original plus spécifique, ni être utilisé pour produire de meilleurs algorithmes d’apprentissage supervisé. Au lieu de cela, les cadres d'apprentissage supervisé sont ses « sous-modules », des outils qui peuvent être utilisés pour résoudre des problèmes spécifiques. Par conséquent, la théorie des catégories ne se soucie pas des fonctions de perte ou des procédures d’optimisation – celles-ci s’apparentent davantage aux détails de mise en œuvre de l’algorithme. Il se concentre davantage sur la structure des catégories et des foncteurs, et tente de comprendre si un certain foncteur peut être appris. Ces problèmes sont extrêmement difficiles dans les cadres traditionnels d’apprentissage supervisé, mais deviennent plus simples dans la perspective des catégories.

Perspective de la théorie des catégories de l'apprentissage auto-supervisé

Tâches et catégories de pré-formation

Clarifions d'abord la définition des catégories sous la tâche de pré-formation. En fait, si nous ne concevons aucune tâche de pré-formation, il n'y aura aucune relation entre les objets de la catégorie mais après avoir conçu les tâches de pré-formation, nous injecterons des connaissances humaines préalables dans la catégorie sous forme de tâches ; Et ces structures deviennent les connaissances que possède le grand modèle.

Plus précisément :

En d'autres termes, après avoir défini la tâche de pré-formation sur un ensemble de données, nous définissons une catégorie qui contient la structure de relation correspondante. L'objectif d'apprentissage de la tâche de pré-formation est de permettre au modèle de bien apprendre cette catégorie. Plus précisément, nous examinons le concept de modèle idéal.

Modèle idéal

Ici, « indépendant des données » signifie que est prédéfini avant de voir les données mais l'indice f signifie que f et peuvent être utilisés via des appels de boîte noire Ces ; deux fonctions. En d’autres termes, est une fonction « simple », mais peut s’appuyer sur les capacités du modèle f pour représenter des relations plus complexes. Cela n'est peut-être pas facile à comprendre. Utilisons un algorithme de compression comme analogie. L'algorithme de compression lui-même peut dépendre des données, par exemple il peut être spécialement optimisé pour la distribution des données. Cependant, en tant que fonction indépendante des données , elle ne peut pas accéder à la distribution des données, mais elle peut appeler l'algorithme de compression pour décompresser les données, car l'opération « d'appeler l'algorithme de compression » est indépendante des données.

Pour différentes tâches de pré-formation, nous pouvons définir différentes :

Par conséquent, nous pouvons dire : Le processus d'apprentissage pré-formation est le processus de recherche du modèle idéal f.

Cependant, même si est certain, par définition, le modèle idéal n'est pas unique. Théoriquement, le modèle f pourrait être super intelligent et capable de tout faire sans apprendre les données en C. Dans ce cas, nous ne pouvons pas faire de déclaration significative sur les capacités de f . Par conséquent, nous devrions regarder l'autre côté du problème :

Étant donné une catégorie C définie par une tâche pré-entraînée, pour tout idéal f , quelles tâches peut-elle résoudre ?

C'est la question centrale à laquelle nous souhaitons répondre au début de cet article. Introduisons d’abord un concept important.

Intégration de Yoneda

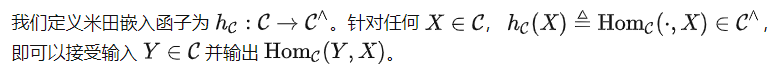
Il est facile de montrer que est le modèle idéal le moins capable car étant donné d'autres modèles idéaux f , toutes les relations dans sont également contenues dans f . Dans le même temps, c'est aussi l'objectif ultime de l'apprentissage du modèle pré-formation sans autres hypothèses supplémentaires. Par conséquent, pour répondre à notre question principale, nous considérons spécifiquement ci-dessous.

Réglage rapide : ce n'est qu'en voyant plus que vous pourrez en savoir plus

Pouvez-vous résoudre une certaine tâche T ? Pour répondre à cette question, nous introduisons d’abord l’un des théorèmes les plus importants de la théorie des catégories.

Yoneda Lemma

C'est-à-dire que peut calculer T(X) en utilisant ces deux représentations. Cependant, notez que l'invite de tâche P doit être envoyée via au lieu de , ce qui signifie que nous obtiendrons (P) au lieu de T comme entrée pour . Cela conduit à une autre définition importante dans la théorie des catégories.

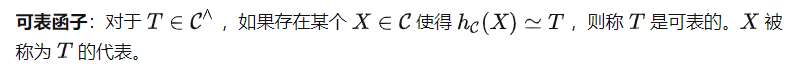
Sur la base de cette définition, nous pouvons obtenir le théorème suivant (preuve omise).

Théorème 1 et corollaire

Il convient de mentionner que certains indices pour l'algorithme de réglage ne sont pas nécessairement des objets de la catégorie C, mais peuvent être des représentations dans l'espace des fonctionnalités. Cette approche a le potentiel de prendre en charge des tâches plus complexes que les tâches représentables, mais l'amélioration dépend de la puissance expressive de l'espace des fonctionnalités. Nous fournissons ci-dessous un corollaire simple du théorème 1.

Corollaire 1 Pour la tâche de pré-entraînement consistant à prédire l'angle de rotation de l'image [4], il est suggéré que le réglage ne peut pas résoudre des tâches complexes en aval telles que la segmentation ou la classification.

Preuve : la tâche de pré-entraînement consistant à prédire les angles de rotation de l'image fait pivoter une image donnée de quatre angles différents : 0°, 90°, 180° et 270°, et permet au modèle de faire des prédictions. Ainsi, les catégories définies par cette tâche de pré-formation placent chaque objet dans un groupe de 4 éléments. Évidemment, des tâches comme la segmentation ou la classification ne peuvent pas être représentées par des objets aussi simples.

Le corollaire 1 est un peu contre-intuitif, car l'article original mentionnait [4] que le modèle obtenu à l'aide de cette méthode peut résoudre partiellement des tâches en aval telles que la classification ou la segmentation. Cependant, dans notre définition, résoudre la tâche signifie que le modèle doit générer le résultat correct pour chaque entrée, donc être partiellement correct n'est pas considéré comme un succès. Cela est également cohérent avec la question mentionnée au début de notre article : avec le soutien de ressources illimitées, la tâche pré-entraînée consistant à prédire les angles de rotation de l'image peut-elle être utilisée pour résoudre des tâches complexes en aval ? Le corollaire 1 donne une réponse négative.

Réglage fin : représentation sans perte d'informations

Conseils selon lesquels la capacité de réglage est limitée, alors qu'en est-il de l'algorithme de réglage fin ? Basé sur le théorème de développement des foncteurs de Yoneda (voir Proposition 2.7.1 dans [5]), nous pouvons obtenir le théorème suivant.

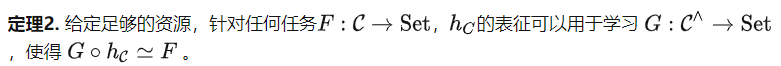
Le théorème 2 considère les tâches en aval basées sur la structure du C plutôt que sur le contenu des données dans l'ensemble de données. Par conséquent, la catégorie définie par la tâche de pré-entraînement mentionnée précédemment consistant à prédire l'angle d'une image pivotée a toujours une structure de groupe très simple. Mais d’après le théorème 2, nous pouvons l’utiliser pour résoudre des tâches plus diverses. Par exemple, nous pouvons mapper tous les objets sur la même sortie, ce qui n'est pas possible avec le réglage des indices. Le théorème 2 clarifie l'importance des tâches de pré-formation, puisque de meilleures tâches de pré-formation créeront des catégories C plus puissantes, améliorant ainsi encore le potentiel de réglage fin du modèle.

Il existe deux malentendus courants à propos du théorème 2. Tout d’abord, même si la catégorie C contient une grande quantité d’informations, le théorème 2 ne fournit qu’une limite supérieure approximative, disant que enregistre toutes les informations en C et a le potentiel de résoudre n’importe quelle tâche, mais il ne dit pas que n’importe quelle un algorithme de réglage fin peut atteindre cet objectif. Deuxièmement, le théorème 2 ressemble à première vue à une théorie surparamétrée. Cependant, ils analysent différentes étapes de l’apprentissage auto-supervisé. L'analyse paramétrique est l'étape de pré-formation, ce qui signifie que sous certaines hypothèses, tant que le modèle est suffisamment grand et que le taux d'apprentissage est suffisamment faible, les erreurs d'optimisation et de généralisation seront très faibles pour la tâche de pré-formation. Le théorème 2 analyse l'étape de mise au point après la pré-formation, affirmant que cette étape a un grand potentiel.

Discussion et résumé

Apprentissage supervisé et apprentissage auto-supervisé. Du point de vue de l'apprentissage automatique, l'apprentissage auto-supervisé reste un type d'apprentissage supervisé, mais la manière d'obtenir des étiquettes est plus intelligente. Mais du point de vue de la théorie des catégories, l’apprentissage auto-supervisé définit la structure au sein d’une catégorie, tandis que l’apprentissage supervisé définit la relation entre les catégories. Par conséquent, ils se trouvent dans des parties différentes de la carte de l’intelligence artificielle et font des choses complètement différentes.

Scénarios applicables. Puisque l’hypothèse de ressources infinies a été envisagée au début de cet article, de nombreux amis peuvent penser que ces théories ne peuvent être véritablement établies que dans le vide. Ce n'est pas le cas. Dans notre processus de dérivation actuel, nous avons uniquement considéré le modèle idéal et la fonction prédéfinie . En fait, tant que est déterminé, tout modèle f pré-entraîné (même dans la phase d'initialisation aléatoire) peut calculer f(X) pour l'entrée XC, et ainsi utiliser pour calculer la relation entre deux objets. Autrement dit, tant que est déterminé, chaque modèle pré-entraîné correspond à une catégorie, et le but du pré-entraînement est juste d'aligner en continu cette catégorie avec la catégorie définie par la tâche de pré-entraînement . Par conséquent, notre théorie est valable pour chaque modèle pré-entraîné.

Formule de base. Beaucoup de gens disent que si l’IA dispose réellement d’un ensemble de supports théoriques, alors elle devrait reposer sur une ou plusieurs formules simples et élégantes. Je pense que si nous devons utiliser une formule de théorie des catégories pour décrire les capacités des grands modèles, cela devrait être ce que nous avons mentionné précédemment :

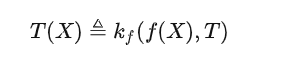
Pour les amis qui sont familiers avec les grands modèles, après une compréhension approfondie de la signification de cette formule, peut-être Vous pensez peut-être que cette formule est absurde, mais elle exprime simplement le mode de fonctionnement du grand modèle actuel en utilisant une formule mathématique relativement complexe.

Mais ce n’est pas le cas. La science moderne est basée sur les mathématiques, et les mathématiques modernes sont basées sur la théorie des catégories, et le théorème le plus important de la théorie des catégories est le lemme de Yoneda. La formule que j'ai écrite démonte l'isomorphisme du lemme de Yoneda en une version asymétrique, mais c'est exactement la même chose que la manière d'ouvrir le grand modèle.

Je ne pense pas que ce soit une coïncidence. Si la théorie des catégories peut éclairer diverses branches des mathématiques modernes, elle peut également éclairer la voie à suivre pour l’intelligence artificielle générale.

Cet article s'inspire de la coopération étroite et à long terme avec l'équipe Qianfang de l'Institut de recherche sur l'intelligence artificielle Zhiyuan de Pékin.

Lien original : https://mp.weixin.qq.com/s/bKf3JADjAveeJDjFzcDbkw

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!