Maison >développement back-end >C++ >Imprimer la sous-matrice carrée de somme maximale d'une taille donnée dans le programme C
Imprimer la sous-matrice carrée de somme maximale d'une taille donnée dans le programme C
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-09-07 13:53:041408parcourir
Étant donné une matrice NxN, trouvez une sous-matrice MxM où M=1 telle que la somme de tous les éléments de la matrice MxM soit maximale. L'entrée de la matrice NxN peut contenir des valeurs nulles, entières positives et entières négatives.
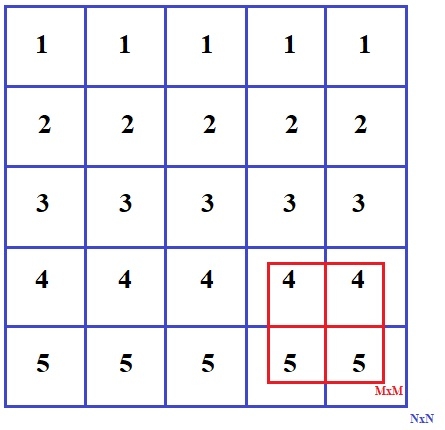
Exemple
Input:
{{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5} }
Output:
4 4
5 5Le problème ci-dessus peut être résolu avec une solution simple, nous pouvons prendre la matrice entière NxN puis trouver toutes les matrices MxM possibles et trouver leur somme puis imprimer celle avec la matrice MxM à somme maximale. Cette méthode est simple mais nécessite une complexité temporelle O(N^2.M^2), nous essayons donc de trouver une méthode avec moins de complexité temporelle.
Algorithme
Start
Step 1 -> Declare Function void matrix(int arr[][size], int k)
IF k>size
Return
Declare int array[size][size]
Loop For int j=0 and j<size and j++
Set sum=0
Loop for int i=0 and i<k and i++
Set sum=sum + arr[i][j]
End
Set array[0][j]=sum
Loop For int i=1 and i<size-k+1 and i++
Set sum=sum+(arr[i+k-1]][j]-arr[i-1][j]
Set arrayi][j]=sum
End
Set int maxsum = INT_MIN and *pos = NULL
Loop For int i=0 and i<size-k+1 and i++)
Set int sum = 0
Loop For int j = 0 and j<k and j++
Set sum += array[i][j]
End
If sum > maxsum
Set maxsum = sum
Set pos = &(arr[i][0])
End
Loop For int j=1 and j<size-k+1 and j++
Set sum += (array[i][j+k-1] - array[i][j-1])
IF sum > maxsum
Set maxsum = sum
Set pos = &(arr[i][j])
End
End
End
Loop For int i=0 and i<k and i++
Loop For int j=0 and j<k and j++
Print *(pos + i*size + j)
End
Print </p><p>
End
Step 2 -> In main()
Declare int array[size][size] = {{1, 1, 1, 1, 1}, {2, 2, 2, 2, 2}, {3, 3, 3, 3, 3}, {4, 4, 4, 4, 4}, {5, 5, 5, 5, 5}}
Declare int k = 2
Call matrix(array, k)
StopExemple
#include <bits/stdc++.h>
using namespace std;
#define size 5
void matrix(int arr[][size], int k){
if (k > size) return;
int array[size][size];
for (int j=0; j<size; j++){
int sum = 0;
for (int i=0; i<k; i++)
sum += arr[i][j];
array[0][j] = sum;
for (int i=1; i<size-k+1; i++){
sum += (arr[i+k-1][j] - arr[i-1][j]);
array[i][j] = sum;
}
}
int maxsum = INT_MIN, *pos = NULL;
for (int i=0; i<size-k+1; i++){
int sum = 0;
for (int j = 0; j<k; j++)
sum += array[i][j];
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][0]);
}
for (int j=1; j<size-k+1; j++){
sum += (array[i][j+k-1] - array[i][j-1]);
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][j]);
}
}
}
for (int i=0; i<k; i++){
for (int j=0; j<k; j++)
cout << *(pos + i*size + j) << " ";
cout << endl;
}
}
int main(){
int array[size][size] = {
{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5},
};
int k = 2;
matrix(array, k);
return 0;
}Sortie
Si nous exécutons le programme ci-dessus, il générera la sortie suivante
4 4 5 5
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

