Quelle est l'aire d'un cercle inscrit dans un losange ?

Le cercle inscrit d'un losange est tangent à ses quatre côtés et à ses quatre extrémités. Les côtés d'un losange sont tangents au cercle.

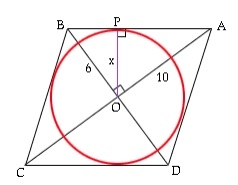
Ici, r est le rayon trouvé en utilisant a et la diagonale de la valeur donnée.

Maintenant, le triangle d'aire AOB = ½ * OA * OB = ½ * AB * r (tous deux utilisant la formule ½*b*h).

½ *a/2*b/2 = ½ *( √ (a2/4 + b²/4))*r

a*b/8 = √ (a²+ b ² )*r /4

r = a*b/ 2√ (a²+ b² )

Aire du cercle = π*r*r = π*(a²*b ²)/4(a² support>+ b² )

Exemple

Diagonales du losange 5 et 10.

La zone est de 15,700000

Exemple de code

Démonstration en temps réel

#include <stdio.h>
int main(void) {
   int a = 5; int b= 10;
   float pie = 3.14;
   float area = (float)((pie*a*a*b*b)/(4*((a*a)+(b*b))));
   printf("The area of circle inscribed in the rhombus of diagonal %d and %d is %f",a,b,area);
   return 0;
}

Sortie

The area of circle inscribed in the rhombus of diagonal 5 and 10 is 15.700000

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!