Quel est le plus grand carré inscrit dans un triangle équilatéral ?

Une forme plane ou solide qui est inscritedans une autre forme géométrique ou solide est enfermée et "étroitement ajustée" à l'intérieur de celle-ci. Dire "un carré est inscrit dans un triangle" signifie exactement la même chose que "un triangle est circonscrit dans un carré".

Le plus grand carré pouvant être inscrit dans un triangle équilatéral−

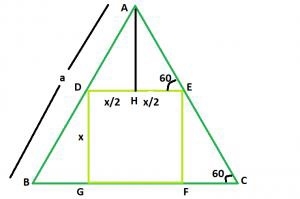
Le plus grand carré pouvant être inscrit dans un triangle équilatéral−

Donnons un exemple,

Input: 5
Output: 2.32

Explication

Un côté d'un carré est x .

Maintenant, AH est perpendiculaire à DE.

DE est parallèle à BC, angle AED = angle ACB = 60

Dans le triangle EFC,

⇒ Sin60 = x/ EC

⇒ √3 / 2 = x/EC

⇒ Ec = 2x / √3

in triangle ahe,

⇒ cos 60 = x / 2ae

⇒ 1/2 = x / 2ae

⇒ ae = x

côté du triangle ac = 2x/√3 + x. Maintenant,

a = 2x/√3 + x

x = a/(1 + 2/√3) = 0,464a

Exemple

Démonstration

#include <stdio.h>
#include <math.h>
int main() {
   float a = 5;
   float area = 0.464 * a;
   printf("The area is : %f",area);
   return 0;
}

Sortie

The area is : 2.320000

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!