Comment comprendre l'algorithme a priori des règles d'association

Comprendre l'algorithme apriori des règles d'association : L'algorithme Apriori est le premier algorithme d'exploration de règles d'association et l'algorithme le plus classique. Il utilise une méthode itérative de recherche couche par couche pour trouver la relation entre les ensembles d'éléments dans le. base de données pour former des règles. Le processus consiste en une connexion [opérations de type matricielle] et un élagage [suppression des résultats intermédiaires inutiles].

Comprendre l'algorithme a priori de la règle d'association :

1. Concepts

Tableau 1 Base de données des transactions d'un supermarché

pain, thé

Numéro de transaction TID

交易号TID	顾客购买的商品	交易号TID	顾客购买的商品
T1	bread, cream, milk, tea	T6	bread, tea
T2	bread, cream, milk	T7	beer, milk, tea
T3	cake, milk	T8	bread, tea
T4	milk, tea	T9	bread, cream, milk, tea
T5	bread, cake, milk	T10	bread, milk, tea

Article acheté par le client

Numéro de transaction TID

Article acheté par le client

T1

pain, crème, lait, thé

T6

T2

pain, crème, lait

T7

bière, lait, thé

T3

gâteau au lait

T8

pain, thé

T4

lait, thé

T9

pain, crème, lait, thé

T5 td>

pain, gâteau, lait

T10

pain, lait, thé

Définition 1 : Soit I={i1,i2,…,im}, être un ensemble de m éléments différents, chaque ik est appelé Pour un projet. L'ensemble I des items est appelé itemset . Le nombre de ses éléments est appelé la longueur de l'ensemble d'éléments, et un ensemble d'éléments de longueur k est appelé un k-itemset. Dans l'exemple, chaque produit est un élément, l'ensemble d'éléments est I={pain, bière, gâteau, crème, lait, thé} et la longueur de I est 6.

Définition 2 : Chaque transaction T est un enfant de l'ensemble d'éléments que j'ai défini . A chaque transaction correspond un numéro de transaction d'identification unique, enregistré comme TID. Toutes les transactions constituent la base de données des transactions D, |D| est égal au nombre de transactions dans D. L'exemple contient 10 transactions, donc |D|=10.

Définition 3 : Pour l'ensemble d'éléments X, définissez le nombre (X⊆T) comme le nombre de transactions contenant X dans la quantité de l'ensemble de transactions D , alors le support de l'ensemble d'éléments X est :

support(X)=count(X⊆T)/|D

Dans l'exemple, X={pain, lait} apparaît en T1, T2, T5, T9 et T10, le support est donc de 0,5.

Définition 4 : Le support minimum est le minimum de l'ensemble d'éléments Le seuil de support, noté SUPmin, représente l'importance minimale des règles d'association qui intéressent les utilisateurs. Les ensembles d'éléments avec supportent au moins SUPmin sont appelés ensembles fréquents , et les ensembles fréquents d'une longueur k sont appelés ensembles k-fréquents. Si SUPmin est réglé sur 0,3, le support de {pain, lait} dans l'exemple est de 0,5, il s'agit donc d'un ensemble à 2 fréquences.

Définition 5 : La règle d'association est une implication :

R : Indique que si l'ensemble d'éléments X apparaît dans une certaine transaction, Y apparaîtra également avec une certaine probabilité. Les règles d'association qui intéressent les utilisateurs peuvent être mesurées selon deux critères : le soutien et la crédibilité.

Définition 6

: Le support de la règle d'association R est un transaction Le rapport du nombre de transactions dans l'ensemble contenant à la fois X et Y à |D|. C'est-à-dire : support(X⇒Y)=count(X⋃Y)/|D|

Le support reflète la probabilité que

X et Y apparaissent en même temps temps. La prise en charge des règles d'association est égale à la prise en charge des ensembles fréquents.

Définition 7

: Pour la règle d'association R, crédibilité Elle fait référence au rapport du nombre de transactions contenant X et Y au nombre de transactions contenant X. C'est-à-dire : confidence(X⇒Y)=support(X⇒Y)/support(X)

La confiance reflète que si

X est inclus dans la transaction, puis La probabilité que la transaction contienne Y. D’une manière générale, seules les règles d’association bénéficiant d’un haut niveau de support et de crédibilité intéressent les utilisateurs.

Définition 8 : Définir le support minimum et la crédibilité minimale des règles d'association comme SUPmin et CONFmin. Si le support et la crédibilité de la règle R ne sont pas inférieurs à SUPmin et CONFmin, on parle de

règle d'association forte

. L’objectif de l’exploration de règles d’association est de trouver des règles d’association solides pour guider la prise de décision des commerçants. Ces huit définitions incluent plusieurs concepts de base importants liés aux règles d'association. Il existe deux problèmes principaux dans l'exploration de règles d'association :

1. Recherchez tous les ensembles d'éléments fréquents dans la base de données des transactions qui sont supérieurs ou égaux au support minimum spécifié par l'utilisateur.
2. Utilisez des ensembles d'éléments fréquents pour générer les règles d'association requises et filtrez les règles d'association fortes en fonction de la crédibilité minimale définie par l'utilisateur.

Actuellement, les chercheurs étudient principalement le premier problème. Il est difficile de trouver des ensembles fréquents, mais il est relativement facile de générer des règles d'association fortes avec des ensembles fréquents.

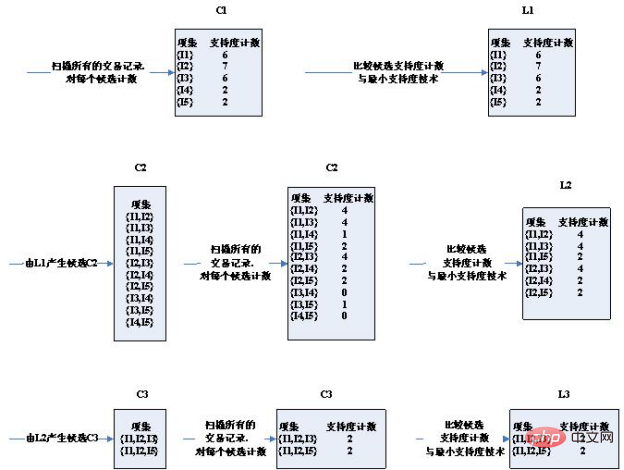
2. Base théorique

Tout d'abord, regardons les propriétés d'un ensemble fréquent.

Théorème : Si l'ensemble d'éléments X est un ensemble fréquent, alors ses sous-ensembles non vides sont tous des ensembles fréquents .

Selon le théorème, étant donné un ensemble d'éléments X d'un ensemble k-fréquent, tous les sous-ensembles d'ordre k-1 des ensembles d'éléments de deux ensembles fréquents k-1 ne diffèrent que par un élément et sont égaux à X après avoir été connectés. Cela prouve que l’ensemble k-candidat généré par la concaténation de k-1 ensembles fréquents couvre l’ensemble k-fréquent. Dans le même temps, si l'ensemble d'éléments Y dans l'ensemble k-candidat contient un sous-ensemble d'ordre k-1 qui n'appartient pas à l'ensemble fréquent k-1, alors Y ne peut pas être un ensemble fréquent et doit être élagué de l'ensemble candidat. L'algorithme Apriori tire parti de cette propriété des ensembles fréquents.

3. Étapes de l'algorithme :

Les données de test sont d'abord :

交易ID	商品ID列表
T100	I1，I2，I5
T200	I2，I4
T300	I2，I3
T400	I1，I2，I4
T500	I1，I3
T600	I2，I3
T700	I1，I3
T800	I1，I2，I3，I5
T900	I1，I2，I3

TransactionID

ID du produitIDListe

T100

I1, I2, I5 td >

T200

I2, I4

T300

I2, I3

T400

I1, I2, I4

T500

I1, I3 td >

T600

I2, I3

T700

I1, I3

T800

I1, I2, I3, I5

T900

I1, I2, I3

Schéma des étapes de l'algorithme :

Comme vous pouvez le voir, le troisième tour d'ensembles de candidats s'est produit Considérablement réduit, pourquoi?

Veuillez noter les deux conditions de sélection des ensembles candidats :

1 Les deux conditions pour que deux ensembles d'éléments K soient connectés sont qu'ils aient K- 1. L'article est le même. Par conséquent, (I2, I4) et (I3, I5) ne peuvent pas être connectés. L’ensemble des candidats est restreint.

2. Si un ensemble d'éléments est un ensemble fréquent, alors il n'a pas d'ensemble fréquent qui ne soit pas un sous-ensemble. Par exemple, (I1, I2) et (I1, I4) obtiennent (I1, I2, I4), et le sous-ensemble (I1, I4) de (I1, I2, I4) n'est pas un ensemble fréquent. L’ensemble des candidats est restreint.

Les 2 ensembles candidats obtenus au troisième tour ont exactement l'appui égal à l'appui minimum. Par conséquent, ils sont tous inclus dans des ensembles fréquents.

Regardez maintenant l'ensemble des candidats et les résultats des ensembles fréquents du quatrième tour est vide

Vous pouvez voir que l'ensemble des candidats et l'ensemble fréquent est en fait vide ! Parce que les ensembles fréquents obtenus au troisième tour sont auto-connectés pour obtenir {I1, I2, I3, I5}, qui a le sous-ensemble {I2, I3, I5}, et {I2, I3, I5} n'est pas un ensemble fréquent, non Il satisfait à la condition selon laquelle un sous-ensemble d'ensembles fréquents est également un ensemble fréquent, il est donc coupé par élagage. Par conséquent, l'ensemble de l'algorithme est terminé et l'ensemble fréquent obtenu par le dernier calcul est pris comme résultat final de l'ensemble fréquent :

, c'est-à-dire : ['I1,I2,I3' , 'I1,I2,I5 ']

4. Code :

Écrivez du code Python pour implémenter l'algorithme Apriori. Le code doit prêter attention aux deux points suivants :

• Puisque l'algorithme Apriori suppose que les éléments de l'ensemble d'éléments sont triés par ordre lexicographique et que l'ensemble lui-même n'est pas ordonné, nous devons effectuer set et lister si nécessaire. Conversion ;
• Puisqu'un dictionnaire (support_data) est utilisé pour enregistrer la prise en charge de l'ensemble d'éléments, l'ensemble d'éléments doit être utilisé comme clé et l'ensemble de variables ne peut pas être utilisé comme clé. clé du dictionnaire, de sorte que l'ensemble d'éléments doit être converti en fixe au moment approprié. Collection Frozenset.

def local_data(file_path):    import pandas as pd

    dt = pd.read_excel(file_path)
    data = dt['con']
    locdata = []    for i in data:
        locdata.append(str(i).split(","))   # print(locdata)  # change to [[1,2,3],[1,2,3]]
    length = []    for i in locdata:
        length.append(len(i))  # 计算长度并存储
   # print(length)
    ki = length[length.index(max(length))]   # print(length[length.index(max(length))])  # length.index(max(length)读取最大值的位置，然后再定位取出最大值

    return locdata,kidef create_C1(data_set):    """
    Create frequent candidate 1-itemset C1 by scaning data set.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
    Returns:
        C1: A set which contains all frequent candidate 1-itemsets    """
    C1 = set()    for t in data_set:        for item in t:
            item_set = frozenset([item])
            C1.add(item_set)    return C1def is_apriori(Ck_item, Lksub1):    """
    Judge whether a frequent candidate k-itemset satisfy Apriori property.
    Args:
        Ck_item: a frequent candidate k-itemset in Ck which contains all frequent
                 candidate k-itemsets.
        Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
    Returns:
        True: satisfying Apriori property.
        False: Not satisfying Apriori property.    """
    for item in Ck_item:
        sub_Ck = Ck_item - frozenset([item])        if sub_Ck not in Lksub1:            return False    return Truedef create_Ck(Lksub1, k):    """
    Create Ck, a set which contains all all frequent candidate k-itemsets
    by Lk-1's own connection operation.
    Args:
        Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
        k: the item number of a frequent itemset.
    Return:
        Ck: a set which contains all all frequent candidate k-itemsets.    """
    Ck = set()
    len_Lksub1 = len(Lksub1)
    list_Lksub1 = list(Lksub1)    for i in range(len_Lksub1):        for j in range(1, len_Lksub1):
            l1 = list(list_Lksub1[i])
            l2 = list(list_Lksub1[j])
            l1.sort()
            l2.sort()            if l1[0:k-2] == l2[0:k-2]:
                Ck_item = list_Lksub1[i] | list_Lksub1[j]                # pruning
                if is_apriori(Ck_item, Lksub1):
                    Ck.add(Ck_item)    return Ckdef generate_Lk_by_Ck(data_set, Ck, min_support, support_data):    """
    Generate Lk by executing a delete policy from Ck.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
        Ck: A set which contains all all frequent candidate k-itemsets.
        min_support: The minimum support.
        support_data: A dictionary. The key is frequent itemset and the value is support.
    Returns:
        Lk: A set which contains all all frequent k-itemsets.    """
    Lk = set()
    item_count = {}    for t in data_set:        for item in Ck:            if item.issubset(t):                if item not in item_count:
                    item_count[item] = 1                else:
                    item_count[item] += 1
    t_num = float(len(data_set))    for item in item_count:        if (item_count[item] / t_num) >= min_support:
            Lk.add(item)
            support_data[item] = item_count[item] / t_num    return Lkdef generate_L(data_set, k, min_support):    """
    Generate all frequent itemsets.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
        k: Maximum number of items for all frequent itemsets.
        min_support: The minimum support.
    Returns:
        L: The list of Lk.
        support_data: A dictionary. The key is frequent itemset and the value is support.    """
    support_data = {}
    C1 = create_C1(data_set)
    L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
    Lksub1 = L1.copy()
    L = []
    L.append(Lksub1)    for i in range(2, k+1):
        Ci = create_Ck(Lksub1, i)
        Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
        Lksub1 = Li.copy()
        L.append(Lksub1)    return L, support_datadef generate_big_rules(L, support_data, min_conf):    """
    Generate big rules from frequent itemsets.
    Args:
        L: The list of Lk.
        support_data: A dictionary. The key is frequent itemset and the value is support.
        min_conf: Minimal confidence.
    Returns:
        big_rule_list: A list which contains all big rules. Each big rule is represented
                       as a 3-tuple.    """
    big_rule_list = []
    sub_set_list = []    for i in range(0, len(L)):        for freq_set in L[i]:            for sub_set in sub_set_list:                if sub_set.issubset(freq_set):
                    conf = support_data[freq_set] / support_data[freq_set - sub_set]
                    big_rule = (freq_set - sub_set, sub_set, conf)                    if conf >= min_conf and big_rule not in big_rule_list:                        # print freq_set-sub_set, " => ", sub_set, "conf: ", conf                        big_rule_list.append(big_rule)
            sub_set_list.append(freq_set)    return big_rule_listif __name__ == "__main__":    """
    Test    """
    file_path = "test_aa.xlsx"
  
    data_set,k = local_data(file_path)
    L, support_data = generate_L(data_set, k, min_support=0.2)
    big_rules_list = generate_big_rules(L, support_data, min_conf=0.4)    print(L)    for Lk in L:        if len(list(Lk)) == 0:            break
        print("="*50)        print("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport")        print("="*50)        for freq_set in Lk:            print(freq_set, support_data[freq_set])    print()    print("Big Rules")    for item in big_rules_list:        print(item[0], "=>", item[1], "conf: ", item[2])

Format de fichier :

test_aa.xlsx

name    con
T1     2,3,5T2     1,2,4T3     3,5T5     2,3,4T6     2,3,5T7     1,2,4T8     3,5T9     2,3,4T10    1,2,3,4,5

Recommandations d'apprentissage gratuites associées : python Tutoriel vidéo

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!