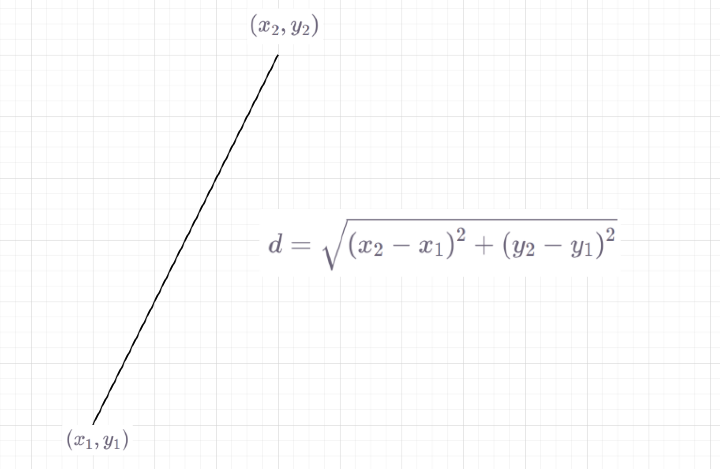Maison >développement back-end >C++ >Programme pour vérifier la similarité de deux triangles donnés
Programme pour vérifier la similarité de deux triangles donnés
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-08-25 17:33:03901parcourir
Dans cette question, nous apprendrons à vérifier la similitude de deux triangles donnés, ce qui présente de nombreux cas d'utilisation réels du point de vue d'un programmeur.
Pour créer et gérer des modèles d'objets 2D et 3D, vous devez utiliser des systèmes de CAO, l'une des fonctionnalités clés est la possibilité de comparer deux triangles.
Par exemple, les ingénieurs travaillant sur la conception et la construction devront peut-être faire correspondre les mesures des fondations du bâtiment aux plans. Les ingénieurs peuvent rapidement évaluer si les angles et les côtés d'une fondation correspondent à la disposition à l'aide d'outils de CAO, dotés de fonctionnalités intégrées permettant de vérifier la similitude de deux triangles. Cela contribue à garantir la stabilité structurelle et la sécurité du bâtiment.
De plus, le modèle 3D de l'objet est réalisé à l'aide d'un logiciel de CAO grâce à la technologie d'impression 3D. Pour garantir que le modèle est imprimé avec précision et dans les proportions souhaitées dans ce cas, un contrôle de similarité peut être utile. Ceci est essentiel pour les modèles complexes, car la validation manuelle des similarités peut être fastidieuse et sujette aux erreurs.
Les programmeurs dans le domaine de la robotique peuvent garantir la précision des mouvements du robot en utilisant des outils de vérification de similarité. Vérifier la similarité de deux triangles permet de garantir que les mouvements complexes effectués par les bras robotiques (souvent dotés de plusieurs articulations) sont précis et constants.
Instructions
Comprenons maintenant certaines des mathématiques impliquées dans le calcul de la similarité des triangles.
Deux triangles sont semblables s'ils ont les caractéristiques suivantes -
Les angles intérieurs de deux triangles sont égaux.
Les côtés correspondants d'un triangle ont les mêmes proportions.
Il existe trois méthodes pour déterminer si deux triangles sont similaires : SSS, SAS et AA. Discutons brièvement de chaque théorème.
Norme SSS (Side-Side-Side)
Dans deux triangles donnés, deux triangles sont semblables si les proportions des trois paires de côtés sont les mêmes.
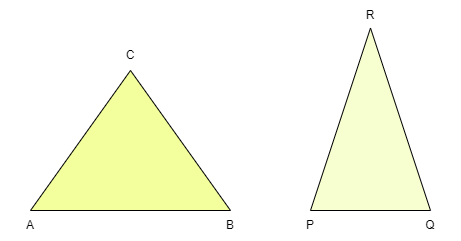
Considérons les deux triangles donnés ci-dessus. Si les proportions des trois côtés opposés sont égales, les deux triangles ci-dessus peuvent être similaires selon la norme SSS, c'est-à-dire AC/PR = AB/PQ = CB/RQ
Norme SAS (Side-Angle-Side)
Dans deux triangles donnés, deux triangles sont semblables si les proportions des deux paires de côtés sont les mêmes et que l'angle entre les deux côtés des deux triangles est le même.
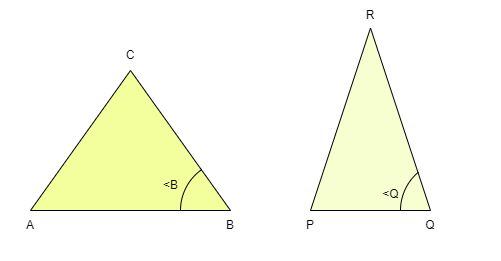
En prenant le triangle ci-dessus comme exemple, si AB/PQ = BC/QR et
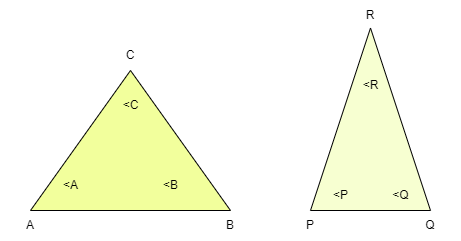
Norme AA (angle-angle)
Dans deux triangles donnés, si deux angles des deux triangles sont égaux, alors les deux triangles sont similaires.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Comment obtenir un résultat à virgule flottante à partir d'une division entière en C sans modifier les variables entières ?
- Utilisez l'addition ou la soustraction pour obtenir le nombre minimum d'étapes pour N à chaque étape
- Un guide pour diagnostiquer et réparer les fuites de mémoire dans les grandes applications C++
- Comment parcourir efficacement une liste d'arguments de modèle variadique compressée ?
- Les fonctions Consteval peuvent-elles activer la dépendance des paramètres de modèle sur les arguments de fonction en C 20 ?