Maison >développement back-end >C++ >Utilisez l'addition ou la soustraction pour obtenir le nombre minimum d'étapes pour N à chaque étape
Utilisez l'addition ou la soustraction pour obtenir le nombre minimum d'étapes pour N à chaque étape
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-09-16 13:13:22742parcourir
À partir de l'énoncé du problème ci-dessus, notre tâche est d'obtenir le nombre minimum d'étapes dans chacune desquelles nous pouvons obtenir le nombre N donné en utilisant l'addition ou la soustraction. Nous pouvons comprendre que nous devons imprimer le nombre minimum d'étapes pouvant être effectuées et l'ordre des étapes pour tout entier N donné, en ajoutant et en soustrayant les numéros d'étape pour arriver à un nombre commençant à 0.
Dans cet ensemble de problèmes, nous pouvons ajouter ou soustraire un nombre égal au nombre d'étapes jusqu'à la position actuelle à chaque étape. Par exemple, nous pouvons ajouter 1 ou -1 à l'étape 1. De plus, nous pouvons ajouter 2 ou -2 à l'étape 2 et ainsi de suite. Nous pouvons ajouter ou soustraire des nombres à chaque étape en fonction de la situation.
Le principal défi de ce problème est que nous devons effectuer le nombre minimum d'étapes en partant de 0 pour atteindre N. Comprenons mieux ce problème avec un exemple.
L'exemple ci-dessous vous montrera tous les nombres que nous pouvons obtenir en 2 étapes à partir de 0 en effectuant les opérations ci-dessus.
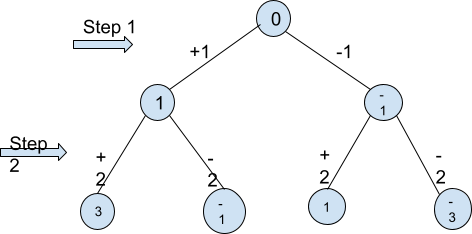
Par exemple, supposons que nous ayons N=1.
Sortie
Minimum no of steps: 1 Sequence of steps: 1
Instructions
Nous pouvons atteindre 1 de deux manières -
Ajoutez simplement 1 à l'étape 1 pour passer de 0 à 1, ce qui prend 1 étape.
Soustrayez 1 à l'étape 1 pour passer de 0 à -1, puis ajoutez 2 à l'étape 2 pour passer de -1 à 1, ce qui prend 2 étapes.
Puisque la question indique que nous avons besoin du nombre minimum d'étapes pour atteindre n'importe quel nombre N, la sortie souhaitée pour cette entrée sera 1.
Pour, N=3
Sortie
Minimum no of steps: 2 Sequence of steps: 1 2
Instructions
On ajoute 1 à l'étape 1 pour passer de 0 à 1, puis on ajoute 2 à l'étape 2 pour passer de 1 à 3.
Méthode
La meilleure façon de résoudre le problème est d’abord de déterminer si N est positif ou négatif. Nous devons respectivement ajouter ou soustraire le nombre approprié d’étapes pour résoudre le problème.
Si N est un nombre positif, continuez à ajouter des étapes jusqu'à ce que la somme soit supérieure ou égale à N.
De même, si N est négatif, continuez à soustraire le nombre de pas jusqu'à ce que la somme soit supérieure ou égale à N.
Si la somme est égale à N dans le cas ci-dessus, renvoie le nombre d'étapes et l'ordre des étapes. Le principal problème est de gérer la situation lorsque N est dépassé.
Une fois que la somme dépasse N, vérifiez si (somme-N) est paire ou impaire.
-
Si (somme-N) est paire, alors nous devons effectuer une soustraction par étapes de (somme-N)/2 pour atteindre N.
Comprenons mieux ce cas avec un exemple approprié.
Pour, N=8
1+2+3+4=10, ce qui est supérieur à 8.
Parce que 10-8=2 est un nombre pair. Nous allons donc soustraire par pas de 2/2, soit
Étape 1. L'ordre des étapes sera donc -1 2 3 4 et le minimum
Le nombre d'étapes pour atteindre N sera de 4.
-
Si (somme-N) est un nombre impair, déterminez d'abord si le nombre dont la somme dépasse N à l'étape précédente est pair ou impair.
Si l'étape précédente était impaire, effectuez une étape en ajoutant le numéro de l'étape suivante qui rendra notre (somme-N) paire, puis effectuez les étapes ci-dessus pour obtenir le résultat souhaité.
Par exemple, N=9
1+2+3+4=10, ce qui est supérieur à 9.
Parce que 10-9=1, c'est un nombre impair. L'étape suivante est 5, qui est un nombre impair, nous faisons donc simplement une étape et ajoutons 5 à la somme pour obtenir 15, ce qui fait (somme-N)=6. Effectuer la soustraction à l'étape 3 vous donnera la séquence 1 2 -3 4 5, qui est le résultat souhaité.
Supposons que l'étape précédente soit un nombre pair, dans ce cas, nous devons effectuer deux étapes, ajouter la i-ème étape et soustraire l'étape (i+1) pour obtenir (somme-N) sous forme de nombre pair pour obtenir la séquence d’étapes souhaitée.
Pour N=5
1+2+3=6, plus de 5.
Puisque (somme-N) =1, nous considérerons la dernière étape lorsque su dépasse le nombre N. Puisqu'il s'agit d'un nombre pair, nous effectuerons deux étapes, l'étape 4 et l'étape 5. Notre tâche est de faire (somme-N) quand même, en ajoutant à l'étape 4 et en soustrayant à l'étape 5, nous pouvons faire (somme-N) même si 1 est soustrait de la somme. Puisque (somme-N) est égale à 0, on obtient N. Par conséquent, la séquence est 1 2 3 4 -5.
Exemple
Voici le code C++ de la méthode -
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
vector <int> steps; // for storing the sequence
int totalSum=0;
int temp=0;
if(n>=0){ // if n is positive then temp will store positive
temp=1;
} else {
temp=-1; // n is negative then temp will store negative
}
n=abs(n);
int step=0;
for(step=1;totalSum<n;step++){ // for storing the steps till sum is not greater than n
steps.push_back(temp*step);
totalSum=totalSum+step;
}
if(totalSum>temp*n) { //when sum greater than n
if(step%2==0) { //when step is even
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the addition of next step
steps.push_back((temp*-1)*(step+1)); // store the subtraction of next step
totalSum--; //make totalSum even
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
} else { //when step is odd
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the next addition value
totalSum+=step;
step++;
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
}
}
//print the minimum number of steps taken
cout<<"The minimum number of steps : "<<steps.size()<<endl;
//print the steps is stored in vector
cout<<"Sequence of steps : ";
for(int i=0;i<steps.size();i++){
cout<<steps[i]<<" ";
}
}
int main(){
int m=17;
minimumStep(m);
return 0;
}
Sortie
The minimum number of steps : 6 Sequence of steps : 1 -2 3 4 5 6
Complexité temporelle : O(sqrt(N))
Complexité spatiale : O(sqrt(N))
Conclusion
Dans cet article, nous essayons d'expliquer la méthode pour trouver le nombre minimum d'étapes pour atteindre N en ajoutant ou en soustrayant à chaque étape et en imprimant la séquence. J'espère que cet article vous aidera à mieux apprendre ce concept.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Erreur de compilation C++ : Un fichier d'en-tête est référencé plusieurs fois, comment le résoudre ?
- Erreur de compilation C++ : paramètres de fonction incorrects, comment y remédier ?
- Erreur C++ : Le constructeur doit être déclaré dans l'espace public, comment y faire face ?
- Gestion des processus et synchronisation des threads en C++
- Comment gérer les problèmes de fractionnement des données dans le développement C++

