Maison >Périphériques technologiques >IA >Modèle de quota Duxiaoman basé sur une inférence causale contrefactuelle
Modèle de quota Duxiaoman basé sur une inférence causale contrefactuelle
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-06-03 22:16:021778parcourir
1. Paradigme de recherche sur l'inférence causale cadre de sortie potentiel

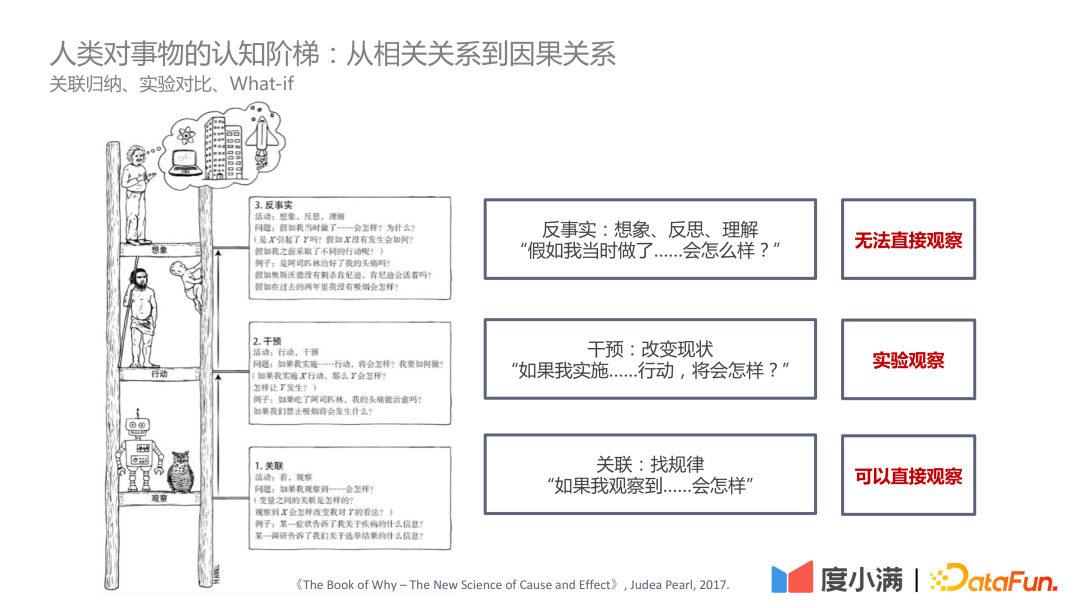
Dans le livre "The Book of Why – The New Science of Cause and Effect" de Judea Pearl, l'échelle cognitive se positionne sur trois niveaux :
- Le premier niveau - corrélation : découvrez les règles grâce à la corrélation, qui peuvent être directement observées
- Le deuxième niveau - intervention : si le statu quo est modifié, quelles actions doivent être mises en œuvre et quelles conclusions peuvent être tirées, vous pouvez Observation expérimentale
- Tout d'abord, expliquons les quatre manières de générer des corrélations :
- 1 Corrélation causale
- : Il existe une dépendance fiable, traçable et positive entre la cause et le résultat. . Les relations, telles que la fumée et les avertisseurs de fumée, sont liées de manière causale :
- 2. Corrélations confuses : Contient des variables confusionnelles qui ne peuvent pas être directement observées, telles que la question de savoir si la taille et la capacité de lecture peuvent être liées, ainsi que l'âge. doit être contrôlé Les variables sont similaires, tirant ainsi des conclusions valables
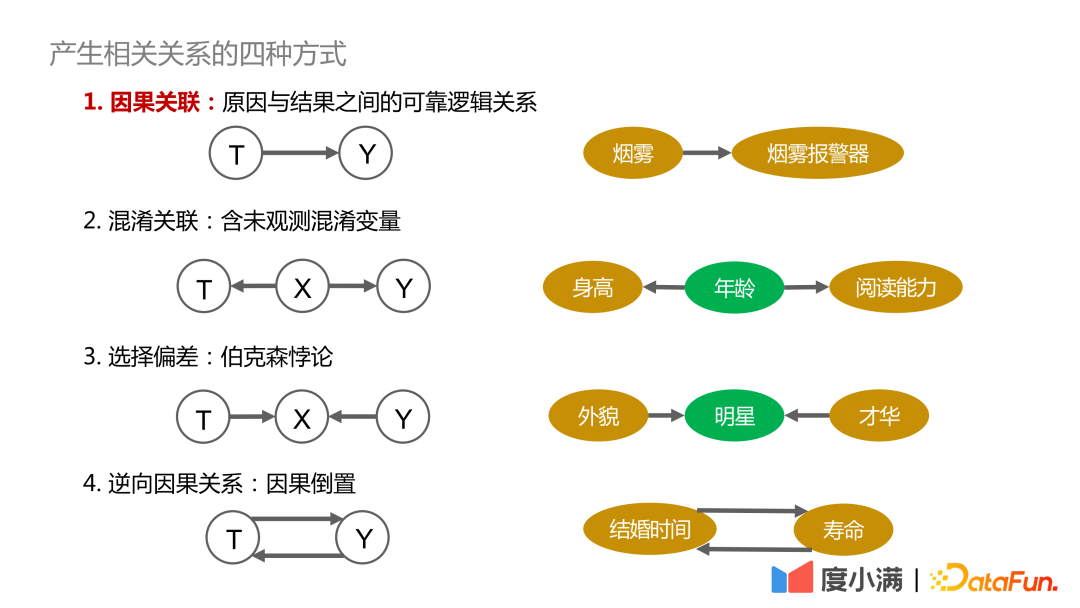
: C'est essentiellement le paradoxe de Berkson, comme l'exploration de la relation entre l'apparence et le talent, s'il est seulement observé parmi les stars. groupes, on pourrait en conclure que l’apparence et le talent ne font pas bon ménage. Si on l’observe chez tous les humains, il n’y a pas de relation causale entre l’apparence et le talent.
4. Causalité inversée: C'est-à-dire l'inversion de la cause et de l'effet. Par exemple, les statistiques montrent que plus les humains sont mariés longtemps, plus leur durée de vie est longue. Mais à l’inverse, on ne peut pas dire : si vous voulez vivre plus longtemps, vous devez vous marier tôt.
Comment les facteurs de confusion affectent les résultats d'observation, voici deux cas pour illustrer :
L'image ci-dessus décrit la relation entre le volume d'exercice et les niveaux de cholestérol. D’après l’image de gauche, nous pouvons conclure que plus on fait d’exercice, plus le taux de cholestérol est élevé. Cependant, lorsque la stratification par âge est ajoutée, sous la même stratification par âge, plus la quantité d'exercice est importante, plus le taux de cholestérol est bas. De plus, à mesure que nous vieillissons, les taux de cholestérol augmentent progressivement, cette conclusion est donc cohérente avec nos connaissances.
Le deuxième exemple est le scénario du crédit. Il ressort des statistiques historiques que plus la limite donnée (le montant d’argent pouvant être emprunté) est élevée, plus le taux de retard est bas. Cependant, dans le domaine financier, la qualification de crédit de l'emprunteur sera d'abord jugée sur la base de sa carte A. Si la qualification de crédit est meilleure, la plateforme accordera une limite plus élevée et le taux global de retard sera très faible. Cependant, des expériences aléatoires locales montrent que pour les personnes ayant les mêmes qualifications de crédit, il y aura certaines personnes dont la courbe de migration de la limite de crédit changera relativement lentement, et il y aura également des personnes dont le risque de migration de la limite de crédit sera plus élevé, c'est-à-dire après le crédit. La limite est augmentée, l'augmentation du risque sera plus importante.
Les deux cas ci-dessus illustrent que si les facteurs de confusion sont ignorés dans la modélisation, des conclusions erronées, voire opposées, peuvent être obtenues.
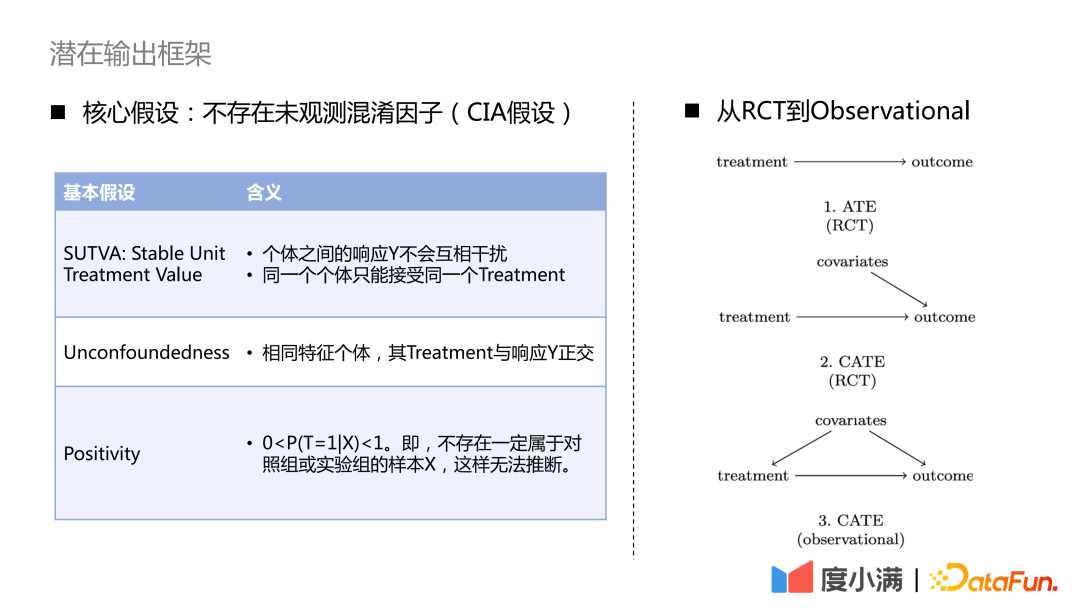
Comment passer des échantillons aléatoires ECR à la modélisation causale des échantillons observationnels ?
Pour le cas des échantillons RCT, si vous souhaitez évaluer l'indicateur ATE, vous pouvez utiliser la soustraction de groupe ou DID (différence de différence). Si vous souhaitez évaluer l'indicateur CATE, vous pouvez utiliser la modélisation ascendante. Les méthodes courantes incluent le méta-apprenant, le double apprentissage automatique, la forêt causale, etc. Il y a trois hypothèses nécessaires à noter ici : SUTVA, absence de confusion et positivité. L’hypothèse de base est qu’il n’existe aucun facteur de confusion non observé.
Pour le cas où il n'y a que des échantillons d'observation, la relation causale entre traitement-> résultat ne peut pas être obtenue directement. Nous devons utiliser les moyens nécessaires pour couper le chemin dérobé des covariables au traitement. Les méthodes courantes sont les méthodes de variables instrumentales et l’apprentissage des représentations contrefactuelles. La méthode des variables instrumentales doit décortiquer les détails de l’entreprise spécifique et tracer un diagramme de cause à effet des variables commerciales. L'apprentissage des représentations contrefactuelles repose sur un apprentissage automatique mature pour faire correspondre des échantillons avec des covariables similaires à des fins d'évaluation causale.
2. L'évolution du cadre d'inférence causale
1. Des données aléatoires aux données observées
Ensuite, nous présenterons l'évolution du cadre d'inférence causale, et comment pour passer à l'apprentissage de la représentation causale étape par étape.
Les modèles Uplift courants incluent : Slearner, Tlearner, Xlearner.
où Slearner traite les variables intermédiaires comme des caractéristiques unidimensionnelles. Il convient de noter que dans les modèles d’arbres courants, le traitement est facilement dépassé, ce qui entraîne des estimations plus faibles de l’effet du traitement.
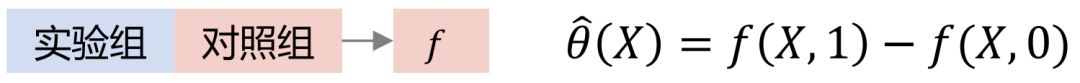
Tlearner discrétise le traitement, modélise les variables intermédiaires en groupes, construit un modèle de prédiction pour chaque traitement, puis fait une différence. Il est important de noter que des échantillons de plus petite taille conduisent à des variances estimées plus élevées.
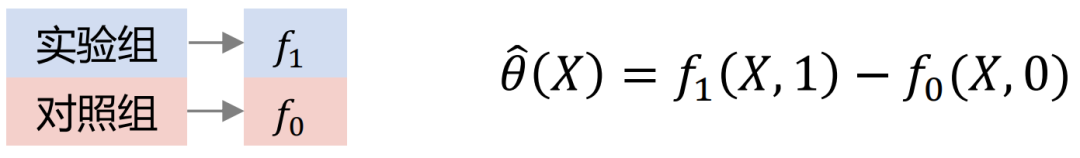
Modélisation croisée du groupe Xlearner, le groupe expérimental et le groupe témoin sont calculés de manière croisée et formés séparément. Cette méthode combine les avantages de l'apprenant S/T, mais son inconvénient est qu'elle introduit des erreurs de structure de modèle plus élevées et augmente la difficulté d'ajustement des paramètres.
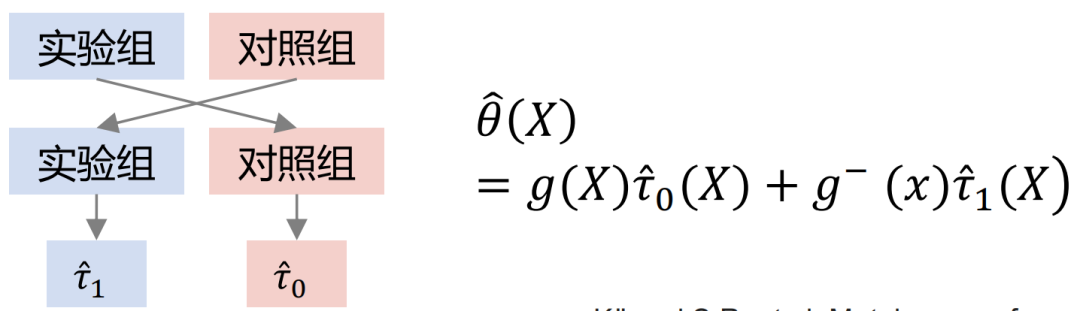
Comparaison de trois modèles :
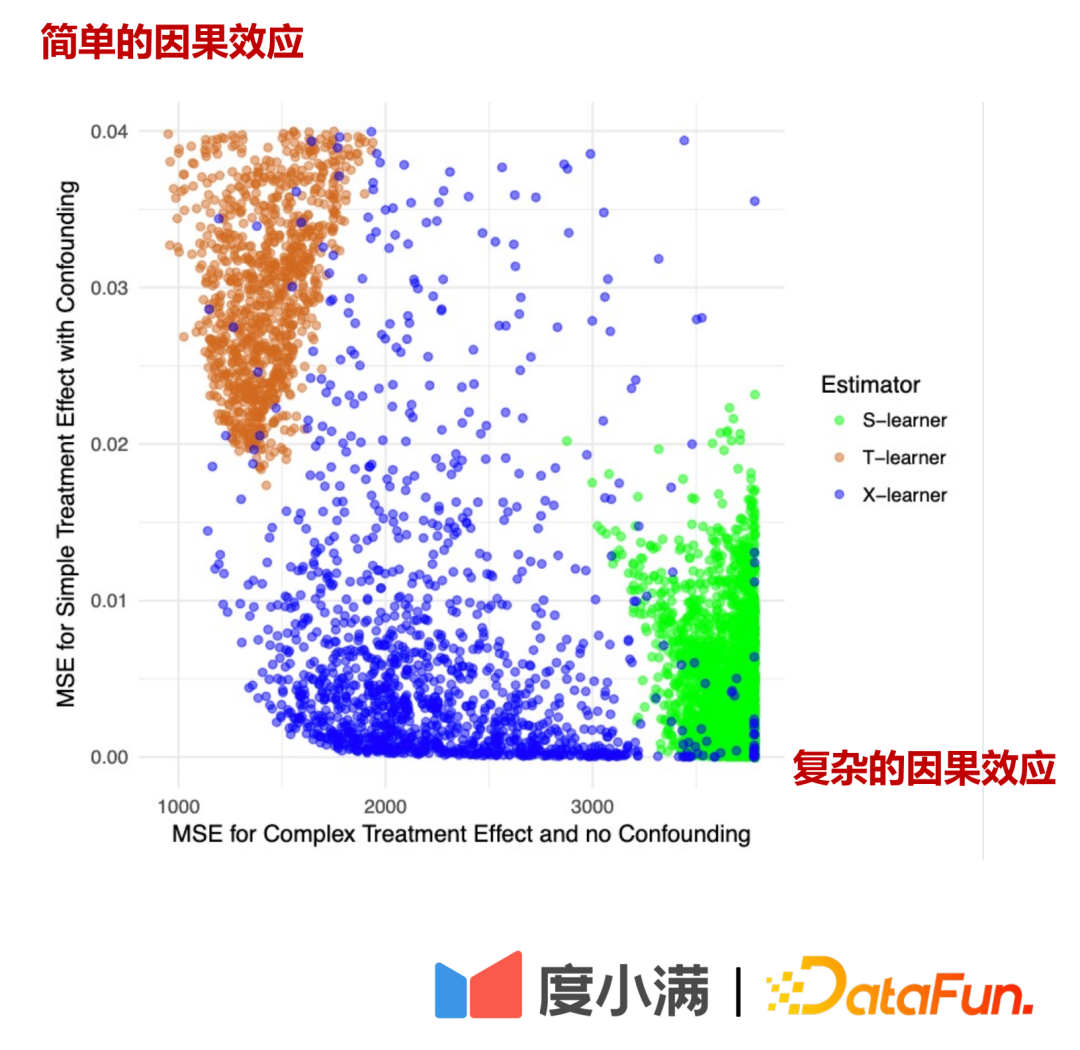
Dans la figure ci-dessus, l'axe horizontal est l'effet causal complexe, l'erreur d'estimation de MSE, et l'axe vertical est Effet de causalité simple, l'axe horizontal et l'axe vertical représentent respectivement deux éléments de données. Le vert représente la distribution des erreurs de Slearner, le marron représente la distribution des erreurs de Tlearner et le bleu représente la distribution des erreurs de Xlearner.
Dans des conditions d'échantillonnage aléatoire, Xlearner est meilleur pour l'estimation d'effet causal complexe et l'estimation d'effet causal simple ; Slearner est relativement médiocre pour l'estimation d'effet causal complexe et est meilleur pour l'estimation d'effet causal simple ;
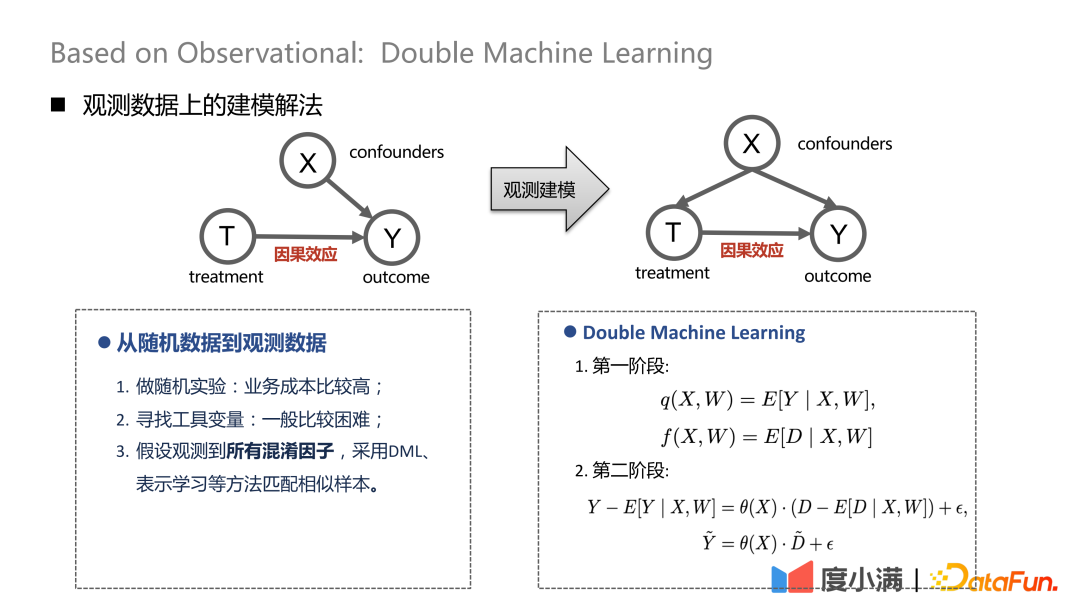
S'il y a des échantillons aléatoires, les flèches de X à T peuvent être supprimées. Après le passage à la modélisation observationnelle, les flèches de X à T ne peuvent pas être supprimées. Le traitement et les résultats seront affectés en même temps par les facteurs confondants. À ce stade, un certain traitement de dépolarisation peut être effectué. Par exemple, la méthode DML (Double Machine Learning) effectue une modélisation en deux étapes. Dans la première étape, X voici les propres caractéristiques de représentation de l’utilisateur, telles que l’âge, le sexe, etc. Les variables confusionnelles pourraient inclure, par exemple, les efforts historiques visant à éliminer des groupes spécifiques de personnes. Dans la deuxième étape, l'erreur sur le résultat du calcul de l'étape précédente est modélisée, voici l'estimation de CATE.
Il existe trois méthodes de traitement des données aléatoires aux données d'observation :
(1) Faire des expériences aléatoires, mais le coût commercial est plus élevé
(2) Trouver des variables instrumentales ; , généralement Relativement difficile ;
(3) Supposons que tous les facteurs de confusion sont observés et utilisez le DML, l'apprentissage des représentations et d'autres méthodes pour faire correspondre des échantillons similaires.
2. Apprentissage de la représentation causale
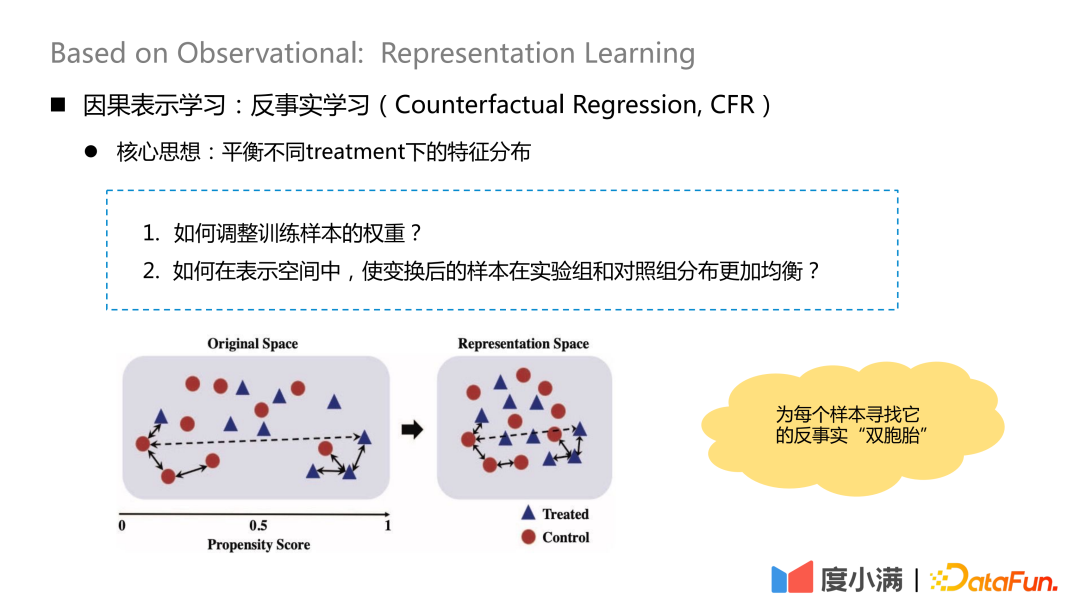
L'idée centrale de l'apprentissage contrefactuel est d'équilibrer la distribution des caractéristiques sous différents traitements.
Il y a deux questions principales :
1 Comment ajuster le poids des échantillons d'entraînement ?
2. Comment répartir plus uniformément les échantillons transformés dans le groupe expérimental et le groupe témoin dans l'espace de représentation ?
L'idée essentielle est de trouver son "jumeau" contrefactuel pour chaque échantillon après cartographie de transformation. Après cartographie, la distribution de X dans le groupe de traitement et le groupe témoin est relativement similaire.
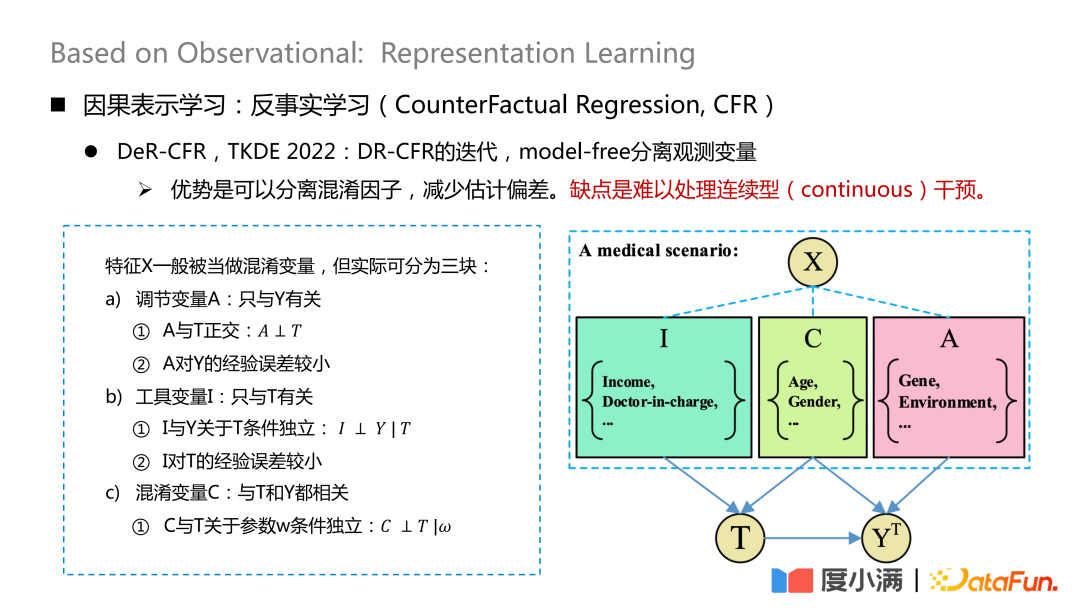
Le travail le plus représentatif est un article publié sur TKDE 2022, qui présente certains travaux de DeR-CFR. Cette partie est en fait une itération du modèle DR-CRF, utilisant une méthode de séparation sans modèle. variables observées.
Divisez la variable X en trois parties : la variable d'ajustement A, la variable instrumentale I et la variable de confusion C. Ensuite, I, C et A sont utilisés pour ajuster le poids de X sous différents traitements afin d'atteindre l'objectif de modélisation causale sur les données observées.
L'avantage de cette méthode est qu'elle peut séparer les facteurs de confusion et réduire les biais d'estimation. L’inconvénient est qu’il est difficile de gérer des interventions continues.
Le cœur de ce réseau est de savoir comment séparer les trois types de variables A/I/C. La variable d'ajustement A n'est liée qu'à Y, et il faut s'assurer que A et T sont orthogonaux, et l'erreur empirique de A à Y est faible, la variable instrumentale I n'est liée qu'à T, et elle doit satisfaire le ; indépendance conditionnelle de I et Y par rapport à T, et expérience de I par rapport à T L'erreur est faible ; la variable de confusion C est liée à la fois à T et Y, et w est le poids du réseau après avoir donné le réseau. poids, il faut s’assurer que C et T sont conditionnellement indépendants par rapport à w. L'orthogonalité ici peut être obtenue grâce à des formules de distance générales, telles que la perte de log ou la distance euclidienne mse et d'autres contraintes.
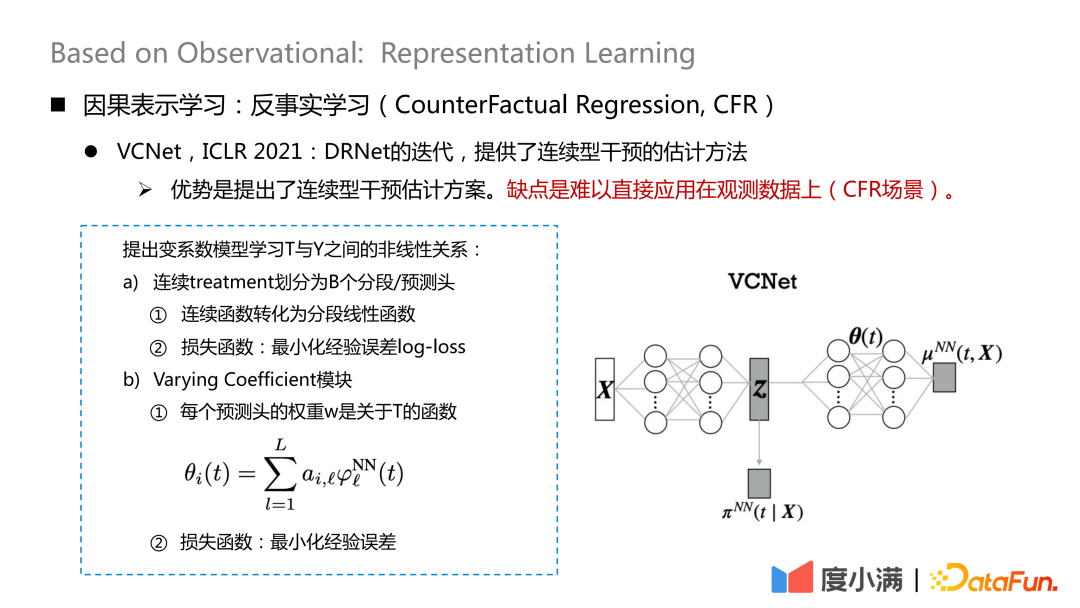
Il existe également de nouvelles études sur la manière de gérer l'intervention continue, publiées sur ICLR2021, qui fournissent une méthode d'estimation de l'intervention continue. L’inconvénient est qu’il est difficile de l’appliquer directement aux données d’observation (scénario CFR).
Map X sur Z. Z contient principalement les variables I et C dans la décomposition X mentionnée précédemment, c'est-à-dire que les variables qui contribuent au traitement sont extraites de X. Ici, le traitement continu est divisé en B têtes de segmentation/prédiction, et chaque fonction continue est convertie en une fonction linéaire segmentée pour minimiser la perte de log d'erreur empirique, qui est utilisée pour apprendre
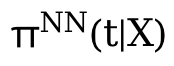
puis utilisez-le pour apprendre Complétez Z et θ(t) pour apprendre. 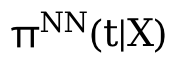
3. Modèle de crédit contrefactuel Mono-CFR
Enfin, présentons le modèle de crédit contrefactuel de Du Xiaoman. Le problème principal ici est de résoudre le problème de l'estimation contrefactuelle du traitement continu sur les données d'observation.
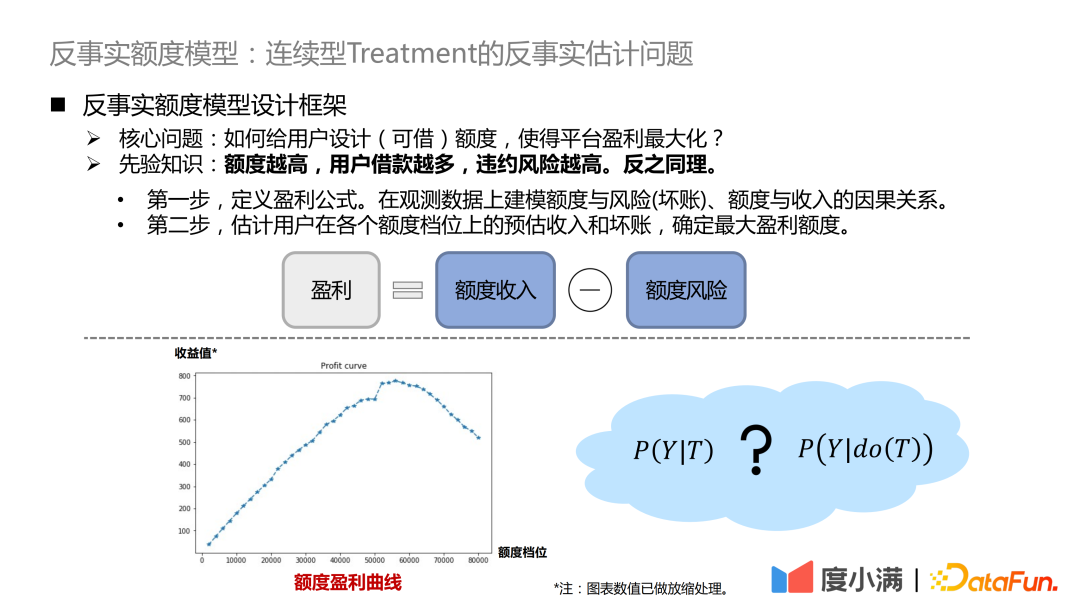
La question centrale est la suivante : comment concevoir un quota (empruntable) pour les utilisateurs afin de maximiser les profits de la plateforme ? La connaissance a priori ici est que plus la limite est élevée, plus les utilisateurs empruntent et plus le risque de défaut est élevé. Vice versa.
- La première étape consiste à définir la formule de profit. Bénéfice = revenu de quota - risque de quota. La formule paraît simple, mais en réalité il y a de nombreux détails à ajuster. De cette manière, le problème se transforme en modélisation de la relation causale entre le montant et le risque (créances douteuses), et le montant et le revenu sur les données d'observation.
- La deuxième étape consiste à estimer les revenus estimés et les créances irrécouvrables de l'utilisateur à chaque niveau de quota et à déterminer le montant maximum du profit.
Nous attendons de chaque utilisateur qu'il ait une courbe de profit comme le montre la figure ci-dessus et qu'il fasse des estimations contrefactuelles de la valeur des revenus à différents niveaux de quota.
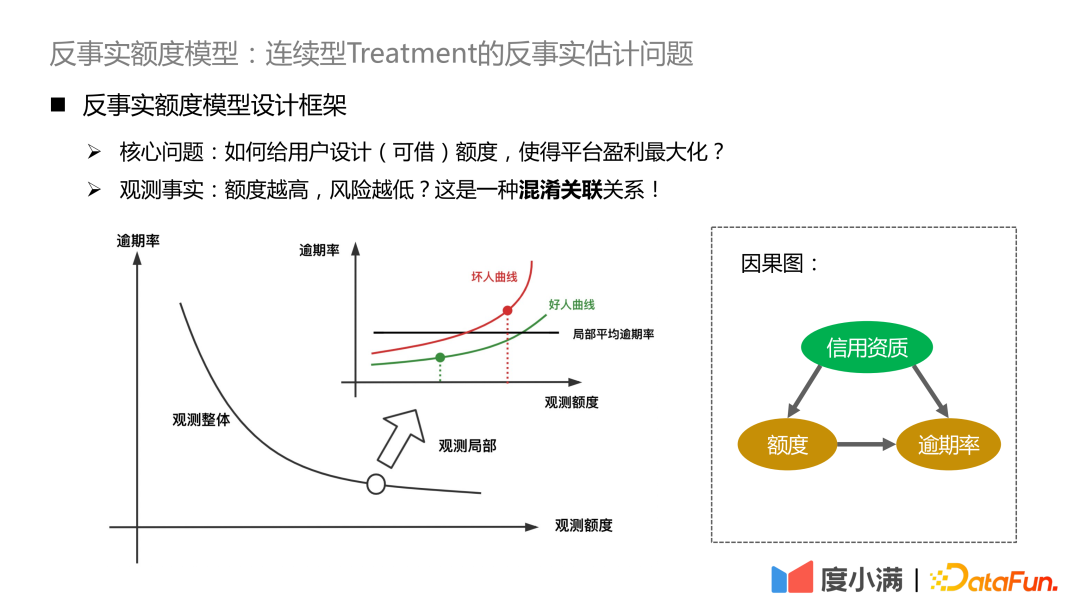
Si vous voyez dans les données d'observation que plus le montant est élevé, plus le risque est faible, essentiellement en raison de l'existence de facteurs confondants. Le facteur de confusion dans notre scénario concerne les qualifications créditées. Pour les personnes ayant de bonnes qualifications en matière de crédit, la plateforme accordera une limite plus élevée, et vice versa. Le risque absolu des personnes ayant d’excellentes qualifications en matière de crédit reste nettement inférieur à celui des personnes ayant de faibles qualifications en matière de crédit. Si vous améliorez vos qualifications de crédit, vous verrez que l'augmentation de la limite entraînera une augmentation du risque et que la limite supérieure dépassera la propre solvabilité de l'utilisateur.
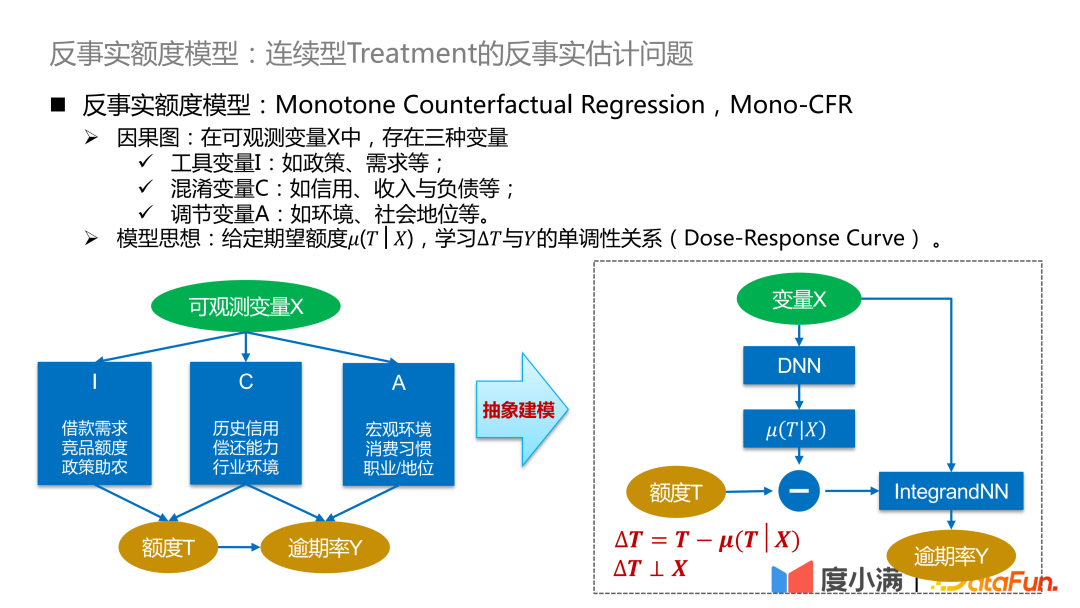
Nous commençons à présenter le cadre du modèle de crédit contrefactuel. Parmi les variables observables .
- Variable instrumentale I : telle que la politique, la demande, etc., qui affectera la stratégie de quota historique, mais n'affectera pas la probabilité de retard.
- Variables C déroutantes : telles que le crédit, le revenu et le passif, etc., qui affectent simultanément l'ajustement de la limite et la probabilité de retard de la personne.
- Ajustement de la variable A : telle que l'environnement, le statut social, etc., affectera le taux de retard.
Idée de modèle : étant donné la quantité attendue μ(T|X), apprenez la relation monotone entre ΔT et Y (courbe dose-réponse). La quantité attendue peut être comprise comme la quantité de tendance de continuité apprise par le modèle, de sorte que la relation entre la variable de confusion C et la quantité T puisse être déconnectée et convertie en l'apprentissage de la relation causale entre ΔT et Y, de manière à comparer la distribution. de Y sous ΔT Bonne caractérisation.
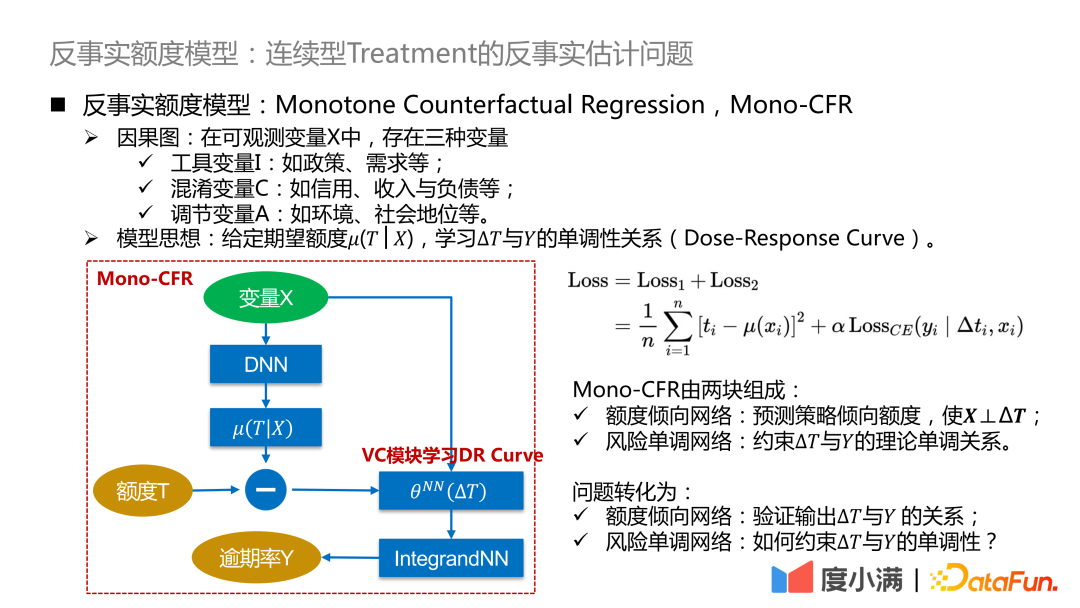
Le cadre abstrait ci-dessus est affiné ici : ΔT est converti en un modèle à coefficient variable, puis connecté au réseau IntegrandNN. L'erreur de formation est divisée en deux parties : .
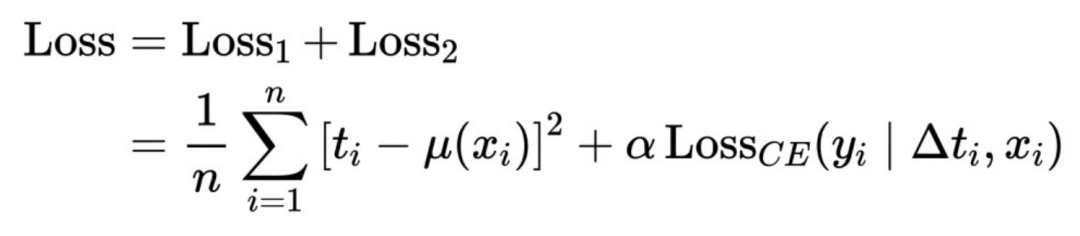
Le α ici est un hyperparamètre qui mesure l'importance du risque.
Mono-CFR se compose de deux parties :
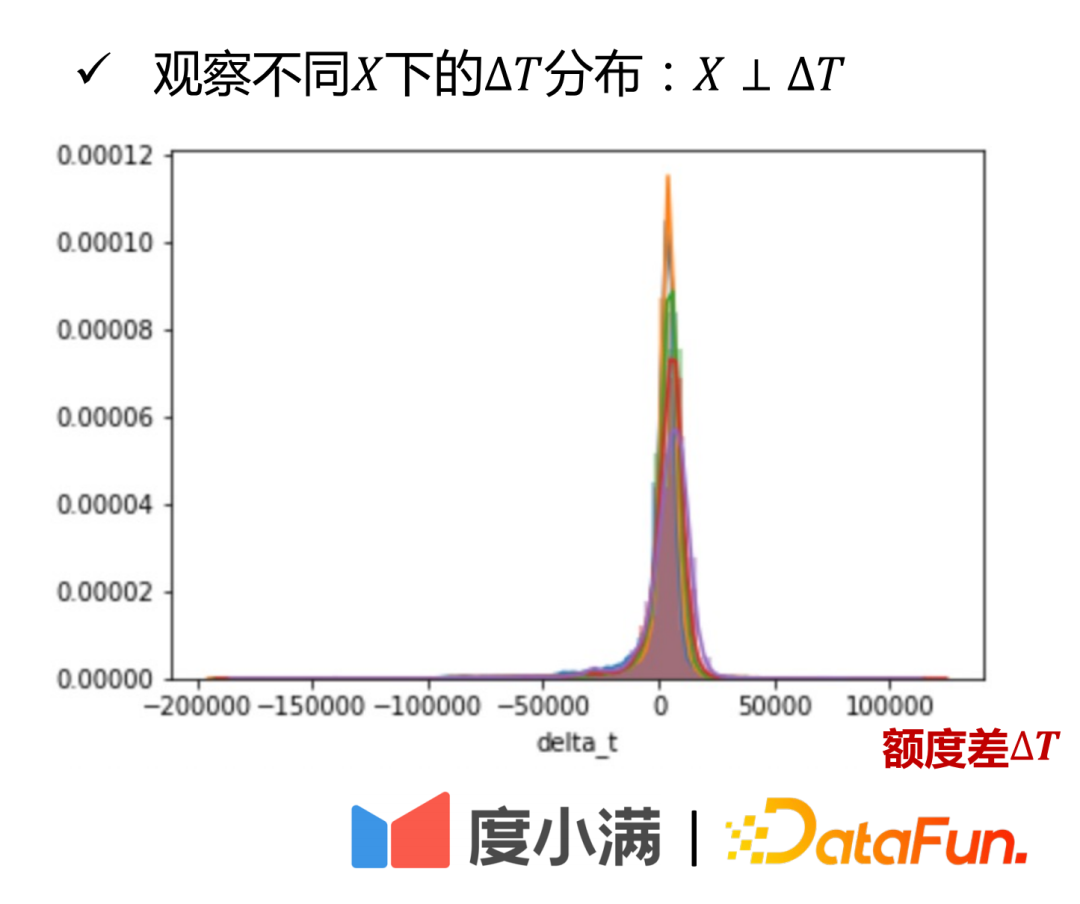
- Réseau de propension au montant : prédit le montant de la préférence stratégique, de sorte que X⊥ΔT.
Fonction 1 : Distiller les variables de X qui sont les plus pertinentes pour T et minimiser l'erreur empirique.
Fonction 2 : Ancrage d'échantillons approximatifs sur des stratégies historiques.
- Réseau monotone de risque : La relation monotone théorique entre la contrainte ΔT et Y.
Fonction 1 : Appliquer des contraintes monotones indépendantes aux variables à coefficients faibles.
Fonction 2 : Réduire les biais d'estimation.
Le problème se transforme en :
- Réseau de propension en montant : Vérifier la relation entre la sortie ΔT et Y.
- Réseau monotone de risque : Comment contraindre la monotonie de ΔT et Y ?
L'entrée réelle du réseau de propension au montant est la suivante :
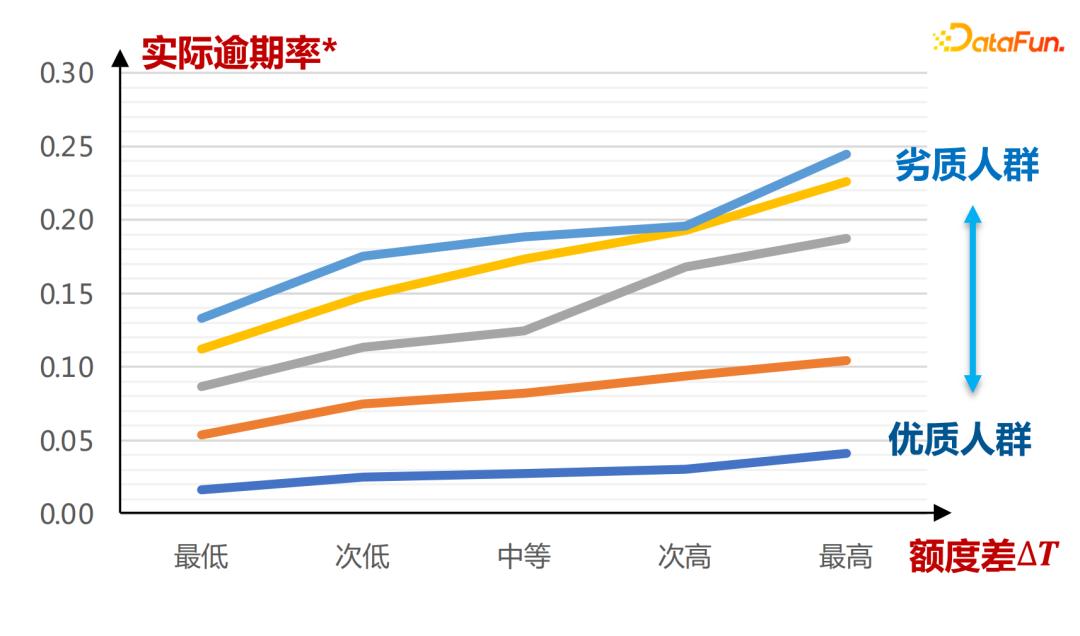
L'axe horizontal est le groupe défini par le score de la carte A. On peut voir que sous différents montants de propension. μ(T|X) , la différence de crédit ΔT et le taux de retard Y montrent une relation croissante monotone, plus la qualité est mauvaise, plus la courbe de variation de la différence de crédit ΔT est raide, la courbe de variation réelle du taux de retard est également plus raide et la pente de. toute la courbe est plus grande. Les conclusions ici sont entièrement tirées de l’apprentissage de données historiques.
Cela peut être vu sur le tableau de répartition de Ceci est expliqué d'un point de vue pratique.
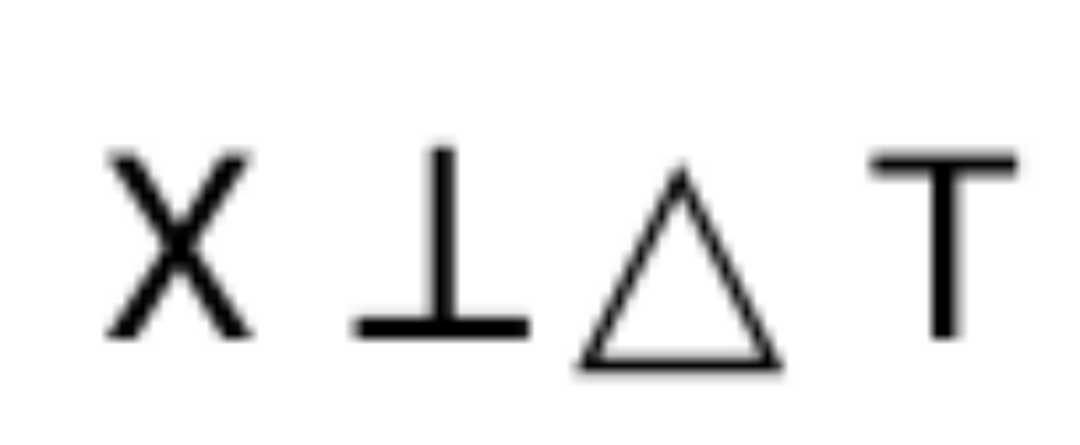
D'un point de vue théorique, cela peut aussi être rigoureusement prouvé.
La deuxième partie est la mise en œuvre du réseau monotone de risque :

L'expression mathématique de la fonction ELU+1 est ici :
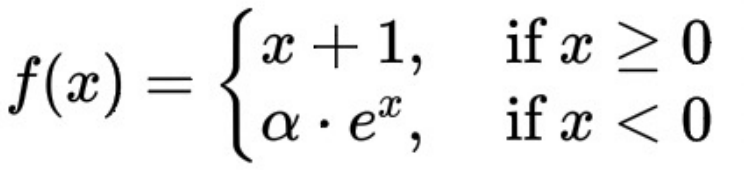
ΔT et le taux de retard affichent une tendance monotone à la hausse, qui est garantie par la dérivée de la fonction ELU+1 étant toujours supérieure ou égale à 0.
Ensuite, expliquez comment le réseau monotone du risque peut apprendre avec plus de précision pour les variables à coefficient faible :
Supposons qu'il existe une telle formule :
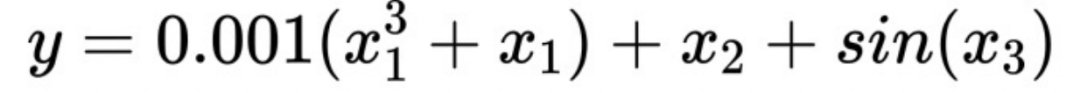
Vous peut voir ici x1 est une variable à coefficient faible. Lorsque des contraintes de monotonie sont imposées sur x1, l'estimation de la réponse Y est plus précise. Sans une telle contrainte distincte, l'importance de x1 sera submergée par x2, ce qui entraînera un biais accru du modèle.
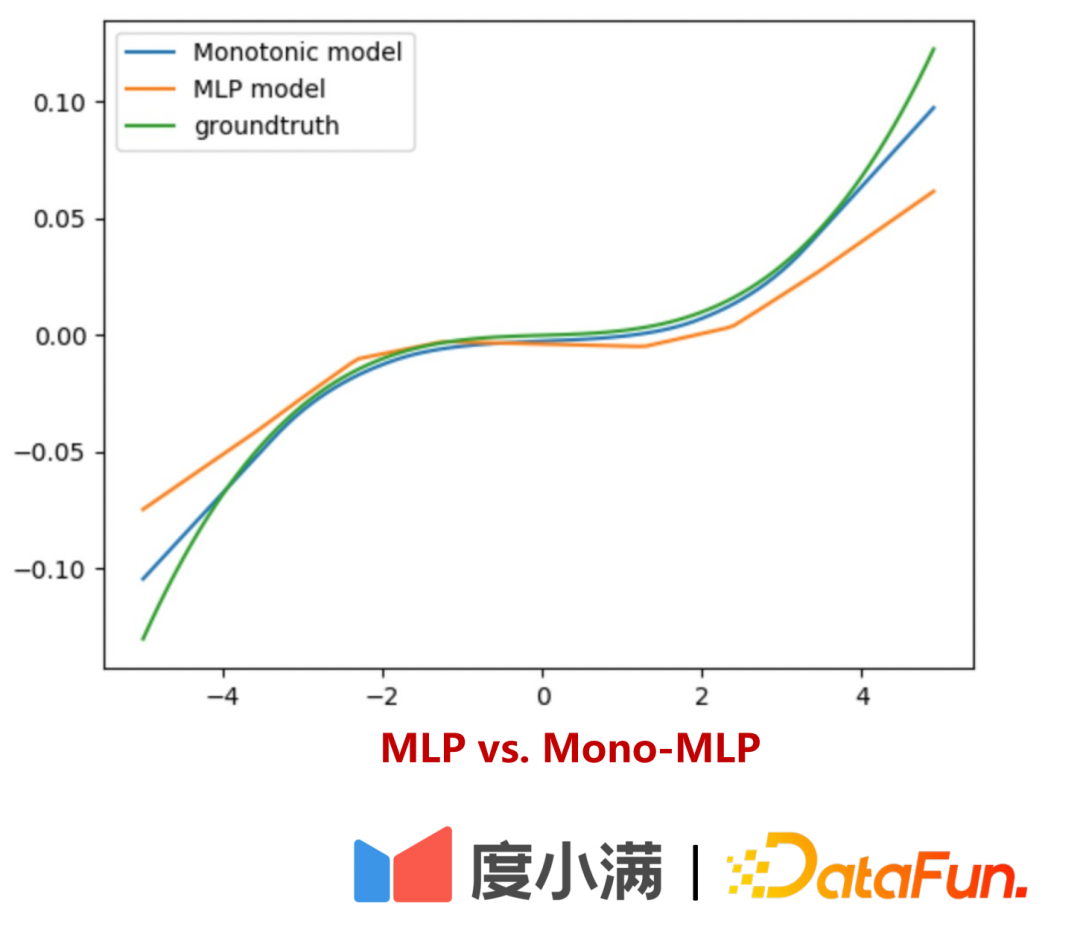
Comment évaluer la courbe d'estimation des risques du quota hors ligne ?
est divisé en deux parties :
- Première partie : Vérification interprétable
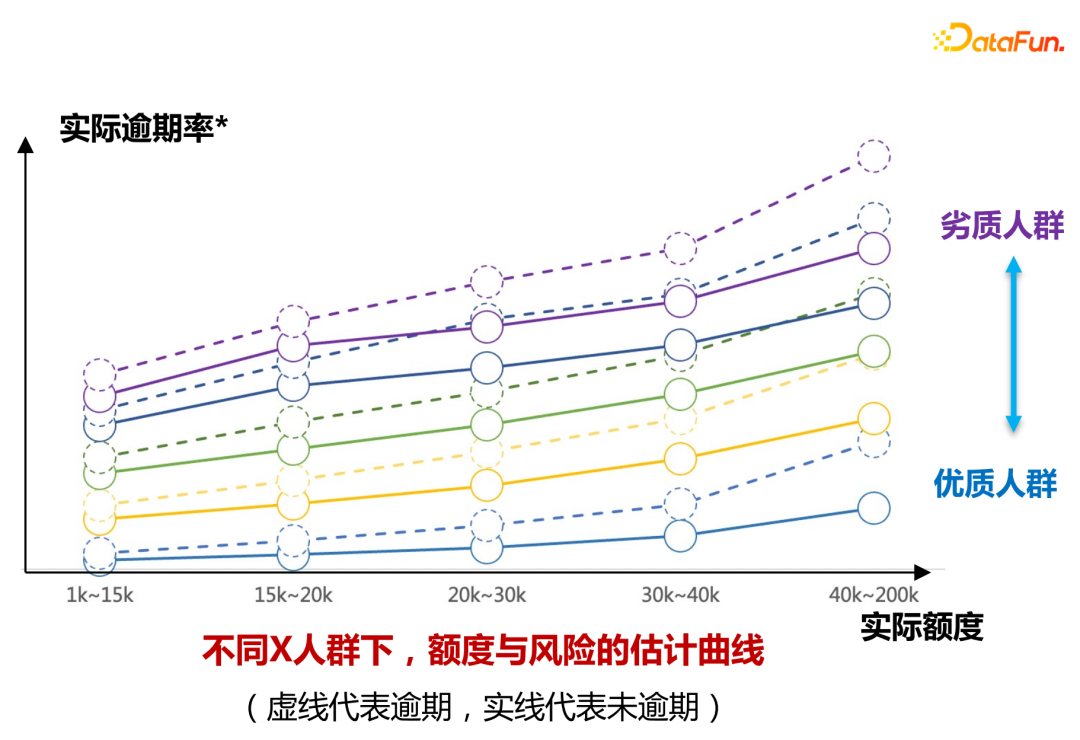
personnes ayant des qualifications différentes Dessinez la limite de risque comme indiqué dans la figure ci-dessus Grâce à la courbe de changement, le modèle peut apprendre la distinction entre le quota réel et le taux de retard de différents niveaux de personnes ayant différentes qualifications (marqués par différentes couleurs dans la figure).
- Partie 2 : Utilisez de petites expériences de trafic pour vérifier que l'écart de risque dans différentes plages d'augmentation de quota peut être obtenu grâce au regroupement ascendant.
Conclusion de l'expérience en ligne :
À condition que le quota augmente de 30 %, le montant des utilisateurs en retard diminue de plus de 20 %, les emprunts augmentent de 30 % et la rentabilité augmente de plus de 30%.
Attentes futures du modèle :
Séparez plus clairement les variables instrumentales et les variables modératrices sous une forme sans modèle, afin que le modèle puisse mieux fonctionner en matière de transfert de risque sur des groupes de mauvaise qualité.
Dans des scénarios commerciaux réels, le processus d'itération d'évolution du modèle de Du Xiaoman est le suivant :
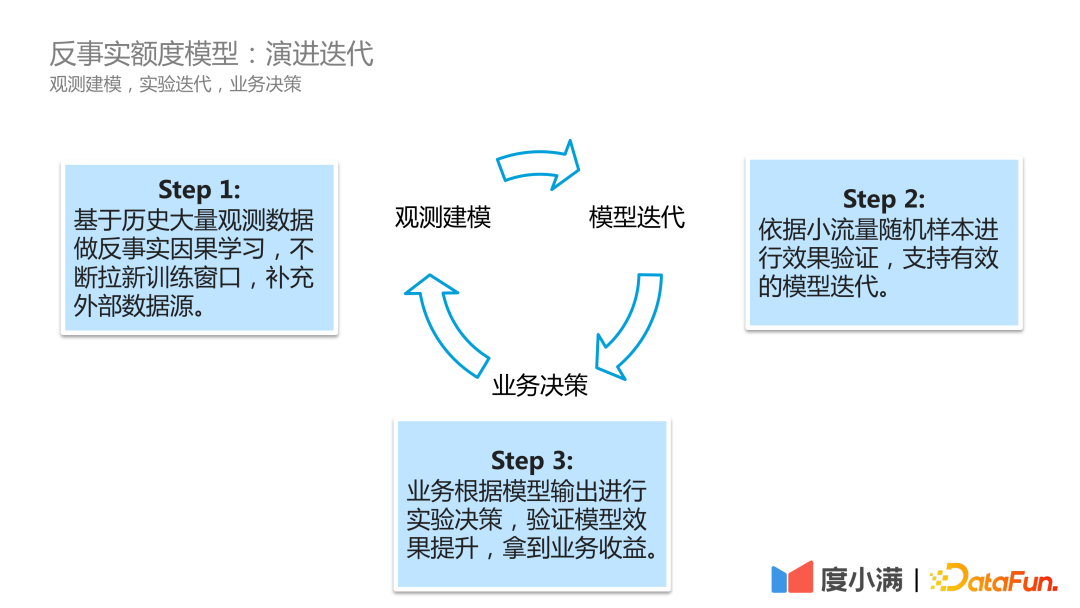
La première étape consiste à modéliser l'observation, à faire rouler en continu les données d'observation historiques, à effectuer un apprentissage causal contrefactuel, à ouvrir constamment de nouvelles fenêtres de formation et à compléter les sources de données externes.
La deuxième étape est l'itération du modèle. L'effet est vérifié sur la base d'échantillons aléatoires de petit trafic pour prendre en charge une itération efficace du modèle.
La troisième étape est la prise de décision commerciale. L'entreprise prend des décisions expérimentales basées sur les résultats du modèle pour vérifier l'amélioration de l'effet du modèle et obtenir des avantages commerciaux.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

