Exemple d'analyse des index et des algorithmes du moteur de stockage Mysql Innodb

1. Présentation

S'il y a trop peu d'index, l'efficacité des requêtes sera faible ; s'il y a trop d'index, les performances du programme seront affectées et l'utilisation des index doit être cohérente avec la situation réelle.
Innodb prend en charge les index, notamment :

• Recherche en texte intégral, à l'aide d'un index inversé

• Indice de hachage, adaptatif, sans intervention humaine, créé sur la base de la page d'index clusterisé dans le pool de tampons, et la table entière ne sera pas de hachage l'indexation est effectuée, donc l'indexation est très rapide.

• L'index arborescent B+, un index au sens traditionnel, est actuellement l'index le plus efficace et le plus couramment utilisé dans les bases de données relationnelles.

L'arbre B+ ne peut pas localiser l'enregistrement de ligne spécifique sur la table, mais renvoie la page où se trouve l'enregistrement de ligne ; enfin, il le localise avec précision dans la mémoire en fonction des informations d'emplacement et des informations d'enregistrement suivantes dans l'enregistrement de ligne ; en-tête.

2. Structure des données et algorithme

1. Recherche binaire

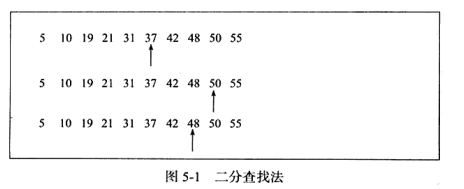
La recherche binaire ne peut être utilisée que pour rechercher un ensemble de données linéaires ordonnées. La valeur médiane est prise à chaque fois, en commençant par la plus petite valeur et en reculant avec la plus grande. valeur. La complexité temporelle pour trouver le nombre 48 dans un tableau ordonné est de log N, comme le montre la figure ci-dessous.

2. Arbre de recherche binaire et arbre binaire équilibré

1) Arbre de recherche binaire

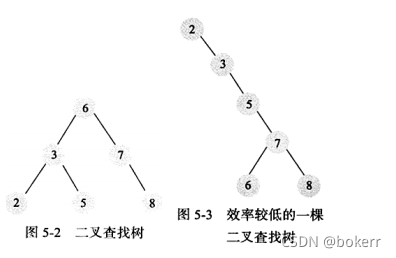
L'arbre de recherche binaire fait référence à un arbre binaire qui satisfait : le nœud enfant gauche de tout nœud est plus petit que lui-même, et tout nœud A un arbre binaire dont le nœud enfant droit est supérieur à lui-même est un arbre de recherche binaire.

Les arbres binaires ordinaires ne peuvent pas garantir le temps d'accès O(logN), car dans des cas extrêmes, ils peuvent même dégénérer en une liste chaînée.

Lorsqu'un ensemble de données ordonnées est construit afin de construire un arbre binaire, alors une liste chaînée est obtenue. À ce moment, la complexité temporelle devient : O(N)

2) Arbre binaire équilibré

. Arbre binaire équilibré et arbre binaire L'arbre de recherche de fork est similaire, mais ajoute une restriction : la hauteur des sous-arbres gauche et droit de chaque nœud diffère d'au plus 1. Lors du processus de construction d'un arbre binaire, si cette condition n'est pas respectée, elle peut être résolue par une rotation appropriée.

L'arbre binaire équilibré garantit une complexité temporelle de : O(logN)

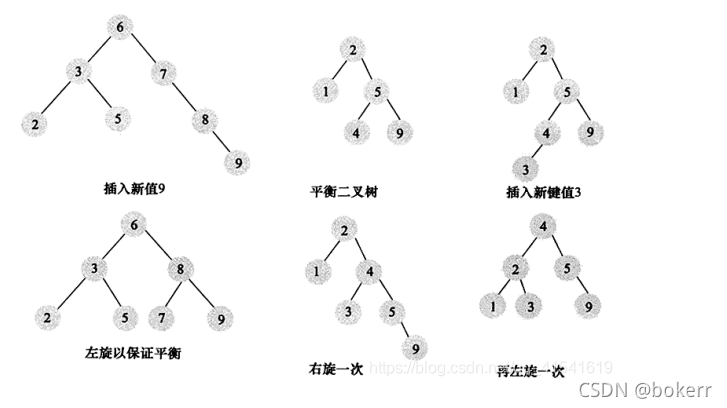
Bien qu'il puisse garantir un temps d'accès de O(logN), il n'est pas adapté à l'indexation de bases de données :

Lorsque la quantité de données est très grand , la hauteur d'un arbre binaire augmentera rapidement (par exemple, 1024 est égal à 2 élevé à la puissance 10), donc log(N) est également très significatif.

L'exécution d'E/S sur disque plusieurs fois est due au fait que les nœuds feuilles de l'arborescence binaire ne peuvent accueillir qu'un seul élément de données, ce qui est sa caractéristique la plus défavorable. Cependant, dans les applications réelles, les lectures fréquentes du disque seront désastreuses par rapport au temps nécessaire au processeur pour exécuter les instructions. Par conséquent, les arbres binaires ne conviennent pas à l’indexation de bases de données.

Pour les disques durs mécaniques, le temps d'accès dépend de la vitesse du disque et du temps de mouvement de la tête, qui sont tous complétés par la structure mécanique. Par rapport aux instructions de signaux électriques exécutées dans le CPU, la vitesse doit être très différente.

10 millions de données, si un arbre binaire équilibré est utilisé (la pire limite de temps est 1,44 * logN), même si la pire limite de temps n'est pas prise, le calcul final basé sur log(N) est d'environ 24, ce qui signifie que 24 E/S disque sont nécessaires, cela ne fonctionne évidemment pas.

[La hauteur de l'arbre est la valeur logarithmique arrondie, par exemple : log3 = 1,58, la hauteur de l'arbre est 2 ;]

3 Arbre B+

En raison des limitations des arbres binaires équilibrés, les arbres B+ ont besoin. à introduire.

L'arborescence B+ est un arbre de recherche équilibré spécialement conçu pour les disques ou autres périphériques auxiliaires à accès direct. Dans l'arborescence B+, tous les nœuds d'enregistrement sont stockés séquentiellement sur les nœuds feuilles de la même couche en fonction de la taille de la valeur clé de chacun. Les pointeurs de nœud feuille sont liés.

1. Définition complète de l'arbre B+

Un arbre B+ d'ordre M doit répondre aux propriétés suivantes :

Dans toutes les définitions suivantes, concernant la division de deux nombres, s'ils ne peuvent pas être divisés en nombres entiers, arrondir, plutôt que de supprimer les décimales. (Sauf pour déduire des inégalités dans le cas)

1) Les éléments de données doivent exister sur les nœuds feuilles

2) Les nœuds non-feuille stockent M-1 mots-clés pour indiquer la direction de recherche i représente le i + 1ème nœud non-feuille ; Le plus petit mot-clé d'un sous-arbre ; en supposant un arbre B+ d'ordre 5, alors il a 5 - 1 = 4 mots-clés.

3) L'arbre B+ n'a qu'un seul nœud feuille comme nœud racine (sans aucun nœud enfant) ; s'il a des nœuds enfants, son numéro de nœud doit appartenir à l'ensemble : 

4) Sauf pour la racine, tous non- Le nombre de nœuds enfants d'un nœud feuille doit appartenir à l'ensemble : { M/2, M} ;

5) Toutes les feuilles sont à la même profondeur, et le nombre d'éléments de données de la feuille les nœuds doivent appartenir à l'ensemble : { L/2, L} ;

2. Cas sélectionnés de M et L

En supposant que la longueur totale de tous les champs ne dépasse pas 500 octets, en prenant une clé primaire de 50 octets comme clé Par exemple, simulez et dérivez l'arbre B+, y compris l'espace occupé par l'enregistrement de ligne lui-même

On sait que tous les enregistrements de ligne consommeront quelques octets pour enregistrer les informations de ligne : telles que les champs de longueur variable, les en-têtes d'enregistrement de ligne, les ID de transaction, les pointeurs d'annulation, etc.

create table context(
	id  varchar(50) primary key,
	name varchar(50) not null,
	description varchar(360)  
);

Un nœud feuille représente une page de données, et la sélection des valeurs M et L y est étroitement liée. Supposons que la taille de la page de données est de : P/octet (en prenant le MySQL discuté dans. cet article à titre d'exemple, une donnée La taille de la page est de 16 Ko, soit 16384 octets)

Sur les nœuds non feuilles : la clé de l'arbre B+ est la clé primaire Dans cet exemple, c'est la clé primaire. supposons que la clé primaire fait 50 octets, et la clé de l'arbre B+ d'ordre M. Elle est M -1, occupant : 50 * (M - 1) octets d'espace

plus sa branche ; pointeur pointant vers M nœuds enfants, en supposant que chaque pointeur de branche occupe 4 mots Stockage de section ; alors dans un nœud non-feuille, la consommation totale d'espace est : 50 * (M - 1) + 4 * M = 54M - 50 octets.

Lorsque vous utilisez MySQL, et en supposant que la clé primaire est de 50 octets, l'inégalité est établie : 54M - 50

Sur le nœud feuille, la capacité maximale de chaque ligne définie dans la table connue est : 500 octets, puis l'expression suivante est établie : L * 500

Comme indiqué ci-dessous, il y a actuellement 5 000 W de données et la hauteur de l'arbre est supérieure à 3, ce qui signifie que nous n'avons besoin que de 4 E/S de disque maximum pour trouver les données.

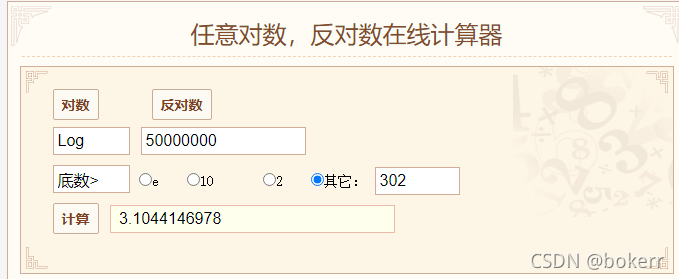
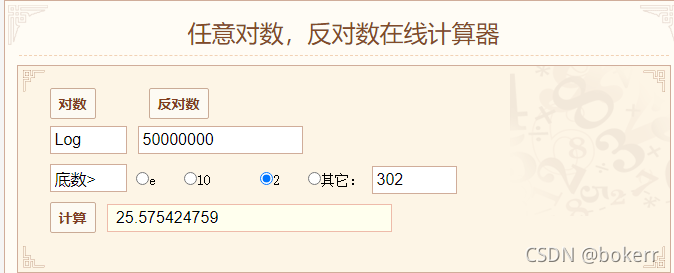
Reportez-vous à la figure ci-dessous, la pire limite temporelle d'un arbre binaire équilibré est : 1,44 * logN = 25,58 * 1,44 = 36,83 ; disons, si les données de 5 000 W sont équilibrées, l'arborescence binaire dépassera 36 E/S disque dans le pire des cas et 26 E/S disque au moins.

L'image montre un arbre B+ ordinaire d'ordre 5 (M = 5), où chaque nœud a un maximum de 5 valeurs​​( L = 5) ; M et L ne sont pas nécessairement égaux, comme dans l’analyse ci-dessus : M et L dépendent de la situation réelle.

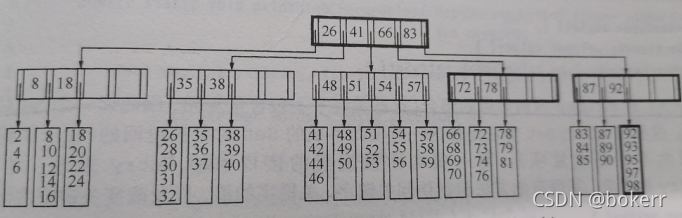
Hahaha, dessiner des images est trop compliqué, j'ai analysé les photos de ce livre à partir de structures de données et d'algorithmes, et je suis aussi intelligent que moi.

Ici, nous parlons uniquement de la définition de l'arbre B+ et des détails de la sélection des paramètres. L'insertion de l'arbre B+ et la suppression de l'arbre B+ ne sont pas abordées en détail.

4. Index de l'arbre B+

Généralement, la hauteur de l'arbre B+ est de 2 à 4 couches, c'est-à-dire que lors de la recherche d'un enregistrement de ligne, cela ne prend généralement que 2~ 4 fois d'E/S disque pour le trouver. La page où se trouve l'enregistrement de ligne. Que l'index clusterisé ou l'index non clusterisé soit hautement équilibré en interne, les données d'indexation sont stockées dans les nœuds feuilles. La différence est que les nœuds feuilles de l'index clusterisé stockent l'intégralité des données d'enregistrement de ligne.

1. Index clusterisé

Les nœuds feuilles de l'index cluster stockent la ligne entière de données, et chaque table ne peut avoir qu'un seul index cluster.

2. Index auxiliaire

Le nœud feuille de l'index auxiliaire stocke la valeur de la clé et un signet. Le signet indique au moteur de stockage Innodb où trouver l'enregistrement de ligne complet correspondant. aux données d’index.

Chaque table peut avoir plusieurs index auxiliaires

Un inconvénient d'index auxiliaires Il est nécessaire d'obtenir les données complètes des lignes via l'index cluster discret, même si le signet stocké dans l'index secondaire a été trouvé.

5. À propos de la valeur de cardinalité

La discussion sur la cardinalité est basée sur un index non clusterisé, et chaque index non clusterisé aura une valeur de cardinalité.

1. Définition de la cardinalité

Il est à noter que toutes les colonnes des conditions de requête n'ont pas besoin d'être indexées, par exemple : le sexe, l'âge, les sujets, etc. petite plage de valeurs et dictionnaire densément distribué, aucune indexation n’est requise.
La cardinalité représente le nombre estimé d'enregistrements uniques dans l'index. Généralement : la cardinalité/le nombre de lignes d'enregistrement dans la table doit être aussi proche que possible de 1 s'il est très petit, vous devez vous demander si l'index doit le faire ; être retiré. (Cette valeur doit être proche de 1 dans un index clusterisé et il n'y a pas de valeur de discussion).

2. Mise à jour de Cardinality

• Dans MySQL, étant donné que chaque moteur de stockage implémente les index d'arborescence B+ différemment, les statistiques de Cardinality sont implémentées au niveau de la couche du moteur de stockage. .

• Lorsque la quantité de données dans le tableau est très importante, il faut beaucoup de temps pour effectuer des statistiques sur la cardinalité, et ses statistiques sont généralement effectuées en utilisant la méthode d'échantillonnage .

• L'existence de la Cardinalité peut nous aider à analyser si l'indice a une signification.

6. Utilisation de l'index arborescent B+

[ Les index abordés dans cette section font principalement référence à des index auxiliaires, et les requêtes sur les index clusterisés sont généralement appelé analyse complète de la table. 】

1. Index conjoint

Un index conjoint est un index construit sur plusieurs colonnes de la table. C'est aussi une structure arborescente B+. c'est qu'il existe plusieurs colonnes.

create table t (
	a int,
	b int,
	primary key (a),
	key idx_ab (a, b)
)engine=innodb;

Dans le tableau ci-dessus, définissez la clé primaire commune idx_ab, et sa structure de stockage est la suivante :

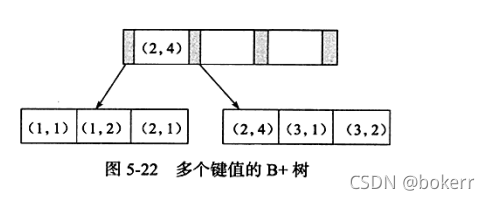
如上图所述，键值有序，需要注意的是，如下SQL可以使用该索引：

	select * from t where a = ? and b = ?
	
	select * from t where a = ?

如下sql 不能使用该索引；查看示例图中联合索引叶子节点存放的数据我们可以发现：两个叶子节点上，关于字段b的存放显然不是有序的。

	select * from t where b = ?

联合索引本身还有一个好处，辅助索引本身已经对第二个键值进行了排序，如下语句可以避免多一次的排序。

	select b from t where a = ?  order by b desc

辅助索引中已经对 b 列进行了排序，所以此时使用辅助索引更高效。

2、覆盖索引

Innodb 支持覆盖索引(covering index，或称为索引覆盖)，即从辅助索引中就可以得到结果，而不需要查询聚集索引中的记录。由于辅助索引不包含完整的行记录，从而比聚集索引小很多，可以极大地减少IO操作。

再形如：select count(*) from table name where b = ? 的sql，如果有满足条件的辅助索引，它会优先使用辅助索引因为辅助索引体积远远小于聚集索引。

3、优化器选择不使用索引的情况

某些情况下，通过EXPLAIN指令会发现一些SQL，并没有选择使用满足条件的辅助索引去查数据，而是直接选择了全表扫描(聚集索引)，这种情况一般发生于 范围查找、join链接操作等情况下。

当发生此类查找时，一般是查找一个较大范围内的数据，当范围较大时同样意味着大量的数据需要再进行一次书签访问去获取完整数据，已知顺序读取速度大于离散读取速度，所以此时不会使用辅助索引，而是直接查聚集索引(整表扫描)。一般情况下，当访问数据超过表中数据总数的20%时，索引覆盖不再适用，而需要进行全表扫描。）

	create table t (
		a int,
		b int,
		primary key (a,b),
		key idx_a (a)
	)engine=innodb;

如上定义表，a和b两列构成联合索引，列a上有独立的辅助索引，对于语句：

select * from  t where  a >= 3  and a<= 1000000;

按理说，该语句是可以选择使用辅助索引 idx_a 进行查找的，但是通过执行 explain 发现该语句发生了全表扫描(聚集索引)，而不是使用辅助索引： idx_a。

4、索引提示

索引提示指MySQL支持在SQL中显式的告诉优化器使用哪个索引。

当优化器选择索引错误，可以手动指定索引。[极小概率事件]

当索引太多时，优化器选择索引的操作时间开销大，此时可以手动指定索引。

使用索引提示的前提是我们自己要对sql的执行非常了解，非常明确该操作能带来更好的效率。

5、Multi-Range Read 优化 (MRR)

MySQL5.6版本开始支持Multi-Range Read (MRR) 优化，它的目的是减少磁盘的离散读，将离散的访问优化为相对有序的访问，它使用于 range ref eq_ref 类型的查询。

1).MRR优化有如下好处：

• 它使得数据访问变得较为顺序，当根据辅助索引查询时，会将查询结果按照主键排序后，再去聚集索引进行书签查询。

• 减少缓冲池中页被替换的次数；

• 批量处理对键值的查询操作；

2).对于 JOIN 和 范围查询，Innodb 中MRR的工作方式为：

• 将通过辅助索引查询到的数据放到一个缓存中，此时这些数据是按照辅助索引键值排序的；

• 将缓存中的数据按照主键顺序排序；

• 根据主键顺序访问实际数据文件；

想象一下，在缓冲池不够大的情况下进行大范围数据查询，会导致数据页频繁被从LRU列表中移除。如果被查询的辅助索引不是按主键排序的，可能会多次发生如下的情况：一个页在同一次查询中被剔出LRU列表后又再次被加载出来。

配置项：read_rnd_buffer_size 用来配置上述描述的键值缓冲区大小，默认为256K；当发生溢出时，执行器只对已经缓存的数据进行排序。

3).对于范围查询：MMR还支持对键值的拆分，将范围查询拆分为键值对进行批量的数据查询.

create table t (
	a integer,
	b integer,
	primary key (a),
	key idx_ab (a, b)
)engine=innodb;

select * from t where a = 50  and  b>= 100 and  b<= 20000

由于存在辅助索引 idx_ab，上述sql语句的条件可以拆分为键值对集合：{( 50 , 100 ),( 50 , 101 ),......,( 50 , 20000 )}，这样就将范围查询优化为对键值对的查询；否则会进行范围查询，将 b ∈ {100，20000} 的所有数据都取出。

Multi-Range Read 是否启用，由如下参数中的，mrr 和 mrr_cost_based 标记进行控制，mrr标记是 MRR优化的开关。若前者设置为on，后者设置为off表示当满足条件时总是使用MRR优化；若前者设置为 on，后者也设置 on 表示通过 cost base 方式判断是否需要 MRR优化。

6. Index Condition Pushdown Optimization (ICP)

L'optimisation ICP est également prise en charge à partir de MySQL 5.6. Il s'agit d'une méthode d'optimisation pour les requêtes basées sur l'index. Elle prend en charge les requêtes de type : range, ref, eq_ref, ref_or_null. Optimiser.

• Lorsque ICP est désactivé, la couche du moteur de stockage parcourt l'index pour localiser l'enregistrement de ligne complet ; puis le renvoie à la couche de base de données (couche serveur), puis filtre les conditions Where pour ces lignes de données.

• Lorsque ICP est activé, si la condition Where peut utiliser un index, MySQL placera cette partie de l'opération de filtrage dans la couche du moteur de stockage. Le moteur de stockage filtre à travers l'index et supprime toute la ligne de données qui satisfait. la condition Where et la renvoie. L'utilisation d'ICP peut réduire la fréquence à laquelle la couche du moteur de stockage accède aux enregistrements de ligne, tout en réduisant le nombre de fois où la couche de base de données (couche serveur) doit accéder au moteur de stockage.

[La condition préalable à l'utilisation de ce filtre est la suivante : la condition du filtre doit être dans la plage que l'index peut couvrir]

Index Condition Pushdown fonctionne comme suit :

1) Lorsque ICP n'est pas utilisé

(1) Lorsque Lorsque le moteur de stockage lit la ligne suivante, il lit l'enregistrement de ligne concerné à partir du nœud feuille de l'index auxiliaire, puis utilise la référence de clé primaire dans le signet de l'enregistrement pour interroger l'enregistrement de ligne complet et le renvoyer. à la couche base de données (couche serveur).

(2) La couche de base de données effectue un filtrage par condition Where sur les enregistrements de ligne complets. Si les données de ligne répondent à la condition Where, elles seront utilisées, sinon elles seront supprimées.

(3) Effectuez l'étape 1 jusqu'à ce que toutes les données qui remplissent les conditions soient lues.

2) Comment effectuer une analyse d'index lors de l'utilisation d'ICP

(1) Le moteur de stockage lit les données de l'index une par une...

(2) Lorsque le moteur de stockage lit les données de l'index, selon le clé de l'index Utilisez la condition Where pour filtrer. Si l'enregistrement de ligne ne remplit pas la condition, le moteur de stockage traitera la donnée suivante (retour à l'étape précédente). Ce n'est que lorsque les conditions de requête sont remplies que les données complètes seront lues à partir de l'index clusterisé.

(3) Enfin, la couche moteur de stockage renverra tous les enregistrements de ligne complets qui répondent aux conditions de requête à la couche de base de données.

(4) Si la couche de base de données continue à être utilisée, les conditions de requête après celles qui ne sont pas couvertes par l'index seront filtrées.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!