Comprendre et unifier 14 algorithmes d'attribution pour rendre les réseaux de neurones interprétables

Bien que les DNN aient connu un large succès dans diverses applications pratiques, leurs processus sont souvent considérés comme des boîtes noires car il est difficile d'expliquer comment les DNN prennent des décisions. Le manque d’interprétabilité compromet la fiabilité des DNN, entravant ainsi leur application généralisée dans des tâches à enjeux élevés telles que la conduite autonome et la médecine IA. Par conséquent, les DNN explicables ont attiré une attention croissante.

En tant que perspective typique pour expliquer le DNN, la méthode d'attribution vise à calculer le score d'attribution/importance/contribution de chaque variable d'entrée à la sortie du réseau. Par exemple, étant donné un DNN pré-entraîné pour la classification d'images et une image d'entrée, le score d'attribut pour chaque variable d'entrée fait référence à l'impact numérique de chaque pixel sur le score de confiance de classification.

Bien que les chercheurs aient proposé de nombreuses méthodes d'attribution ces dernières années, la plupart d'entre elles reposent sur des heuristiques différentes. Il manque actuellement une perspective théorique unifiée pour tester l’exactitude de ces méthodes d’attribution, ou du moins pour élucider mathématiquement leurs mécanismes fondamentaux. Les chercheurs ont tenté d’unifier différentes méthodes d’attribution, mais ces études n’ont couvert que quelques méthodes.

Dans cet article, nous proposons une "explication unifiée du mécanisme intrinsèque de 14 algorithmes d'attribution d'importance des unités d'entrée".

Adresse papier : https://arxiv.org /pdf/2303.01506.pdf

En fait, qu'il s'agisse de « 12 algorithmes pour améliorer la résistance à la migration » ou de « 14 types d'attribution d'importance aux unités d'entrée Les « algorithmes » sont les domaines les plus touchés des algorithmes d’ingénierie. Dans ces deux domaines, la plupart des algorithmes sont empiriques. Les gens conçoivent des algorithmes d’ingénierie plausibles basés sur une expérience expérimentale ou une compréhension intuitive. La plupart des études n'ont pas fait de définitions rigoureuses ni de démonstrations théoriques de « quelle est exactement l'importance des unités d'entrée ». Quelques études ont certaines démonstrations, mais elles sont souvent très imparfaites. Bien entendu, le problème du « manque de définitions et de démonstrations rigoureuses » imprègne tout le domaine de l’intelligence artificielle, mais il est particulièrement prégnant dans ces deux directions.

Premièrement, dans un environnement où de nombreux algorithmes d'attribution empiriques inondent le domaine de l'apprentissage automatique interprétable, nous espérons prouver que « les 14 algorithmes d'attribution (Algorithmes qui expliquent l'importance des unités d'entrée des réseaux neuronaux) peut être exprimée comme une distribution de l'utilité d'interaction modélisée par les réseaux de neurones, et différents algorithmes d'attribution correspondent à différentes proportions de distribution d'utilité d'interaction. De cette façon, bien que différents algorithmes aient des objectifs de conception complètement différents (par exemple, certains algorithmes ont une fonction objectif définie et certains algorithmes sont de purs pipelines), nous avons constaté que mathématiquement, ces algorithmes peuvent être inclus dans la distribution « utilitaire d'interaction » " de logique narrative.

• Sur la base du cadre d'allocation des utilitaires d'interaction ci-dessus, nous pouvons en outre proposer trois critères d'évaluation pour l'algorithme d'attribution de l'importance des unités d'entrée du réseau neuronal afin de mesurer les prédictions de l'algorithme d'attribution. Si la valeur d’importance de l’unité d’entrée est raisonnable.
• Bien sûr, notre analyse théorique n'est pas seulement applicable à 14 algorithmes d'attribution, et peut théoriquement unifier davantage de recherches similaires. En raison d’une main-d’œuvre limitée, nous ne discutons que de 14 algorithmes dans cet article.

La vraie difficulté de la recherche est que différents algorithmes d'attribution empiriques sont souvent construits sur des intuitions différentes, et chaque article s'efforce uniquement d'apprendre de ses propres perspectives "se justifier", et les algorithmes d’attribution sont conçus sur la base de différentes intuitions ou perspectives, mais il manque un langage mathématique standardisé pour décrire uniformément l’essence des différents algorithmes.

Révision de l'algorithme

Avant de parler de mathématiques, cet article passera brièvement en revue l'algorithme précédent d'un niveau intuitif.

1. Algorithme d'attribution basé sur le dégradé. Ce type d'algorithme estime généralement que le gradient de la sortie du réseau neuronal vers chaque unité d'entrée peut refléter l'importance de l'unité d'entrée. Par exemple, l'algorithme Gradient*Input modélise l'importance d'une unité d'entrée en tant que produit élément par élément du gradient et de la valeur de l'unité d'entrée. Considérant que le gradient ne peut refléter que l'importance locale de l'unité d'entrée, les algorithmes Smooth Gradients et Integrated Gradients modélisent l'importance comme le produit élément par élément du gradient moyen et de la valeur de l'unité d'entrée, où le gradient moyen dans ces deux méthodes fait référence. au voisin de l'échantillon d'entrée respectivement. La valeur moyenne du gradient dans le domaine ou le gradient moyen du point d'interpolation linéaire entre l'échantillon d'entrée et le point de référence. De même, l'algorithme Grad-CAM prend la moyenne de la sortie du réseau sur tous les gradients de caractéristiques de chaque canal pour calculer le score d'importance. De plus, l'algorithme des gradients attendus estime que la sélection d'un seul point de référence conduira souvent à des résultats d'attribution biaisés, proposant ainsi de modéliser l'importance comme l'attente des résultats d'attribution des gradients intégrés sous différents points de référence.

2. Algorithme d'attribution basé sur la rétropropagation couche par couche. Les réseaux de neurones profonds sont souvent extrêmement complexes et la structure de chaque couche de réseau neuronal est relativement simple (par exemple, les caractéristiques profondes sont généralement la somme linéaire de caractéristiques superficielles + une fonction d'activation non linéaire), ce qui facilite l'analyse de l'importance de des traits peu profonds aux traits profonds. Par conséquent, ce type d'algorithme obtient l'importance de l'unité d'entrée en estimant l'importance des caractéristiques de niveau intermédiaire et en propageant cette importance couche par couche jusqu'à la couche d'entrée. Les algorithmes de cette catégorie incluent LRP-epsilon, LRP-alphabeta, Deep Taylor, DeepLIFT Rescale, DeepLIFT RevealCancel, DeepShap, etc. La différence fondamentale entre les différents algorithmes de rétropropagation est qu'ils utilisent des règles de propagation d'importance différente couche par couche.

3. Algorithme d'attribution basé sur l'occlusion. Ce type d'algorithme déduit l'importance d'une unité d'entrée en fonction de l'impact de l'occlusion d'une unité d'entrée sur la sortie du modèle. Par exemple, l'algorithme Occlusion-1 (Occlusion-patch) modélise l'importance du i-ème pixel (bloc de pixels) en tant que changement de sortie lorsque le pixel i n'est pas masqué et masqué lorsque les autres pixels ne sont pas masqués. L'algorithme de valeur de Shapley considère de manière exhaustive toutes les situations d'occlusion possibles d'autres pixels et modélise l'importance en tant que moyenne des changements de sortie correspondant au pixel i dans différentes situations d'occlusion. La recherche a prouvé que la valeur de Shapley est le seul algorithme d'attribution qui satisfait aux axiomes de linéarité, de factice, de symétrie et d'efficacité.

Unifier le mécanisme interne de 14 algorithmes d'attribution empiriques

Après une étude approfondie de plusieurs algorithmes d'attribution empiriques, nous ne pouvons nous empêcher de réfléchir à une question : au niveau mathématique, quel est le problème de l'attribution des réseaux de neurones résoudre ? Existe-t-il une modélisation mathématique et un paradigme unifiés derrière de nombreux algorithmes d'attribution empiriques ? À cette fin, nous essayons d’examiner les questions ci-dessus en partant de la définition de l’attribution. L'attribution fait référence au score d'importance/contribution de chaque unité d'entrée à la sortie du réseau neuronal. Ensuite, la clé pour résoudre le problème ci-dessus est de (1) modéliser le « mécanisme d'influence de l'unité d'entrée sur la sortie du réseau » au niveau mathématique, et (2) d'expliquer combien d'algorithmes d'attribution empiriques utilisent ce mécanisme d'influence pour concevoir l'importance Formule d'attribution.

Concernant le premier point clé, nos recherches ont révélé que chaque unité d'entrée affecte souvent la sortie du réseau neuronal de deux manières. D'une part, une certaine unité d'entrée n'a pas besoin de s'appuyer sur d'autres unités d'entrée et peut agir indépendamment et affecter la sortie du réseau. Ce type d'influence est appelé « effet indépendant ». D'un autre côté, une unité d'entrée doit coopérer avec d'autres unités d'entrée pour former un certain modèle, affectant ainsi la sortie du réseau. Ce type d'influence est appelé « effet d'interaction ». Notre théorie prouve que la sortie du réseau neuronal peut être rigoureusement déconstruite en effets indépendants de différentes variables d'entrée, ainsi qu'en effets interactifs entre les variables d'entrée dans différents ensembles.

Parmi eux, représente l'effet indépendant de la i-ème unité d'entrée, #🎜🎜 ##🎜 🎜# représente l'effet d'interaction entre plusieurs unités d'entrée dans l'ensemble S. Concernant le deuxième point clé, nous avons exploré et constaté que les mécanismes internes des 14 algorithmes d'attribution empiriques existants peuvent représenter une allocation de l'utilité indépendante et de l'utilité interactive ci-dessus, mais que différents algorithmes d'attribution allouent des utilités indépendantes et interactives. utilité aux unités d'entrée du réseau neuronal dans différentes proportions. Plus précisément, laissez ​ # 🎜 🎜#​ représente le score d'attribution de la i-ème unité d'entrée. Nous prouvons rigoureusement que le obtenu par les 14 algorithmes d'attribution empiriques peut être uniformément exprimé comme le paradigme mathématique suivant (c'est-à-dire la somme pondérée de l'utilité indépendante et de l'utilité interactive) : #🎜 🎜 ## 🎜🎜 # # 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜🎜 # # 🎜🎜 ## 🎜🎜 ## 🎜🎜 ## 🎜 🎜 🎜 # ​Parmi eux, reflète proportion de l'effet indépendant de la j-ème unité d'entrée allouée à la i-ème unité d'entrée, représente l'allocation des effets interactifs entre plusieurs unités d'entrée dans l'ensemble S à la i-ème proportions de l'unité d'entrée. La « différence fondamentale » entre de nombreux algorithmes d'attribution est que différents algorithmes d'attribution correspondent à différents ratios d'attribution .

Le tableau 1 montre comment quatorze algorithmes d'attribution différents attribuent respectivement des effets indépendants et des effets interactifs.

Graphique 1. Quatorze types Attribution les algorithmes peuvent être écrits comme un paradigme mathématique de la somme pondérée des effets indépendants et des effets interactifs. Parmi eux,

représente respectivement l'effet indépendant de Taylor et l'effet d'interaction de Taylor, satisfaisant

est un raffinement de l'effet indépendant 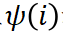et de l'effet interactif .

min Trois principes majeurs

Dans la recherche sur les explications d'attribution, en raison de Il n'y a aucun moyen d'obtenir/étiqueter la vraie valeur de l'explication d'attribution du réseau neuronal, et les gens ne peuvent pas évaluer la fiabilité d'un certain algorithme d'explication d'attribution d'un point de vue empirique. Le défaut fondamental du « manque de critères objectifs d’évaluation de la fiabilité des algorithmes d’explication d’attribution » a suscité de nombreuses critiques et remises en question dans le domaine universitaire de la recherche sur l’explication d’attribution.

La révélation du mécanisme public des algorithmes d'attribution dans cette étude nous permet d'évaluer et de comparer équitablement la fiabilité de différents algorithmes d'attribution dans le même cadre théorique. Plus précisément, nous proposons les trois critères d'évaluation suivants pour évaluer si un certain algorithme d'attribution distribue les effets indépendants et les effets interactifs de manière équitable et raisonnable.

(1)Critère 1 : Couvrir tous les effets indépendants et effets interactifs dans le processus d'attribution. Après avoir déconstruit la sortie du réseau neuronal en effets indépendants et effets interactifs, un algorithme d'attribution fiable devrait couvrir autant que possible tous les effets indépendants et effets interactifs dans le processus d'allocation. Par exemple, l'attribution à la phrase Je ne suis pas heureux devrait couvrir tous les effets indépendants des trois mots Je ne suis pas heureux, ainsi que J (Je ne suis pas heureux), J (Je suis heureux). ), J (pas, heureux), J (je ne suis pas heureux), etc. tous les effets d'interaction possibles.

(2)Ligne directrice 2 : Évitez d'attribuer des effets et des interactions indépendants à des unités d'entrée non pertinentes. L’effet indépendant de la ième unité d’entrée ne doit être attribué qu’à la ième unité d’entrée et non à d’autres unités d’entrée. De même, l’effet d’interaction entre les unités d’entrée au sein de l’ensemble S ne doit être attribué qu’aux unités d’entrée au sein de l’ensemble S et non aux unités d’entrée en dehors de l’ensemble S (ne participant pas à l’interaction). Par exemple, l’effet d’interaction entre pas et heureux ne doit pas être attribué au mot je suis.

(3)Troisième principe : allocation complète. Chaque effet indépendant (effet d'interaction) doit être entièrement attribué à l'unité d'entrée correspondante. En d'autres termes, les valeurs d'attribution attribuées à toutes les unités d'entrée correspondantes par un certain effet indépendant (effet d'interaction) doivent correspondre exactement à la valeur de l'effet indépendant (effet d'interaction). Par exemple, l'effet d'interaction J (pas, heureux) attribuerait une partie de l'effet (pas, heureux) au mot pas et une partie de l'effet (pas, heureux) au mot heureux. Ensuite, le ratio de répartition devrait satisfaire .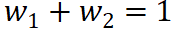

Ensuite, nous avons utilisé ces trois critères d'évaluation pour évaluer les 14 algorithmes d'attribution différents ci-dessus (comme indiqué dans le tableau 2). Nous avons constaté que les algorithmes Integrated Gradients, Expected Gradients, Shapley value, Deep Shap, DeepLIFT Rescale et DeepLIFT RevealCancel satisfont à tous les critères de fiabilité.

Tableau 2. Résumé indiquant si 14 algorithmes d'attribution différents satisfont aux trois critères d'évaluation de la fiabilité.

Présentation de l'auteur

L'auteur de cet article, Deng Huiqi, est titulaire d'un doctorat en mathématiques appliquées de l'Université Sun Yat-sen. Au cours de son doctorat, il a visité l'Université baptiste de Hong Kong et. du Département d'informatique de la Texas A&M University, et mène actuellement des recherches postdoctorales au sein de l'équipe du professeur Zhang Quanshi. L'orientation de la recherche est principalement l'apprentissage automatique fiable/interprétable, notamment en expliquant l'importance de l'attribution des réseaux de neurones profonds, en expliquant la capacité d'expression des réseaux de neurones, etc.

Deng Huiqi a fait beaucoup de travail au début. Le professeur Zhang l'a simplement aidée à réorganiser la théorie une fois le travail initial terminé pour rendre la méthode et le système de preuve plus fluides. Deng Huiqi n'a pas rédigé beaucoup d'articles avant d'obtenir son diplôme. Après avoir rejoint le professeur Zhang fin 2021, il a effectué trois tâches en plus d'un an dans le cadre du système d'interaction de jeu, notamment (1) découvrir et expliquer théoriquement le goulot d'étranglement de la représentation commune des neurones. Les réseaux, c'est-à-dire que les réseaux de neurones se sont révélés encore moins aptes à modéliser des représentations interactives de complexité modérée. Ce travail a eu la chance d'être sélectionné comme article oral de l'ICLR 2022 et sa note de révision s'est classée parmi les cinq premières (score 8 8 8 10). (2) La théorie prouve la tendance à la représentation conceptuelle des réseaux bayésiens et fournit une nouvelle perspective pour expliquer les performances de classification, la capacité de généralisation et la robustesse contradictoire des réseaux bayésiens. (3) Explique théoriquement la capacité du réseau neuronal à apprendre des concepts interactifs de complexité différente au cours du processus de formation.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!