Maison >Périphériques technologiques >IA >Cet article vous aidera à comprendre ce qu'est la descente de gradient
Cet article vous aidera à comprendre ce qu'est la descente de gradient
- 王林avant
- 2023-05-17 17:04:122870parcourir

La descente de gradient est la source d'énergie de l'apprentissage automatique
Après les deux sections précédentes, nous pouvons commencer à parler de la source d'énergie de l'apprentissage automatique : la descente de gradient.
La descente de gradient n'est pas un outil mathématique très compliqué. Son histoire remonte à plus de 200 ans. Cependant, les gens ne s'attendaient peut-être pas à ce qu'un outil mathématique aussi simple devienne la base de nombreux algorithmes d'apprentissage automatique, et il coopérera également. avec les réseaux de neurones a déclenché la révolution de l’apprentissage profond.
1. Qu'est-ce que le gradient
Trouvez les dérivées partielles de chaque paramètre d'une fonction multivariée, puis écrivez les dérivées partielles obtenues de chaque paramètre sous la forme d'un vecteur, qui est le gradient.
Plus précisément, la fonction f (x1, x2) des deux variables indépendantes correspond aux deux caractéristiques de l'ensemble de données d'apprentissage automatique. Si les dérivées partielles sont obtenues pour x1 et x2 respectivement, alors le vecteur gradient obtenu est (∂f). /∂x1, ∂f/∂x2) T, qui peut être exprimé mathématiquement par Δf (x1, x2). Alors à quoi ça sert de calculer le vecteur gradient ? Sa signification géométrique est la direction dans laquelle la fonction change, et c'est la direction qui change le plus rapidement. Pour la fonction f(x), au point (x0, y0), la direction du vecteur gradient est la direction dans laquelle la valeur y augmente le plus rapidement. En d’autres termes, dans la direction du vecteur gradient Δf (x0), la valeur maximale de la fonction peut être trouvée. D'autre part, dans la direction opposée du vecteur gradient, c'est-à-dire la direction de -Δf (x0), le gradient diminue le plus rapidement et la valeur minimale de la fonction peut être trouvée. Si la valeur du vecteur gradient en un certain point est 0, alors il a atteint le point le plus bas (ou le point le plus bas local) de la fonction avec une dérivée de 0.
2. Descente de gradient : métaphore de la descente
Il est très courant d'utiliser la descente comme métaphore de la descente de gradient dans l'apprentissage automatique. Imaginez que vous vous tenez quelque part sur une grande montagne, regardant le terrain sans fin au loin, sachant seulement que l'emplacement au loin est beaucoup plus bas qu'ici. Vous voulez savoir comment descendre la montagne, mais vous ne pouvez descendre que étape par étape, c'est-à-dire qu'à chaque fois que vous atteignez une position, trouvez la pente de la position actuelle. Ensuite, faites un pas vers le bas dans la direction négative de la pente, c'est-à-dire descendez l'endroit le plus raide, continuez à résoudre la pente de la nouvelle position et continuez à descendre le long de l'endroit le plus raide à la nouvelle position. Marchez pas à pas jusqu’à atteindre le pied de la montagne, comme le montre l’image ci-dessous.
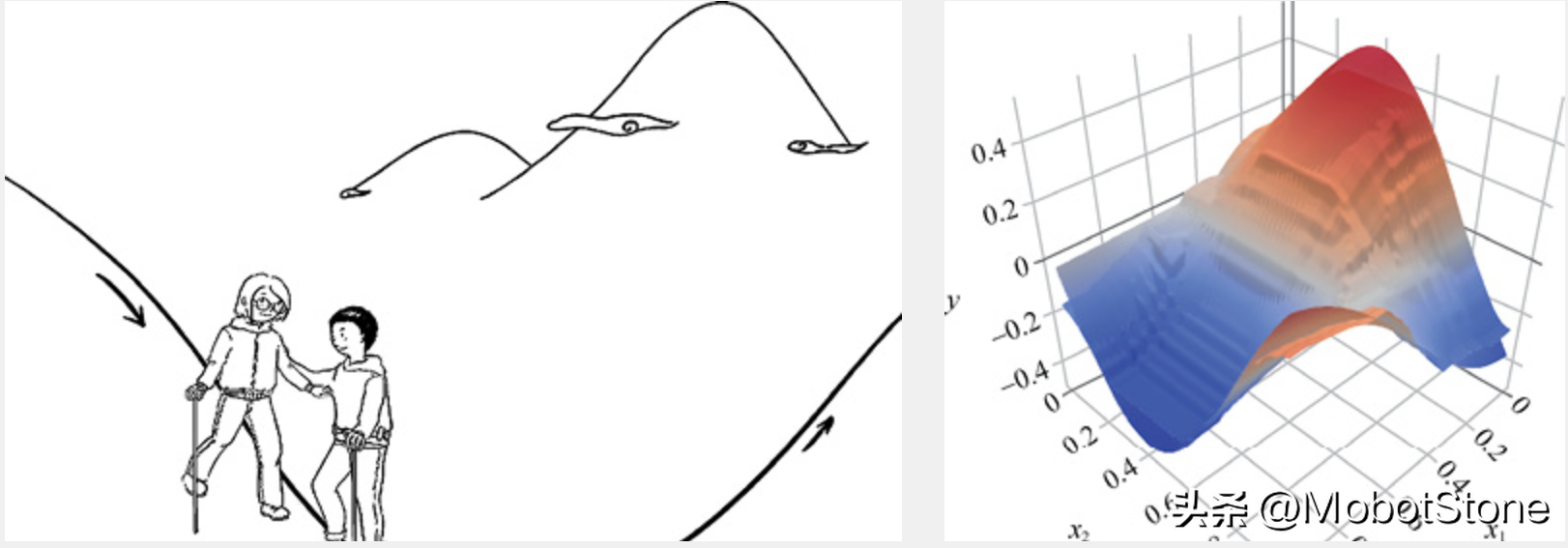
D'après l'explication ci-dessus, il n'est pas difficile de comprendre pourquoi nous venons de mentionner la concavité et la convexité de la fonction. Parce que, dans une fonction non convexe, il peut ne pas atteindre le bas de la montagne, mais s'arrêter à une certaine vallée. En d’autres termes, la descente de gradient pour les fonctions non convexes ne trouve pas toujours la solution optimale globale et ne peut obtenir qu’une solution optimale locale. Cependant, si la fonction est convexe, alors la méthode de descente de gradient peut théoriquement obtenir la solution optimale globale.
3. À quoi sert la descente de gradient ?
La descente de gradient est très utile dans l'apprentissage automatique. En termes simples, vous pouvez prêter attention aux points suivants.
L'essence de l'apprentissage automatique est de trouver la fonction optimale.
Comment mesurer si une fonction est optimale ? La méthode consiste à minimiser l’erreur entre la valeur prédite et la valeur réelle (également appelée valeur de perte en apprentissage automatique).
Vous pouvez établir une fonction entre l'erreur et les paramètres du modèle (de préférence une fonction convexe).
La descente de gradient peut nous guider vers le minimum global de la fonction convexe, c'est-à-dire trouver les paramètres avec la plus petite erreur.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

