Définition du meilleur seuil pour les modèles d'apprentissage automatique : 0,5 est-il le meilleur seuil pour la classification binaire ?

Pour la classification binaire, le classificateur génère un score à valeur réelle, puis seuille la valeur pour produire une réponse binaire. Par exemple, la régression logistique génère une probabilité (une valeur comprise entre 0,0 et 1,0) ; les observations avec des scores égaux ou supérieurs à 0,5 produisent une sortie positive (de nombreux autres modèles utilisent un seuil de 0,5 par défaut).

Mais utiliser le seuil par défaut de 0,5 n'est pas idéal. Dans cet article, je vais montrer comment choisir le meilleur seuil parmi un classificateur binaire. Cet article utilisera Plomber pour exécuter nos expériences en parallèle et utilisera sklearn-evaluation pour générer des graphiques.

Voici un exemple de régression logistique de formation. Supposons que nous développions un système de modération de contenu, dans lequel le modèle signale les publications contenant du contenu préjudiciable (images, vidéos, etc.) ; un humain les examine ensuite et décide si le contenu doit être supprimé.

Créez un classificateur binaire simple

L'extrait de code suivant entraîne notre classificateur :

import matplotlib.pyplot as plt
 import matplotlib as mpl
 from sklearn import datasets
 from sklearn.linear_model import LogisticRegression
 from sklearn.model_selection import train_test_split
 from sklearn_evaluation.plot import ConfusionMatrix
 
 # matplotlib settings
 mpl.rcParams['figure.figsize'] = (4, 4)
 mpl.rcParams['figure.dpi'] = 150
 
 # create sample dataset
 X, y = datasets.make_classification(1000, 10, n_informative=5, class_sep=0.4)
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
 
 # fit model
 clf = LogisticRegression()
 _ = clf.fit(X_train, y_train)

Maintenant, faisons des prédictions sur l'ensemble de test et évaluons les performances à travers la matrice de confusion :

# predict on the test set
 y_pred = clf.predict(X_test)
 
 # plot confusion matrix
 cm_dot_five = ConfusionMatrix(y_test, y_pred)
 cm_dot_five

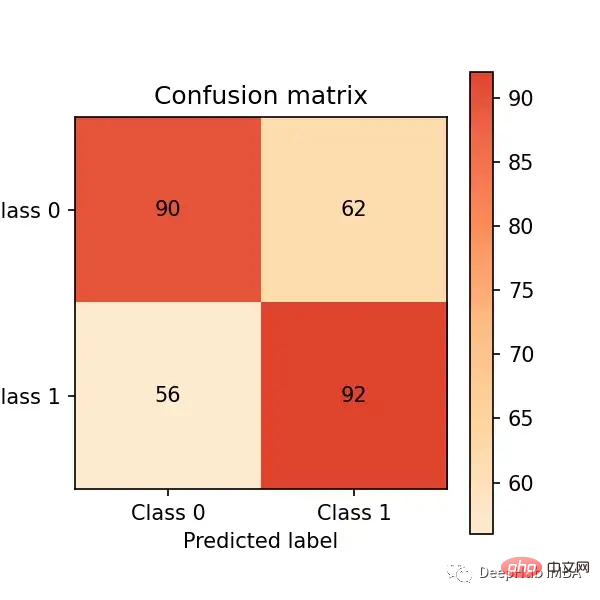
La matrice de confusion résume les performances du modèle dans quatre régions :

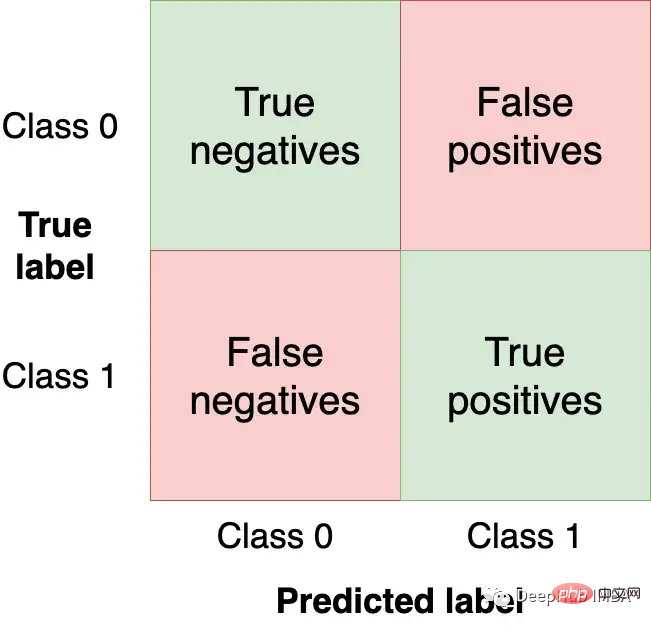
Nous voulons obtenir autant d'observations (à partir de l'ensemble de test) que possible dans les quadrants supérieur gauche et inférieur droit car ce sont les observations correctes que notre modèle doit obtenir. Les autres quadrants sont des erreurs de modèle.

Changer le seuil du modèle modifiera les valeurs dans la matrice de confusion. Dans l'exemple précédent, en utilisant clf.predict, une réponse binaire a été renvoyée (c'est-à-dire en utilisant 0,5 comme seuil) mais nous pouvons utiliser la fonction clf.predict_proba pour obtenir la probabilité brute et utiliser un seuil personnalisé :

y_score = clf.predict_proba(X_test)

Nous pouvons le faire ceci en définissant un seuil A bas plus grand (c'est-à-dire signaler plus de publications comme nuisibles) pour rendre notre classificateur plus agressif et créer une nouvelle matrice de confusion :

cm_dot_four = ConfusionMatrix(y_score[:, 1] >= 0.4, y_pred)

La bibliothèque sklearn-evaluation facilite la comparaison des deux matrices :

cm_dot_five + cm_dot_four

Le le haut du triangle vient d'un seuil de 0,5, le bas vient d'un seuil de 0,4 :

• Les deux modèles prédisent 0 pour le même nombre d'observations (c'est une coïncidence). Seuil de 0,5 : (90 + 56 = 146). Seuil de 0,4 : (78 + 68 = 146)
• Abaisser le seuil entraînera plus de faux négatifs (de 56 à 68)
• Abaisser le seuil augmentera considérablement les vrais positifs (de 92 à 154)

Petits changements de seuil affectent grandement la matrice de confusion. Nous n'avons analysé que deux seuils. Ensuite, si nous pouvons analyser les performances du modèle pour toutes les valeurs, nous pouvons mieux comprendre la dynamique des seuils. Mais avant que cela puisse se produire, de nouvelles mesures d’évaluation des modèles doivent être définies.

Jusqu'à présent, nous avons utilisé des nombres absolus pour évaluer nos modèles. Pour faciliter la comparaison et l'évaluation, nous allons maintenant définir deux métriques normalisées (leurs valeurs sont comprises entre 0,0 et 1,0).

La précision est la proportion d'événements observés qui sont étiquetés (par exemple, les publications que notre modèle juge nuisibles, elles le sont). Le rappel est la proportion d'événements réels récupérés par notre modèle (c'est-à-dire, parmi tous les messages nuisibles, quelle proportion d'entre eux nous avons pu détecter).

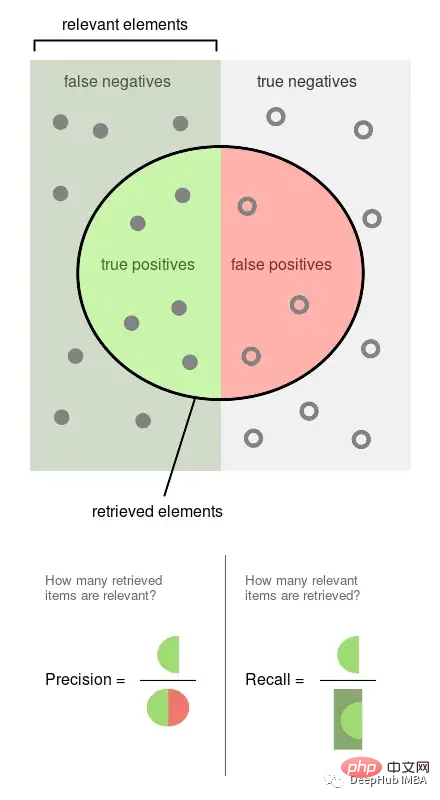
L'image ci-dessus provient de Wikipédia, qui peut bien illustrer la manière dont ces deux indicateurs sont calculés. La précision et le rappel sont tous deux proportionnels, ils sont donc tous deux dans un rapport de 0 à 1.

Lancer l'expérience

Nous obtiendrons de la précision, du rappel et d'autres statistiques basées sur plusieurs seuils pour mieux comprendre comment les seuils les affectent. Nous répéterons également cette expérience plusieurs fois pour mesurer la variabilité.

Les commandes de cette section sont toutes des commandes bash. Ils doivent être exécutés dans le terminal. Si vous utilisez Jupyter, vous pouvez utiliser la commande magique %%sh.

Ici, nous utilisons Plomber Cloud pour exécuter nos expériences. Parce que cela nous permet de mener des expériences en parallèle et de récupérer rapidement les résultats.

Création d'un Notebook qui correspond à un modèle et calcule des statistiques pour plusieurs seuils, en exécutant le même Notebook 20 fois en parallèle.

curl -O https://raw.githubusercontent.com/ploomber/posts/master/threshold/fit.ipynb?utm_source=medium&utm_medium=blog&utm_campaign=threshold

Exécutons ce Notebook (la configuration dans le fichier demandera à Plomber Cloud de l'exécuter 20 fois en parallèle) :

ploomber cloud nb fit.ipynb

Dans quelques minutes nous verrons que les 20 expériences sont terminées :

ploomber cloud status @latest --summary
 
 status count
 -------- -------
 finished 20
 
 Pipeline finished. Check outputs:
 $ ploomber cloud products

Téléchargeons le stockage dans les résultats expérimentaux dans des fichiers .csv :

ploomber cloud download 'threshold-selection/*.csv' --summary

Visualisation des résultats expérimentaux

chargera les résultats de toutes les expériences et les tracera en une seule fois.

 from glob import glob
 
 import pandas as pd
 import numpy as np
 paths = glob('threshold-selection/**/*.csv')
 metrics = [pd.read_csv(path) for path in paths]
 
 for idx, df in enumerate(metrics):
plt.plot(df.threshold, df.precision, color='blue', alpha=0.2,
label='precision' if idx == 0 else None)
plt.plot(df.threshold, df.recall, color='green', alpha=0.2,
label='recall' if idx == 0 else None)
plt.plot(df.threshold, df.f1, color='orange', alpha=0.2,
label='f1' if idx == 0 else None)
 
 
 plt.grid()
 plt.legend()
 plt.xlabel('Threshold')
 plt.ylabel('Metric value')
 
 for handle in plt.legend().legendHandles:
handle.set_alpha(1)
 
 ax = plt.twinx()
 
 for idx, df in enumerate(metrics):
ax.plot(df.threshold, df.n_flagged,
label='flagged' if idx == 0 else None,
color='red', alpha=0.2)
 
 plt.ylabel('Flagged')
 ax.legend(loc=0)
 ax.legend().legendHandles[0].set_alpha(1)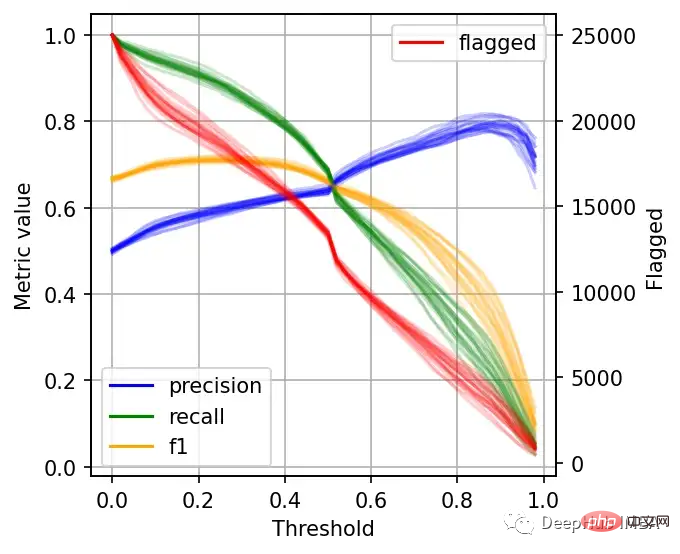

左边的刻度(从0到1)是我们的三个指标:精度、召回率和F1。F1分为精度与查全率的调和平均值，F1分的最佳值为1.0，最差值为0.0;F1对精度和召回率都是相同对待的，所以你可以看到它在两者之间保持平衡。如果你正在处理一个精确度和召回率都很重要的用例，那么最大化F1是一种可以帮助你优化分类器阈值的方法。

这里还包括一条红色曲线(右侧的比例)，显示我们的模型标记为有害内容的案例数量。

在这个的内容审核示例中，可能有X个的工作人员来人工审核模型标记的有害帖子，但是他们人数是有限的，因此考虑标记帖子的总数可以帮助我们更好地选择阈值:例如每天只能检查5000个帖子，那么模型找到10,000帖并不会带来任何的提高。如果我人工每天可以处理10000贴，但是模型只标记了100贴，那么显然也是浪费的。

当设置较低的阈值时，有较高的召回率(我们检索了大部分实际上有害的帖子)，但精度较低(包含了许多无害的帖子)。如果我们提高阈值，情况就会反转:召回率下降(错过了许多有害的帖子)，但精确度很高(大多数标记的帖子都是有害的)。

所以在为我们的二元分类器选择阈值时，我们必须在精度或召回率上妥协，因为没有一个分类器是完美的。我们来讨论一下如何推理选择合适的阈值。

选择最佳阈值

右边的数据会产生噪声(较大的阈值)。需要稍微清理一下，我们将重新创建这个图，我们将绘制2.5%、50%和97.5%的百分位数，而不是绘制所有值。

shape = (df.shape[0], len(metrics))
 precision = np.zeros(shape)
 recall = np.zeros(shape)
 f1 = np.zeros(shape)
 n_flagged = np.zeros(shape)
 for i, df in enumerate(metrics):
precision[:, i] = df.precision.values
recall[:, i] = df.recall.values
f1[:, i] = df.f1.values
n_flagged[:, i] = df.n_flagged.values
 precision_ = np.quantile(precision, q=0.5, axis=1)
 recall_ = np.quantile(recall, q=0.5, axis=1)
 f1_ = np.quantile(f1, q=0.5, axis=1)
 n_flagged_ = np.quantile(n_flagged, q=0.5, axis=1)
 plt.plot(df.threshold, precision_, color='blue', label='precision')
 plt.plot(df.threshold, recall_, color='green', label='recall')
 plt.plot(df.threshold, f1_, color='orange', label='f1')
 
 plt.fill_between(df.threshold, precision_interval[0],
precision_interval[1], color='blue',
alpha=0.2)
 
 plt.fill_between(df.threshold, recall_interval[0],
recall_interval[1], color='green',
alpha=0.2)
 
 
 plt.fill_between(df.threshold, f1_interval[0],
f1_interval[1], color='orange',
alpha=0.2)
 plt.xlabel('Threshold')
 plt.ylabel('Metric value')
 plt.legend()
 
 ax = plt.twinx()
 ax.plot(df.threshold, n_flagged_, color='red', label='flagged')
 ax.fill_between(df.threshold, n_flagged_interval[0],
n_flagged_interval[1], color='red',
alpha=0.2)
 
 ax.legend(loc=3)
 
 plt.ylabel('Flagged')
 plt.grid()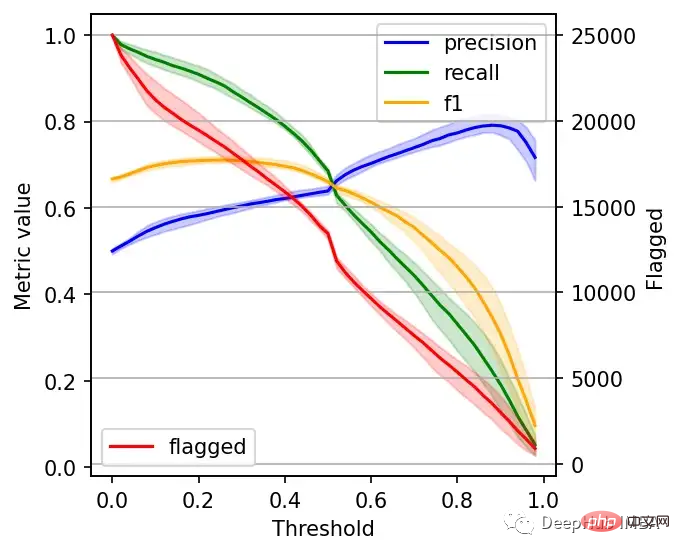

我们可以根据自己的需求选择阈值，例如检索尽可能多的有害帖子(高召回率)是否更重要?还是要有更高的确定性，我们标记的必须是有害的(高精度)?

如果两者都同等重要，那么在这些条件下优化的常用方法就是最大化F-1分数:

idx = np.argmax(f1_)
 prec_lower, prec_upper = precision_interval[0][idx], precision_interval[1][idx]
 rec_lower, rec_upper = recall_interval[0][idx], recall_interval[1][idx]
 threshold = df.threshold[idx]
 
 print(f'Max F1 score: {f1_[idx]:.2f}')
 print('Metrics when maximizing F1 score:')
 print(f' - Threshold: {threshold:.2f}')
 print(f' - Precision range: ({prec_lower:.2f}, {prec_upper:.2f})')
 print(f' - Recall range: ({rec_lower:.2f}, {rec_upper:.2f})')
 
 #结果
 Max F1 score: 0.71
 Metrics when maximizing F1 score:
- Threshold: 0.26
- Precision range: (0.58, 0.61)
- Recall range: (0.86, 0.90)

在很多情况下很难决定这个折中，所以加入一些约束条件会有一些帮助。

假设我们有10个人审查有害的帖子，他们可以一起检查5000个。那么让我们看看指标，如果我们修改了阈值，让它标记了大约5000个帖子:

idx = np.argmax(n_flagged_ <= 5000)
 
 prec_lower, prec_upper = precision_interval[0][idx], precision_interval[1][idx]
 rec_lower, rec_upper = recall_interval[0][idx], recall_interval[1][idx]
 threshold = df.threshold[idx]
 
 print('Metrics when limiting to a maximum of 5,000 flagged events:')
 print(f' - Threshold: {threshold:.2f}')
 print(f' - Precision range: ({prec_lower:.2f}, {prec_upper:.2f})')
 print(f' - Recall range: ({rec_lower:.2f}, {rec_upper:.2f})')
 
 # 结果
 Metrics when limiting to a maximum of 5,000 flagged events:
- Threshold: 0.82
- Precision range: (0.77, 0.81)
- Recall range: (0.25, 0.36)

如果需要进行汇报，我们可以在在展示结果时展示一些替代方案:比如在当前约束条件下(5000个帖子)的模型性能，以及如果我们增加团队(比如通过增加一倍的规模)，我们可以做得更好。

总结

二元分类器的最佳阈值是针对业务结果进行优化并考虑到流程限制的阈值。通过本文中描述的过程，你可以更好地为用例决定最佳阈值。

另外，Ploomber Cloud!提供一些免费的算力!如果你需要一些免费的服务可以试试它。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!