En convertissant des problèmes mathématiques en code, les recherches de Google ont considérablement amélioré la précision des preuves automatiques.

Les ordinateurs sont utilisés depuis un certain temps pour vérifier les preuves mathématiques, mais ils ne peuvent le faire que s'ils préparent des problèmes en utilisant un langage de preuve spécialement conçu et ne peuvent pas gérer le mélange de notation mathématique et de texte écrit utilisé par les mathématiciens.

Si vous convertissez des problèmes mathématiques écrits en langage naturel en codes formels et que vous les rendez plus faciles à résoudre par les ordinateurs, cela peut aider à construire des machines capables d'explorer de nouvelles découvertes en mathématiques.

Ce processus est appelé formalisation, mais une seule preuve peut prendre des années de travail, donc seule une petite partie des connaissances mathématiques est formalisée puis prouvée par des machines.

L'autoformalisation fait référence à la tâche de traduire automatiquement les mathématiques du langage naturel au langage formel. Les implications pratiques et philosophiques d’un outil de formalisation automatisé efficace seraient énormes, il pourrait réduire les coûts de formalisation excessifs actuels et, à long terme, il pourrait relier les aspects automatisés du raisonnement mathématique dans divers domaines de recherche.

Dans une étude récente, Yuhuai Wu de Google et ses collaborateurs ont utilisé les réseaux de neurones d'OpenAI Codex pour automatiser le travail de formalisation. Codex a été formé sur de grandes quantités de texte et de données de programmation provenant du Web, et les programmeurs peuvent l'utiliser pour générer un code fiable.

Lien papier : https://arxiv.org/pdf/2205.12615.pdf

Formalisation de 12 500 problèmes de concours de mathématiques au collège

Une série d'avancées récentes dans les grands modèles de langage démontrent la capacité des modèles à comprendre les langages formels potentiel. Cependant, les succès existants se sont limités aux langages formels (comme Python) pour lesquels de grands corpus existent sur le web. En revanche, les données mathématiques formelles sont très rares. L'une des plus grandes bibliothèques de langage mathématique formel, Archive of Formal Proofs, ne fait que 180 Mo, soit moins de 0,18 % des données de formation du grand modèle de langage Codex.

De plus, contrairement aux langages de programmation à usage général, où les docstrings en langage naturel sont largement disponibles, il y a peu d'alignement des données entre les langages naturels et les langages mathématiques formels. Par conséquent, on ne sait toujours pas si le succès des modèles de langage à grande échelle peut directement promouvoir le développement de la formalisation automatique.

Compte tenu des similitudes entre les langages de preuve et les langages de programmation, l'équipe a décidé de voir si Codex pouvait formaliser une bibliothèque de 12 500 problèmes de concours de mathématiques au collège. Il est capable de convertir un quart des problèmes dans un format compatible avec le solveur de preuves formelles Isabelle.

Wu a déclaré que de nombreuses transformations infructueuses sont le résultat du fait que le système ne comprend pas certains concepts mathématiques. "Si vous montrez le modèle avec un exemple qui explique le concept, alors le modèle peut le comprendre rapidement."

Ce travail explore la perspective d'une formalisation automatique de grands modèles de langage. Les chercheurs ont découvert que les grands modèles de langage sont déjà interactifs. Le prouveur de théorème de formule a une très bonne capacité à formaliser les mathématiques en langage naturel.

La figure 1 ci-dessous est un parfait exemple de formalisation automatique. Non seulement le modèle convertit le code Isabelle syntaxiquement correct, mais il est également capable de capturer des points de raisonnement importants en langage naturel.

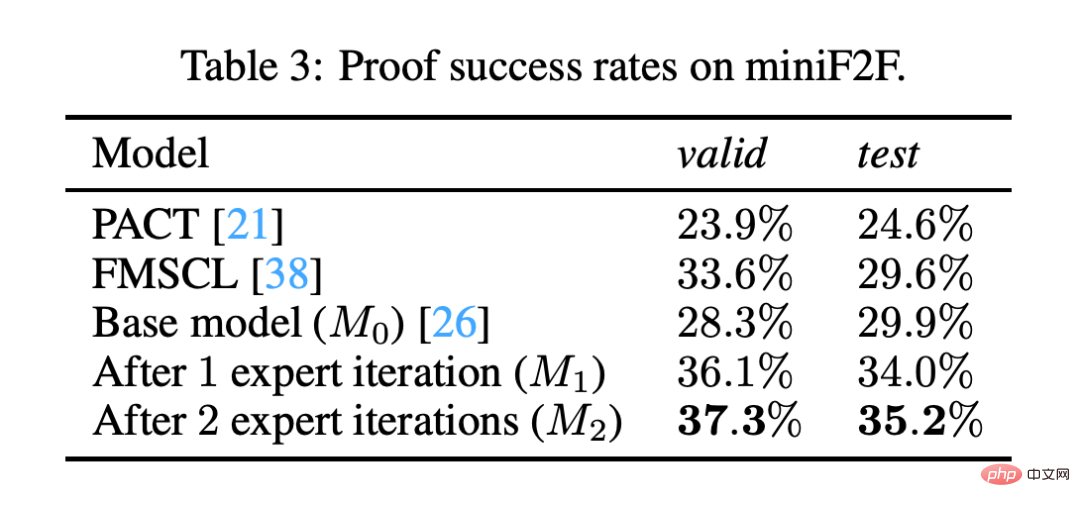
Pour tester l'efficacité de ce formaliseur automatique, l'équipe a ensuite appliqué le Codex à un ensemble de problèmes qui avaient déjà des versions formalisées par l'homme, et le Codex a également généré ses propres versions formalisées de ces problèmes. L’équipe a utilisé une autre IA appelée MiniF2F pour résoudre les deux versions du problème.

La formalisation automatique du problème augmente le taux de réussite de MiniF2F de 29 % à 35 %, ce qui indique que le Codex a fait des progrès importants dans la formalisation du problème.

Il convient de noter que les présentations dans de nombreux concours de mathématiques ont tendance à se présenter sous une forme où il est demandé de trouver la réponse à une certaine question plutôt que de prouver une proposition donnée. Cependant, les énoncés mathématiques formels se présentent sous la forme de propositions et non de questions.

Afin de convertir une question en proposition, le chercheur a joint « La réponse finale » après la question :

Le format d'invite utilisé pour la formalisation automatique est :

L'IA rivalisera-t-elle avec les mathématiciens humains ?

C'est un développement intéressant, mais Wu a déclaré que le travail de l'équipe n'est qu'une preuve de concept. "Si l'objectif est de former une machine comparable aux meilleurs mathématiciens humains, alors la formalisation automatique semble être la voie clé pour atteindre cet objectif."

Albert Jiang, membre de l'équipe de l'Université de Cambridge, a déclaré que si le Le taux de réussite est encore amélioré, l'IA pourra rivaliser avec les mathématiciens humains. "Si nous atteignons 100 %, nous créerons certainement un agent d'IA qui remportera la médaille d'or de l'Olympiade mathématique internationale."

L'objectif immédiat de l'équipe est d'améliorer les modèles formels automatiques et les machines de preuve automatisées, mais l'avenir des résultats de la recherche l’impact sera considérable. Wu affirme que ces modèles peuvent révéler des domaines mathématiques actuellement inconnus des humains.

Les capacités de raisonnement de cette machine sont également très adaptées aux tâches de vérification dans un plus large éventail de domaines. "Vous pouvez vérifier qu'un logiciel fait exactement ce que vous voulez qu'il fasse, ou vous pouvez vérifier une puce matérielle, afin qu'elle ait des applications à la fois dans les algorithmes de trading financier et dans la conception matérielle

Utiliser des machines pour explorer les mathématiques est une activité passionnante." Mais le véritable défi réside dans l'utilisation du modèle dans la recherche mathématique, qui est principalement écrit en LaTex, explique Yang-Hui He de l'Institut des sciences mathématiques de Londres. "Nous utilisons LaTex uniquement parce qu'il est facile à taper, mais c'est un langage naturel dans un sens et a ses propres règles."

Il a dit, parce que les utilisateurs peuvent définir leurs propres fonctions et symboles dans LaTeX, ces fonctions et symboles. ne peut être utilisé que dans un seul article de mathématiques, ce qui peut être délicat pour les réseaux de neurones formés uniquement sur du texte brut.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!