Quelles sont les méthodes d'implémentation des fonctions magiques et de la simulation informatique quantique en Python ?

Contexte de simulation de l'informatique quantique

ProjectQ est un cadre de programmation informatique quantique open source très élégant. Ses auteurs originaux sont le Dr Damian et Thomas de l'Institut fédéral suisse de technologie. Ce cadre de programmation d'informatique quantique est un cadre de programmation d'informatique quantique très complet qui est implémenté à partir d'applications d'informatique quantique ->compilation de circuits quantiques ->simulation hamiltonienne ->simulation d'informatique quantique ->amarrage d'API de matériel quantique. Prend en charge l'installation à l'aide de pip : python3 -m pip install projectq --upgrade.

Regardons un exemple d'utilisation de projectq pour simuler l'informatique quantique :

[dechin@dechin-manjaro simulator]$ ipython
Python 3.8.5 (default, Sep  4 2020, 07:30:14) 
Type 'copyright', 'credits' or 'license' for more information
IPython 7.19.0 -- An enhanced Interactive Python. Type '?' for help.
 
In [1]: from projectq import MainEngine
 
In [2]: from projectq.ops import X
 
In [3]: eng = MainEngine()
 
In [4]: qubits = eng.allocate_qureg(2)
 
In [5]: X | qubits[0]
 
In [6]: from projectq.ops import CX
 
In [7]: CX | (qubits[0], qubits[1])
 
In [8]: eng.flush()
 
In [9]: print (eng.backend.cheat()[1])
[0j, 0j, 0j, (1+0j)]

Dans ce cas, nous avons alloué un total de 2 qubits, et les états initiaux de ces 2 bits sont tous des états |0〉 Le vecteur d'amplitude produit par projectq doit être [1, 0, 0, 0]. Les quatre éléments de ce vecteur correspondent aux amplitudes de probabilité des quatre états quantiques 00, 01, 10 et 11 respectivement. Si vous devez calculer la probabilité qu'un certain état soit mesuré, vous devez y effectuer une opération modulo carré. . :

P(00)=(a₀₀+b₀₀i)(a₀₀−b₀₀i)

Notez que l'amplitude de probabilité est un nombre complexe (Complex Number), il doit donc être calculé après la conjugaison, l'opération de produit scalaire est effectuée.

Revenons donc au cas d'utilisation ci-dessus de projectq, dans ce cas, après avoir alloué deux bits, l'opération σ^X de la matrice de Pauli est effectuée sur le premier bit, puis une opération de porte d'intrication CX est effectuée. Ici, les opérations correspondant à l'opération de porte quantique CX(i,j) sont : si le qubit i est dans l'état |0〉, aucune opération n'est effectuée mais si le qubit i est dans l'état |1〉 Opération inverse, c'est-à-dire que si le j original est |0〉, il deviendra |1〉, si le j original est |1〉, il deviendra |0〉. C’est le rôle de l’intrication quantique dans l’informatique quantique, et la mise en œuvre de haute qualité des opérations de portes multi-bits dans les systèmes matériels réels reste un gros problème. La caractéristique de superposition quantique se reflète dans le fait qu'un qubit peut être dans l'état |0〉, ou dans l'état |1〉, ou encore dans un état intermédiaire entre |0〉 sera comme mentionné ci-dessus Pour diviser |0〉 et |1〉 sous forme d'amplitude de probabilité :

P(0)=(a₀+b₀i)⋅(a₀&moins; b₀ i)

P(1)=(a₁+b₁i)⋅(a₁−b₁i)

Ces amplitudes de probabilité peuvent être organisées dans le forme d'un vecteur Levez-vous :

|ψ〉=(a₀+b₀i,a₁+b₁i)^T

Enfin, le nombre d'éléments de ce vecteur augmentera avec le nombre de bits. Le nombre de bits augmente de façon exponentielle. Lorsque le nombre de bits augmente jusqu'à 41, l'espace mémoire requis pour le stockage nécessite plus de 32 To ! Il convient de noter que, comme toutes les amplitudes de probabilité doivent être chargées en mémoire pendant le processus de calcul, cela est différent de l'espace de stockage sur le disque dur. La mémoire à elle seule doit avoir une taille de 32 To ! Par conséquent, utiliser des ordinateurs classiques pour simuler l’informatique quantique est en réalité une méthode très gourmande en ressources. Bien entendu, les simulateurs d’informatique quantique ont toujours leur valeur en recherche. À ce stade, où l’échelle et la qualité des puces quantiques ne peuvent être améliorées, les simulateurs jouent un rôle important.

Implémentation de la fonction magique de Python

Si les lecteurs ont besoin de connaître un plan de mise en œuvre détaillé et complet de la fonction magique de Python, ils peuvent obtenir deux bons articles à partir des liens de référence de cet article. Ici, nous nous concentrons uniquement sur certaines des fonctions qui peuvent être utilisées dans le cas d'utilisation du code projectq ci-dessus : __or__ et __str__, et nous pouvons en faire une simple reproduction.

La fonction magique de Python peut être utilisée pour définir des opérateurs spéciaux pour une classe, tels que l'addition, la soustraction, la multiplication et la division de la classe. Une fois la fonction magique introduite, il n'est pas nécessaire d'opérer les éléments de la classe séparément. mais peut être utilisé. Les fonctions Magic encapsulent les opérations. L'effet final est que nous pouvons utiliser des opérateurs directement dans le code pour opérer sur différentes classes. Par exemple, nous pouvons personnaliser des opérateurs binaires tels que classe1 + classe2. Nous ne le présenterons pas en détail dans ce chapitre. Vous pouvez vous référer aux exemples d'utilisation spécifiques ci-dessous ou à l'article de blog dans le lien.

Définition et implémentation de l'état quantique

Selon l'introduction aux vecteurs d'état quantique dans le premier chapitre, nous pouvons implémenter ici une classe d'état quantique simple. Nous ne pouvons considérer qu'un système simple de deux qubits :

# QubitPair.py
import numpy as np
 
class QubitPair:
    def __init__(self):
        self.state = np.array([1, 0, 0, 0], dtype=complex)
 
    def __str__(self):
        return str(self.state)

Cette définition de. une classe d’état quantique est très simple, c’est une matrice 4×1. Il convient d'ajouter que nous définissons ici une fonction magique de __str__(self), qui est principalement utilisée pour imprimer la représentation sous forme de chaîne de la classe. Par exemple, ici nous convertissons directement le vecteur d'état quantique au format str puis le produisons. Ensuite, si nous imprimons une classe QubitPair personnalisée, la représentation sous forme de chaîne de l'amplitude de probabilité correspondant à la classe actuelle sera affichée.

Définition et implémentation de l'opération de porte quantique

Concernant l'opération de porte quantique, nous pouvons la considérer comme une matrice agissant sur le vecteur d'état quantique. Ici, nous pouvons d'abord montrer la classe Python de l'opération de porte définie, puis la développer :

# Operator.py
import numpy as np
 
class QubitOperator:
    """Pauli rotations and entanglement on qubit-pair"""
    def __init__(self, operation=None, theta=0, index=0):
        self.index = index
        self.name = operation
        paulix = np.array([[0, 1], [1, 0]], dtype=complex)
        pauliy = np.array([[0, -1j], [1j, 0]], dtype=complex)
        pauliz = np.array([[1, 0], [0, -1]], dtype=complex)
        cnot = np.array([[1, 0, 0, 0],
                         [0, 1, 0, 0],
                         [0, 0, 0, 1],
                         [0, 0, 1, 0]])
        if operation == 'X' or operation == 'Rx':
            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*paulix
        elif operation == 'Y' or operation == 'Ry':
            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliy
        elif operation == 'Z' or operation == 'Rz':
            self.operation = np.cos(theta/2)*np.identity(2)-1j*np.sin(theta/2)*pauliz
        elif operation == 'CX' or operation == 'CNOT':
            self.operation = cnot
 
    def __or__(self, qubitpair):
        if self.name == 'CX' or self.name == 'CNOT':
            qubitpair.state = np.dot(self.operation, qubitpair.state)
            return None
        elif self.index == 0:
            operation = np.kron(self.operation, np.identity(2))
        else:
            operation = np.kron(np.identity(2), self.operation)
        qubitpair.state = np.dot(operation, qubitpair.state)

.

Définition de la matrice d'identité et de la matrice de Pauli

这些是基本的泡利矩阵，这三个两能级体系的泡利矩阵具有非常好的物理性质，如都是酉矩阵且存在特殊的对易关系等：

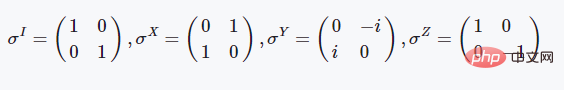
矩阵指数与旋转门操作

矩阵的指数计算一般采用泰勒级数展开的方法来进行定义：

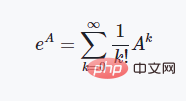
这里如果我们代入上述介绍的泡利矩阵就会得到这样的结果：

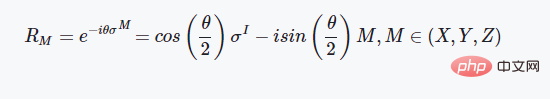
CX门操作的定义

在上述提到的所有的量子门操作中，CX是唯一的一个两比特量子门操作，也就是同时作用在两个量子比特上面，其矩阵形式的定义如下所示：

使用魔法函数__or__来实现量子门操作运算

我们首先简单谈一下为什么要用__or__这个魔法函数而不是其他的二元运算符来实现，这点跟开源库ProjectQ是同步的，理由是我们在量子力学中的运算，一般写成如下的形式：

|ψt〉=U|ψ0〉

将量子态写成狄拉克符号的形式，中文称为"左矢"和"右矢"，英文称之为"bra"和"ket"。因此竖线形式的定义，在形式上会更加契合量子力学的思维，当然，就算是换成其他的符号也是无可厚非的。

功能测试验证

在定义了量子态的类和量子门操作的类之后，我们可以写如下所示的一个测试脚本来测试程序的执行效果：

# TestQubits.py
from QubitPair import QubitPair
from Operator import QubitOperator
 
if __name__ == '__main__':
    qubits = QubitPair()
    print ('The initial state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))

这个程序的测试逻辑为：先定义一个两比特的量子系统，然后对第一个比特执行X门操作，使得其从|0〉态变成|1〉态，再对这两个比特执行纠缠门CX操作，观察其态的变化情况。之后再将第一个比特的状态变回|0〉态，再观察作用CX的态的变化情况，执行结果如下所示：

[dechin@dechin-manjaro simulator]$ python3 TestQubits.py 
The initial state is: [1.+0.j 0.+0.j 0.+0.j 0.+0.j]
Applying X on the 0th qubit...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00-1.j
 0.00000000e+00+0.j]
Applying entanglement on qubits...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
 0.00000000e+00-1.j]
Applying X on the 0th qubit...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]
Applying entanglement on qubits...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]

这个结果所展示出来的数字也许比较乱，这是因为在运算过程中的计算精度不足所导致的，这里低于1e-06的数字其实我们可以认为就是0。那么我们从这个结果中可以分析总结出量子态的演变历程：

|00〉⇒|10〉⇒|11〉⇒|01〉⇒|01〉

注意：上面的这种写法，其实不太合乎程序语言的逻辑，一般从右到左的方向才是从低位到高位的写法。因此，严格来说写法应该是：|00〉⇒|01〉⇒|11〉⇒|10〉⇒|10〉。

这里我们就完成了基于魔法函数的量子计算模拟的过程，感兴趣的读者可以自行尝试更多的玩法，这里就不进行更多的测试了！

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!