Python implémente huit formules de distribution de probabilité et des didacticiels de visualisation de données

La connaissance des probabilités et des statistiques est au cœur de la science des données et de l'apprentissage automatique ; nous avons besoin de connaissances en statistiques et en probabilités pour collecter, examiner et analyser efficacement les données.

Il existe plusieurs exemples de phénomènes dans le monde réel qui sont considérés comme de nature statistique (c'est-à-dire les données météorologiques, les données de ventes, les données financières, etc.). Cela signifie que dans certains cas, nous avons pu développer des méthodes qui nous aident à simuler la nature grâce à des fonctions mathématiques capables de décrire les caractéristiques des données. "Une distribution de probabilité est une fonction mathématique qui donne la probabilité d'occurrence de différents résultats possibles dans une expérience." Comprendre la distribution des données aide à mieux modéliser le monde qui nous entoure. Cela peut nous aider à déterminer la probabilité de divers résultats ou à estimer la variabilité des événements. Tout cela rend la compréhension des différentes distributions de probabilité très précieuse en science des données et en apprentissage automatique. Distribution uniformeLa distribution la plus directe est la distribution uniforme. Une distribution uniforme est une distribution de probabilité dans laquelle tous les résultats sont également probables. Par exemple, si nous lançons un dé juste, la probabilité d’arriver sur n’importe quel nombre est de 1/6. Il s’agit d’une distribution uniforme discrète. Mais toutes les distributions uniformes ne sont pas discrètes : elles peuvent aussi être continues. Ils peuvent prendre n’importe quelle valeur réelle dans la plage spécifiée. La fonction de densité de probabilité (PDF) d'une distribution uniforme continue entre a et b est la suivante : Voyons comment les coder en Python :

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()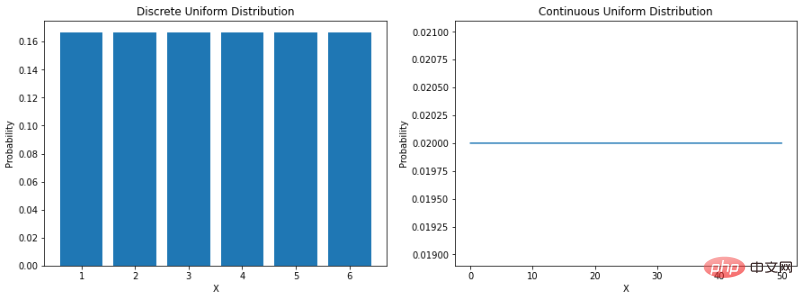

Distribution gaussienne

La distribution gaussienne est probablement la plus couramment entendue et familière. distribution. Elle porte plusieurs noms : certains l'appellent la courbe en cloche parce que son diagramme de probabilité ressemble à une cloche, certains l'appellent la distribution gaussienne parce que le mathématicien allemand Karl Gauss qui l'a décrit le premier l'a nommée, et d'autres encore. Elle est normalement distribuée parce que les premiers statisticiens l'ont remarquée. se produit encore et encore. La fonction de densité de probabilité d'une distribution normale est la suivante : σ est l'écart type et μ est la moyenne de la distribution. Notez que dans une distribution normale, la moyenne, le mode et la médiane sont tous égaux. Lorsque nous traçons une variable aléatoire normalement distribuée, la courbe est symétrique par rapport à la moyenne : la moitié des valeurs sont à gauche du centre et l'autre moitié à droite du centre. Et l’aire totale sous la courbe est de 1.

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()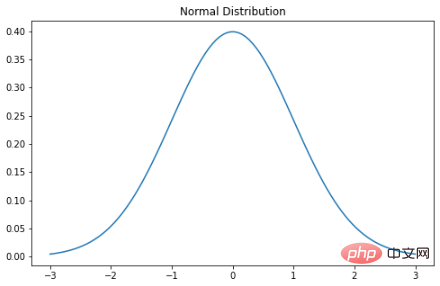

Pour la distribution normale. La règle empirique nous indique quel pourcentage des données se situe dans un certain nombre d’écarts types par rapport à la moyenne. Ces pourcentages sont :

• 68 % des données se situent dans un écart type de la moyenne.
• 95 % des données se situent à moins de deux écarts types de la moyenne.
• 99,7 % des données se situent dans trois écarts types de la moyenne. ​

Distribution lognormale

La distribution lognormale est une distribution de probabilité continue de variables aléatoires avec une distribution lognormale. Par conséquent, si la variable aléatoire X est distribuée de manière log-normale, alors Y = ln(X) a une distribution normale. Voici le PDF de la distribution lognormale : Une variable aléatoire distribuée lognormalement ne prend que des valeurs réelles positives. Par conséquent, la distribution lognormale crée une courbe asymétrique à droite. Traçons-le en Python :

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()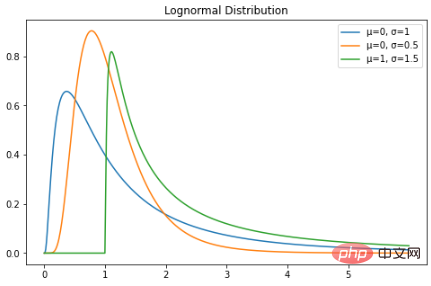

Distribution de Poisson

La distribution de Poisson porte le nom du mathématicien français Simon Denis Poisson. Il s’agit d’une distribution de probabilité discrète, ce qui signifie qu’elle compte les événements ayant des résultats finis – en d’autres termes, il s’agit d’une distribution de comptage. Par conséquent, la distribution de Poisson est utilisée pour montrer le nombre de fois qu'un événement peut se produire au cours d'une période spécifiée. Si un événement se produit à un rythme fixe dans le temps, alors la probabilité d'observer le nombre (n) d'événements dans le temps peut être décrite par une distribution de Poisson. Par exemple, les clients peuvent arriver dans un café à un rythme moyen de 3 fois par minute. Nous pouvons utiliser la distribution de Poisson pour calculer la probabilité que 9 clients arrivent dans les 2 minutes. Voici la formule de la fonction de masse de probabilité : λ est le taux d’événements dans une unité de temps – dans notre cas, il est de 3. k est le nombre d'occurrences - dans notre cas, c'est 9. Scipy peut être utilisé ici pour compléter le calcul de probabilité.

from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3))

0.002700503931560479

La courbe de la distribution de Poisson est similaire à la distribution normale, λ représentant la valeur maximale.

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()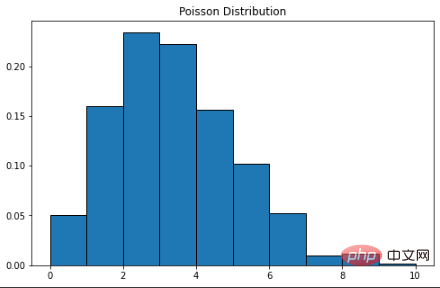

Distribution exponentielle

指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下：λ 是速率参数，x 是随机变量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()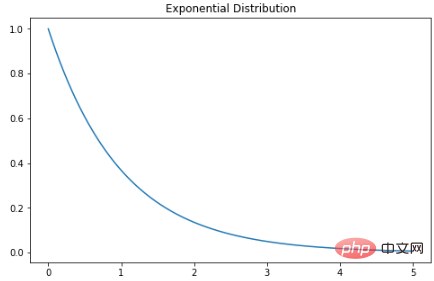

二项分布

可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布，每个实验都问一个是 - 否问题，每个实验都有自己的布尔值结果：成功或失败。本质上，二项分布测量两个事件的概率。一个事件发生的概率为 p，另一事件发生的概率为 1-p。这是二项分布的公式：

• P = 二项分布概率
• = 组合数
• x = n次试验中特定结果的次数
• p = 单次实验中，成功的概率
• q = 单次实验中，失败的概率
• n = 实验的次数

可视化代码如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()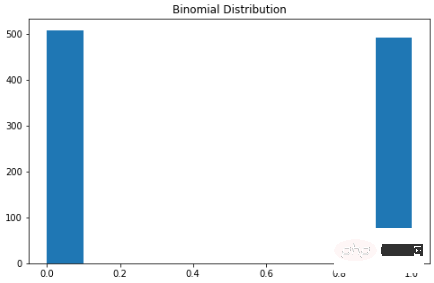

学生 t 分布

学生 t 分布（或简称 t 分布）是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特（William Sealy Gosset）以笔名“student”开发的。PDF如下：n 是称为“自由度”的参数，有时可以看到它被称为“d.o.f.” 对于较高的 n 值，t 分布更接近正态分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()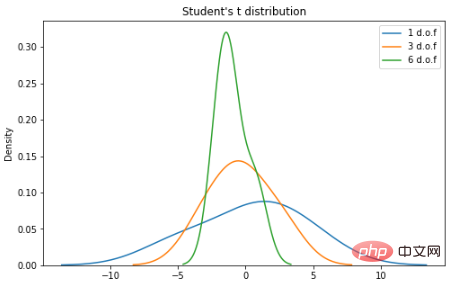

卡方分布

卡方分布是伽马分布的一个特例；对于 k 个自由度，卡方分布是一些独立的标准正态随机变量的 k 的平方和。PDF如下：这是一种流行的概率分布，常用于假设检验和置信区间的构建。在 Python 中绘制一些示例图：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()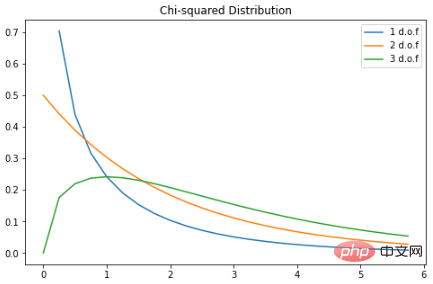

掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布，希望对你有所帮助。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!