Maison >Périphériques technologiques >IA >Modèle quantitatif de calcul parallèle et son application dans un moteur d'apprentissage profond
Modèle quantitatif de calcul parallèle et son application dans un moteur d'apprentissage profond
- 王林avant
- 2023-04-18 13:37:031784parcourir
Parmi les arts martiaux du monde, seuls les arts martiaux rapides sont incassables. Comment former plus rapidement des modèles d'apprentissage profond a été au centre des préoccupations des acteurs de l'industrie, soit en développant du matériel spécial, soit en développant des cadres logiciels, chacun montrant ses capacités uniques.
Bien sûr, ces lois peuvent être vues dans les manuels et la littérature d'architecture informatique, comme cet "Architecture informatique : une approche quantitative", mais la valeur de cet article réside dans son approche ciblée. Sélectionnez les lois les plus fondamentales et combinez-les avec une moteur d’apprentissage profond pour les comprendre.
1 Hypothèses sur la quantité de calcul
Avant d'étudier le modèle quantitatif du calcul parallèle, commençons par quelques réglages. Pour une tâche spécifique de formation du modèle d'apprentissage profond, en supposant que la quantité totale de calcul V est fixe, on peut grossièrement considérer que tant que le calcul de l'ampleur de V est terminé, le modèle d'apprentissage profond terminera la formation.
Cette page GitHub (https://github.com/albanie/convnet-burden) répertorie le montant de calcul requis par les modèles CNN courants pour traiter une image. Il convient de noter que cette page répertorie l'étape suivante. dans la phase de formation nécessite également des calculs dans la phase arrière. Habituellement, la quantité de calculs dans la phase arrière est supérieure à la quantité de calculs avant. Cet article (https://openreview.net/pdf?id=Bygq-H9eg) donne un résultat de visualisation intuitive de la quantité de calcul de traitement d'une image au cours de la phase de formation :
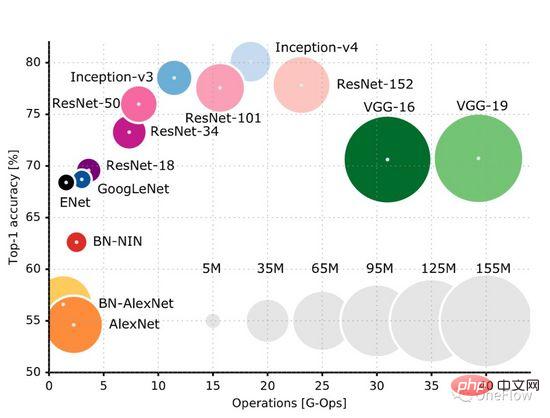
Prenons ResNet-50 comme exemple, La phase de formation nécessite 8G-Ops (environ 8 milliards de calculs) pour traiter une image 224X224x3. L'ensemble des données ImageNet contient environ 1,2 million d'images. Le processus de formation nécessite le traitement de l'ensemble des données 90 fois (estimation approximative, processus de formation). Un total de (8*10^9) *(1,2*10^6)* 90 = 0,864*10^18 opérations sont alors nécessaires. Le montant total de calcul du processus de formation ResNet-50 est d'environ 1 milliard de fois 1 milliard d'opérations. On peut simplement considérer que tant que ces calculs sont terminés, l'opération du modèle est terminée. L’objectif du moteur informatique d’apprentissage profond est d’effectuer cette quantité de calcul donnée dans les plus brefs délais.
2 Hypothèses sur les appareils informatiques
Cet article se limite au dispositif informatique centré sur le processeur (informatique centrée sur le processeur) présenté dans la figure ci-dessous. Le traitement dans les appareils informatiques à mémoire a été exploré dans l'industrie.
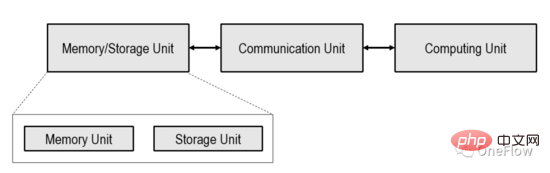
Dans le dispositif informatique présenté dans l'image ci-dessus, l'unité de calcul peut être un processeur à usage général tel qu'un CPU, un GPGPU ou une puce à usage spécial telle qu'un TPU. Si l'unité de calcul est une puce à usage général, les programmes et les données sont généralement stockés dans l'unité de mémoire, qui est également l'ordinateur à structure von Neumann le plus populaire aujourd'hui.
Si l'unité de calcul est une puce dédiée, seules les données sont généralement stockées dans l'unité de mémoire. L'unité de communication est responsable du transfert des données de l'unité de mémoire vers l'unité de calcul et de l'achèvement du chargement des données. Une fois que l'unité de calcul a obtenu les données, elle est responsable de l'achèvement du calcul (conversion des données). les résultats du calcul à l’unité de mémoire pour terminer le stockage des données (Store).
La capacité de transmission de l'unité de communication est généralement exprimée par la bande passante d'accès à la mémoire bêta, c'est-à-dire le nombre d'octets pouvant être transférés par seconde, qui est généralement lié au nombre de câbles et à la fréquence du signal. La puissance de calcul d'une unité de calcul est généralement représentée par le débit pi, qui est le nombre de calculs à virgule flottante (flops) pouvant être effectués par seconde. Ceci est généralement lié au nombre de dispositifs informatiques logiques intégrés sur l'ordinateur. l’unité et la fréquence d’horloge.
L'objectif du moteur d'apprentissage profond est de maximiser les capacités de traitement des données de l'appareil informatique grâce à la co-conception logicielle et matérielle, c'est-à-dire d'effectuer une quantité donnée de calculs dans les plus brefs délais.
3 Roofline Model : Un modèle mathématique qui décrit les performances informatiques réelles
Les performances informatiques réelles (nombre d'opérations terminées par seconde) qu'un appareil informatique peut atteindre lors de l'exécution d'une tâche ne sont pas seulement liées à la bande passante d'accès à la mémoire bêta et à la pic théorique pi de l'unité de calcul Il est également lié à l'intensité arithmétique (ou intensité opérationnelle) de la tâche en cours elle-même.
L'intensité de calcul d'une tâche est définie comme le nombre de calculs en virgule flottante requis par octet de données, c'est-à-dire des flops par octet. Généralement compris, une tâche avec une faible intensité de calcul signifie que l'unité de calcul doit effectuer moins d'opérations sur un octet transporté par l'unité de communication. Afin de garder l'unité de calcul occupée dans ce cas, l'unité de communication doit fréquemment transporter des données ; Une tâche avec une intensité de calcul élevée signifie que l'unité de calcul doit effectuer plus d'opérations sur un octet transféré par l'unité de communication. L'unité de communication n'a pas besoin de transférer des données aussi fréquemment pour maintenir l'unité de calcul occupée.
Tout d'abord, les performances informatiques réelles ne dépasseront pas le pic théorique pi de l'unité de calcul. Deuxièmement, si la bande passante d'accès à la mémoire bêta est très faible, seuls les octets bêta peuvent être transférés de la mémoire vers l'unité de calcul en 1 seconde. Soit je représente le nombre d'opérations requises pour chaque octet dans la tâche informatique en cours, alors bêta * I. représente 1 seconde. Le nombre réel d'opérations nécessaires pour transférer des données dans une horloge. Si bêta * I
Le modèle Roofline est un modèle mathématique qui déduit les performances informatiques réelles en fonction de la relation entre la bande passante d'accès à la mémoire, le débit de pointe de l'unité de calcul et l'intensité de calcul de la tâche. Publié par l'équipe de David Patterson sur les communications d'ACM en 2008 (https://en.wikipedia.org/wiki/Roofline_model), il s'agit d'un modèle visuel simple et élégant :
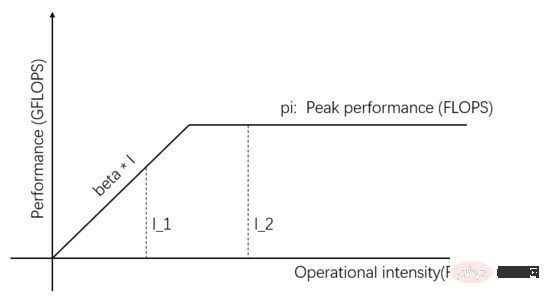
Figure 1 : Modèle de ligne de toit
L'indépendant les variables sur l'axe horizontal de la figure 1 représentent l'intensité de calcul des différentes tâches, c'est-à-dire le nombre d'opérations en virgule flottante requises par octet. La variable dépendante sur l'axe vertical représente les performances de calcul réellement réalisables, c'est-à-dire le nombre d'opérations en virgule flottante effectuées par seconde. La figure ci-dessus montre les performances de calcul réelles qui peuvent être obtenues par deux tâches avec une intensité de calcul I_1 et I_2. L'intensité de calcul de I_1 est inférieure à pi/bêta, ce qui est appelé tâche à accès mémoire limité. Les performances de calcul réelles bêta * I_1. est inférieur au pic théorique pi .
L'intensité de calcul de I_2 est supérieure à pi/bêta, ce que l'on appelle une tâche informatique limitée. Les performances de calcul réelles atteignent le pic théorique pi, et la bande passante d'accès à la mémoire utilise uniquement pi/(I_2*bêta). La pente de la figure sur la figure est bêta. L'intersection de la pente et de la ligne horizontale du pic théorique pi est appelée point de crête. L'abscisse du point de crête est pi/bêta. pi/beta, l'unité de communication. Elle est dans un état équilibré avec l'unité de calcul, et aucune n'est gaspillée.
Rappelons que l'objectif du moteur d'apprentissage profond est de « réaliser une quantité donnée de calculs dans les plus brefs délais », ce qui est de maximiser les performances de calcul réellement réalisables du système. Pour atteindre cet objectif, plusieurs stratégies sont disponibles.
I_2 sur la figure 1 est une tâche limitée par le calcul. Les performances de calcul réelles peuvent être améliorées en augmentant le parallélisme de l'unité de calcul et en augmentant ainsi la valeur maximale théorique, par exemple en intégrant davantage d'unités arithmétiques et logiques (ALU) sur l'unité de calcul. Spécifique aux scénarios de deep learning, il s’agit d’ajouter des GPU, d’un GPU à plusieurs GPU fonctionnant en même temps.
Comme le montre la figure 2, lorsque davantage de parallélisme est ajouté au sein de l'unité de calcul, la valeur maximale théorique est supérieure à la bêta * I_2, alors les performances de calcul réelles de I_2 sont plus élevées et ne nécessitent que moins de temps.
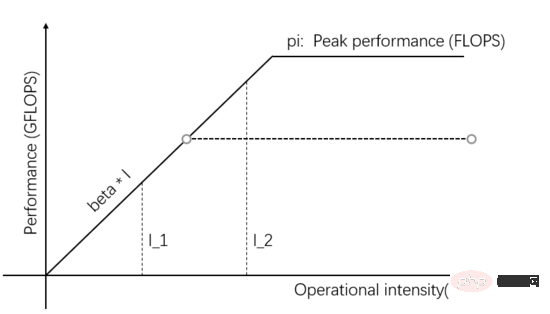
Figure 2 : Augmentez la valeur maximale théorique de l'unité de calcul pour améliorer les performances de calcul réelles
I_1 dans la figure 1 est une tâche à accès mémoire limité, vous pouvez améliorer les performances de calcul réelles en améliorant la bande passante de transmission de l’Unité de Communication. Améliorer les capacités de fourniture de données. Comme le montre la figure 3, la pente de la pente représente la bande passante de transmission de l'unité de communication. Lorsque la pente de la pente augmente, I_1 passe d'une tâche à accès mémoire limité à une tâche à calcul limité, et les performances de calcul réelles sont. amélioré.
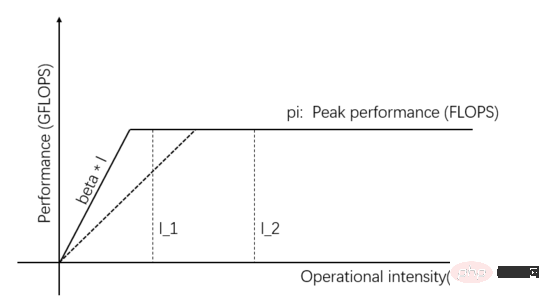
Figure 3 : Améliorer la capacité d'alimentation en données de l'unité de communication pour améliorer les performances informatiques réelles
En plus d'améliorer les performances informatiques réelles en améliorant la bande passante de transmission ou la valeur maximale théorique du matériel, elle peut également être améliorée en améliorant l'intensité de calcul de la tâche elle-même. Performances de calcul réelles. La même tâche peut être implémentée de différentes manières, et l’intensité de calcul des différentes implémentations diffère également. Une fois que l'intensité de calcul est transformée de I_1 pour dépasser pi/bêta, cela devient une tâche informatique limitée et les performances de calcul réelles atteignent pi, dépassant la bêta*I_1 d'origine.
Dans les moteurs d'apprentissage profond réels, les trois méthodes ci-dessus (augmentation du parallélisme, amélioration de la bande passante de transmission et utilisation d'algorithmes avec une meilleure intensité de calcul) sont toutes utilisées.
4 Loi d'Amdahl : Comment calculer le taux d'accélération ?
L'exemple de la figure 2 améliore les performances de calcul réelles en augmentant le parallélisme de l'unité de calcul. Dans quelle mesure le temps d'exécution de la tâche peut-il être raccourci ? C'est la question du taux d'accélération, c'est-à-dire que l'efficacité est augmentée plusieurs fois.
Pour faciliter la discussion, (1) nous supposons que la tâche actuelle est limitée sur le plan informatique, permettez-moi de représenter l'intensité de calcul, c'est-à-dire I*beta>pi. Après avoir augmenté l'unité de calcul de l'unité de calcul de s fois, le pic de calcul théorique est s * pi. Supposons que l'intensité de calcul I de la tâche soit suffisamment élevée pour qu'après que la valeur du pic théorique ait été augmentée de s fois, elle soit toujours. limité en termes de calcul, c'est-à-dire I*beta > s*pi ; (2) En supposant qu'aucun pipeline n'est utilisé, l'unité de communication et l'unité de calcul sont toujours exécutées séquentiellement (nous discuterons spécifiquement de l'impact du pipeline plus tard). Calculons combien de fois l'efficacité de l'exécution des tâches s'est améliorée.
Dans la situation initiale où la valeur maximale théorique est pi, l'unité de communication transfère les octets bêta de données en 1 seconde et l'unité de calcul a besoin de (I*beta)/pi secondes pour terminer le calcul. Autrement dit, le calcul de I*beta est effectué en 1+(I*beta)/pi secondes, puis le calcul de (I*beta) / (1 + (I*beta)/pi) peut être effectué par unité de temps. , en supposant que le total La quantité de calcul est V, cela prend donc t1=V*(1+(I*beta)/pi)/(I*beta) secondes au total.
Après avoir augmenté le pic de calcul théorique de s fois en augmentant le parallélisme, l'unité de communication a encore besoin de 1 seconde pour transférer les octets bêta de données, et l'unité de calcul a besoin de (I*beta)/(s*pi) secondes pour terminer le calcul. En supposant que le montant total du calcul est V, il faut t2=V*(1+(I*beta)/(s*pi))/(I*beta) secondes pour terminer la tâche.
Calculez t1/t2 pour obtenir le rapport d'accélération : 1/(pi/(pi+I*beta)+(I*beta)/(s*(pi+I*beta))). est moche, lecteurs. Vous pouvez le dériver vous-même, c'est relativement simple.
Lorsque la valeur maximale théorique est pi, il faut 1 seconde pour transférer les données et (I*beta)/pi secondes pour calculer. Ensuite, la proportion du temps de calcul est (I*beta)/(pi + I*beta). Soit p représente ce rapport, égal à (I*beta)/(pi + I*beta).
En remplaçant p dans le rapport d'accélération de t1/t2, vous pouvez obtenir le rapport d'accélération sous la forme 1/(1-p+p/s). C'est la célèbre loi d'Amdahl ( https://en.wikipedia.org/wiki). /Amdahl%27s_law). Où p représente la proportion de la tâche d'origine qui peut être parallélisée, s représente le multiple de parallélisation et 1/(1-p+p/s) représente l'accélération obtenue.
Utilisons un nombre simple pour calculer. Supposons que l'unité de communication prend 1 seconde pour transférer les données et que l'unité de calcul prend 9 secondes pour calculer, alors p = 0,9. Supposons que nous améliorions le parallélisme de l’unité de calcul et augmentions sa valeur maximale théorique de 3 fois, c’est-à-dire s=3. L’unité de calcul ne prend alors que 3 secondes pour terminer le calcul. Alors, quel est le taux d’accélération ? En utilisant la loi d'Amdahl, nous pouvons savoir que le rapport d'accélération est de 2,5 fois et que le rapport d'accélération de 2,5 est inférieur au multiple de parallélisme de 3 de l'unité de calcul.
Nous avons goûté à la douceur d'augmenter le parallélisme de l'unité de calcul. Pouvons-nous obtenir un meilleur taux d'accélération en augmentant encore le parallélisme ? Peut. Par exemple, si s = 9, alors nous pouvons obtenir un rapport d’accélération de 5x et nous pouvons voir que les avantages d’un parallélisme croissant deviennent de plus en plus faibles.
Pouvons-nous augmenter le taux d'accélération en augmentant s à l'infini ? Oui, mais cela devient de moins en moins rentable. Imaginez simplement que si s tend vers l'infini (c'est-à-dire si la valeur maximale théorique de l'unité de calcul est infinie), p/s tendra vers 0, alors l'accélération maximale. le rapport est 1/(1-p)=10.
Tant qu'il y a une partie non parallélisable (unité de communication) dans le système, le rapport d'accélération ne peut pas dépasser 1/(1-p).
La situation réelle peut être pire que la limite supérieure du rapport d'accélération 1/(1-p), car l'analyse ci-dessus suppose que l'intensité de calcul I est infinie, et en augmentant le parallélisme de l'unité de calcul, la bande passante de transmission de l'unité de communication diminuera généralement. Cela rend p plus petit, donc 1/(1-p) est plus grand.
Cette conclusion est très pessimiste. Même si la surcharge de communication (1-p) ne représente que 0,01, cela signifie que peu importe le nombre d'unités parallèles utilisées, des dizaines de milliers, nous ne pouvons obtenir qu'une accélération maximale de 100 fois. Existe-t-il un moyen de rendre p aussi proche que possible de 1, c'est-à-dire que 1-p se rapproche de 0, améliorant ainsi le rapport d'accélération ? Il existe une solution miracle : la chaîne de montage.
5 Pipelining : Panacée
Lors de la dérivation de la loi d'Amdahl, nous avons supposé que l'unité de communication et l'unité de calcul fonctionnent en série. L'unité de communication est toujours envoyée pour transférer les données en premier, et l'unité de calcul est ensuite calculée une fois le calcul terminé. terminé, l'unité de communication est transférée aux données à nouveau, et ainsi de suite.
L'unité de communication et l'unité de calcul peuvent-elles fonctionner en même temps, transférer des données et calculer en même temps ? Si l'unité de calcul peut immédiatement commencer à calculer le prochain lot de données après avoir calculé une donnée, alors p sera presque 1. Quel que soit le nombre de fois où le degré de parallélisme s est augmenté, un rapport d'accélération linéaire peut être obtenu. Examinons les conditions dans lesquelles une accélération linéaire peut être obtenue.
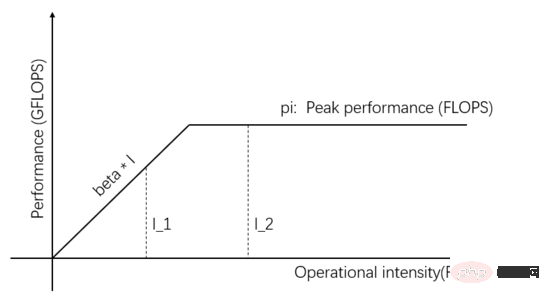
Figure 4 : (Identique à la figure 1) Le modèle de ligne de toit
I_1 dans la figure 4 est une tâche limitée en communication. L'unité de communication peut transporter des octets bêta de données en 1 seconde, et l'unité informatique doit les traiter. octets bêta. La quantité de calcul est constituée d'opérations bêta*I_1, le pic de calcul théorique est de pi et il faut un total de (bêta*I_1)/pi secondes pour terminer le calcul.
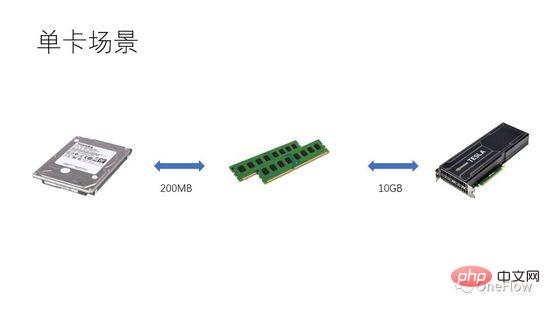
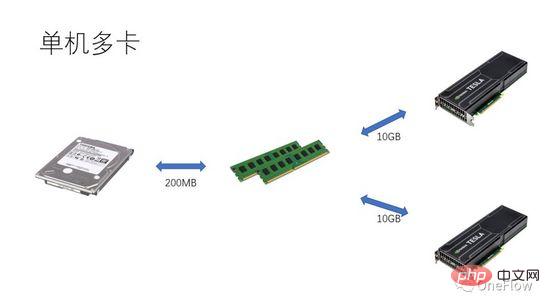
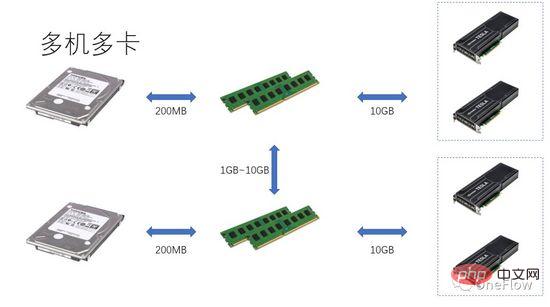
Pour les tâches limitées en communication, nous avons beta*I_1 I_2 sur la figure 4 est une tâche limitée en termes de calcul. L'unité de communication peut transférer des octets bêta de données en 1 seconde. La quantité de calcul requise par l'unité de calcul pour traiter ces octets bêta est la valeur de calcul théorique. est pi. Il faut un total de (beta*I_2)/pi secondes pour terminer le calcul. Pour les tâches limitées en calcul, nous avons beta*I_2>pi, donc le temps de calcul de l'unité de calcul est supérieur à 1 seconde. Cela signifie également qu'il faut plusieurs secondes pour terminer le calcul des données dont le transfert prend 1 seconde. Il y a suffisamment de temps pour transférer le prochain lot de données dans le temps de calcul, ce qui signifie que le temps de calcul peut couvrir le temps de calcul. temps de transfert de données. Le maximum p est 1. Tant que I est infini, le rapport d'accélération peut être infini. La technologie qui permet à l'unité de communication et à l'unité informatique de se chevaucher et de fonctionner est appelée pipeline (Pipeling : https://en.wikipedia.org/wiki/Pipeline_(computing)). Il s'agit d'une technologie qui améliore efficacement l'utilisation de l'unité de calcul et améliore le taux d'accélération. Les différents modèles quantitatifs évoqués ci-dessus sont également applicables au développement de moteurs d'apprentissage profond, par exemple, pour les tâches limitées en calcul, il peut être accéléré en augmentant la vitesse. degré de parallélisme (ajout de cartes graphiques) Même si le même périphérique matériel est utilisé, l'utilisation de différentes méthodes parallèles (parallélisme des données, parallélisme des modèles ou parallélisme des pipelines) affectera l'intensité de calcul I, affectant ainsi les performances de calcul réelles ; Le moteur contient une grande quantité de frais généraux de communication et de temps d'exécution, la manière de réduire ou de masquer ces frais généraux est essentielle à l'effet d'accélération. Comprenant le modèle d'apprentissage profond basé sur la formation GPU du point de vue d'un appareil informatique centré sur le processeur, les lecteurs peuvent réfléchir à la façon de concevoir un moteur d'apprentissage profond pour obtenir un meilleur taux d'accélération. Dans le cas d'une seule machine et d'une seule carte, il vous suffit de compléter le pipeline de transfert de données et de calcul pour atteindre 100 % d'utilisation du GPU. Les performances informatiques réelles dépendent en fin de compte de l'efficacité du calcul matriciel sous-jacent, c'est-à-dire de l'efficacité de cudnn. En théorie, il ne devrait y avoir aucun écart de performances entre les différents cadres d'apprentissage profond dans un scénario à carte unique. Si vous souhaitez gagner en accélération en ajoutant des GPU au sein de la même machine, par rapport au scénario à carte unique, la complexité du transfert de données entre les GPU augmente et différentes méthodes de division des tâches peuvent produire une intensité de calcul différente (I). Par exemple, les couches convolutives conviennent au parallélisme des données et les couches entièrement connectées conviennent au parallélisme des modèles). En plus de la surcharge de communication, la surcharge de planification d’exécution affecte également l’accélération. Dans les scénarios multi-machines et multi-cartes, la complexité du transfert de données entre GPU est encore accrue. La bande passante du transfert de données entre les machines via le réseau est généralement inférieure à la bande passante du transfert de données via PCIe au sein de la machine. , ce qui signifie que le degré de parallélisme est augmenté, mais la bande passante de transfert de données a été réduite, ce qui signifie que la pente de la pente dans le modèle Roofline est devenue plus petite. Les scénarios tels que CNN qui conviennent au parallélisme des données signifient généralement relativement. une intensité de calcul I élevée, et il existe certains modèles tels que RNN/LSTM, où l'intensité de calcul I est beaucoup plus faible, ce qui signifie également que la surcharge de communication dans le pipeline est plus difficile à dissimuler. Les lecteurs qui ont utilisé des moteurs d'apprentissage profond distribués devraient avoir une expérience personnelle du taux d'accélération du cadre logiciel. Fondamentalement, les réseaux de neurones convolutifs, un modèle adapté au parallélisme des données (avec une intensité de calcul I relativement élevée), sont. amélioré en augmentant L'effet d'accélération du GPU est tout à fait satisfaisant. Cependant, il existe un grand type de réseau neuronal qui utilise le parallélisme de modèle, qui a une intensité de calcul plus élevée, et même s'il utilise le parallélisme de modèle, son intensité de calcul est bien inférieure à celle-là. des réseaux de neurones convolutifs. La façon dont ces applications peuvent être accélérées en augmentant le parallélisme GPU est un problème non résolu dans l'industrie. Dans les évaluations précédentes d'apprentissage en profondeur, il est même arrivé que l'utilisation de plusieurs GPU pour entraîner RNN soit plus lente qu'un seul GPU ( https://rare-technologies.com/machine-learning-hardware-benchmarks/ ). Quelle que soit la technologie utilisée pour résoudre le problème d'efficacité du moteur d'apprentissage profond, elle reste la même. Afin d'améliorer le taux d'accélération, il s'agit de réduire la surcharge d'exécution, de choisir un mode parallèle approprié pour augmenter l'intensité de calcul et de masquer. frais généraux de communication via des pipelines. Dans le cadre couvert par les lois fondamentales décrites dans cet article. 6 L'inspiration du modèle quantitatif de calcul parallèle pour les moteurs d'apprentissage profond
7 Résumé
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

