Maison >Périphériques technologiques >IA >Analyse de la technologie de positionnement global basée sur des points caractéristiques de la conduite autonome
Analyse de la technologie de positionnement global basée sur des points caractéristiques de la conduite autonome
- 王林avant
- 2023-04-12 15:19:431686parcourir
Dans la conduite autonome, la perception, le positionnement, la planification et la prise de décision, ainsi que le contrôle sont les quatre modules de base du système. Étant donné que l’algorithme actuel ne peut pas atteindre une intelligence absolue, une grande quantité de connaissances préalables est encore nécessaire pour améliorer les performances et la robustesse des modules afin d’obtenir une conduite autonome sûre. Parmi eux, les cartes de haute précision intègrent des connaissances préalables sur les routes et les environnements environnants. Le positionnement précis basé sur la carte constitue une base importante pour évaluer les conditions de conduite et fournit un soutien solide pour les décisions ultérieures en matière de perception et de planification.
Les principales sources de données utilisées pour le positionnement comprennent actuellement le GPS, le lidar, la vision et le radar à ondes millimétriques. Pour la vision, bien qu'il n'existe actuellement aucune solution de positionnement suffisamment fiable et reconnue dans l'industrie, l'exploration dans ce domaine ne s'est jamais arrêtée. Les principales raisons sont les suivantes :
La sécurité est l'indicateur le plus important des systèmes de conduite sans pilote, donc la mise en œuvre. L'une des principales fonctions est le couplage de données multi-sources et de différents résultats d'algorithmes. Aucune solution de capteur n'est parfaite. Par exemple, le GPS RTK, en tant que solution largement utilisée, est facilement affecté par les conditions météorologiques et les conditions de transmission des liaisons de données, et ne peut pas être utilisé dans les tunnels, à l'intérieur et dans les zones densément peuplées avec des immeubles de grande hauteur. De plus, bien que le lidar présente l'avantage d'une faible charge de travail de calcul, fournit des informations sur la profondeur et n'est pas affecté par l'éclairage, les informations sont rares, le coût reste très élevé et il n'a pas encore la capacité d'assembler de grandes quantités de véhicules. En comparaison, bien que les informations visuelles fournies par les caméras soient affectées par l’éclairage et la météo, elles sont peu coûteuses et riches en contenu. Elles constituent la principale source de données pour les solutions de conduite assistée actuelles et présentent également un grand potentiel en matière de positionnement cartographique.
Étant donné que les idées fondamentales des algorithmes de positionnement visuel traditionnels sont les mêmes, cet article présente uniquement l'algorithme de positionnement global le plus couramment utilisé basé sur des points caractéristiques dans la pratique du point de vue d'une série de composants importants du cadre d'algorithme, c'est-à-dire dans le système de coordonnées de la carte À positionner. Cet article omet la dérivation de la formule d'optimisation et de contrainte géométrique impliquée, dans le but de donner aux étudiants une introduction macro à l'algorithme de positionnement. Pour des détails spécifiques, veuillez vous référer à la littérature et aux livres pertinents.
1 Concept de positionnement global visuel
Le positionnement global visuel fait référence à la recherche de la pose (Pose) à 6 degrés de liberté (DoF) de la caméra dans le système de coordonnées cartographiques en fonction de l'image actuelle, c'est-à-dire le (x, y, z) et les déviations angulaires (lacet, tangage, roulis) autour des trois axes de coordonnées. À l’heure actuelle, elles peuvent être principalement classées en méthodes basées sur la structure 3D, méthodes basées sur des images 2D, méthodes basées sur des images séquentielles et méthodes basées sur l’apprentissage profond. Parmi elles, les méthodes basées sur l'apprentissage en profondeur sont des méthodes de bout en bout, tandis que d'autres méthodes non de bout en bout à plusieurs étapes (multi-étapes) ont des processus différents, mais les idées de l'algorithme sont pour la plupart celles illustrées dans la figure 1. Représentation :

Figure 1 : Sur la base de l'image de requête, calculez la matrice de transformation 2D-3D et résolvez la pose de la caméra
Sur la base de la carte construite, faites correspondre le sous-ensemble de carte le plus similaire de l'histoire (image/nuage de points/point caractéristique), sur la base de la véritable valeur de pose historique et de la valeur réelle des coordonnées du point caractéristique fournies par le sous-ensemble de carte correspondant, calculez la matrice de transformation entre les paires de points et résolvez la pose actuelle de la caméra.
Ainsi, son noyau comprend quatre aspects : la description de l'image, la requête de cartographie, la correspondance des caractéristiques et le calcul de la pose. Il ne s'agit que d'une macro-classification au niveau technique. Le cadre algorithmique actuel n'est pas nécessairement exécuté dans cet ordre, et les chercheurs se concentrent principalement sur l'amélioration de ces technologies dans leurs recherches. Dans l’ensemble, la description d’image basée sur les points caractéristiques est fondamentalement mature et moins développée. Le calcul de pose étant un problème d’optimisation basé sur des contraintes géométriques, la méthode est relativement figée. En revanche, il existe de nombreuses techniques améliorées en matière de requêtes de mappage et de correspondance de fonctionnalités. Selon la source de données, la requête de mappage et la correspondance peuvent être 2D-2D, 2D-3D ou 3D-3D. Les images 2D sont obtenues par des caméras et des nuages de points 3D peuvent être générés par des caméras binoculaires ou des caméras RVB-D qui fournissent de la profondeur.
2 Extraction des points caractéristiques
L'image 2D elle-même est une matrice composée de luminosité et de couleur. Elle est très sensible à l'angle de vue, à l'éclairage, aux changements de teinte, etc., et il est très difficile de l'utiliser directement. Par conséquent, des points représentatifs sont généralement utilisés pour les calculs pertinents. Les gens espèrent que de tels points présentent les avantages de la rotation, de la translation, de l'échelle, de l'invariance de l'éclairage, etc. Ces points sont appelés points caractéristiques de l'image, comprenant les points clés et les descripteurs. Les points clés expriment l'emplacement des points caractéristiques, tandis que les descripteurs décrivent les caractéristiques visuelles des points caractéristiques, principalement sous forme vectorielle. De manière générale, les descripteurs comptent principalement les changements d'échelle de gris/dégradé de couleur autour des points clés d'un certain motif. Pour un descripteur robuste, la distance (Distance) du descripteur du même point caractéristique doit être plus petite dans différentes situations d'images différentes.
Les descripteurs sont généralement des fonctionnalités créées à la main. Les descriptions classiques incluent HOG (Histogramme de gradients orientés) [1], SIFT (Transformation de caractéristiques invariantes à l'échelle) [2], SURF (Fonctionnalités robustes accélérées) [3], AKAZE (KAZE accéléré) [4], etc.
Afin de répondre aux exigences du temps réel, certains descripteurs de modèles binaires avec une vitesse de calcul plus rapide ont été conçus, tels que LBP (Local Binary Patterns) [5], BRIEF (Binary Robust Independent Elementary Features), ORB (Oriented FAST et rotation BRIEF)[6], BRISK(Binary robuste invariant scalable key-point)[7], FREAK(Fast retina key-point)[8], etc.
Avant que l'apprentissage profond ne devienne populaire, ces fonctionnalités conçues à la main étaient à la pointe de l'ensemble du secteur de la vision informatique. À ce jour, ces fonctionnalités sont encore largement utilisées dans des scénarios manquant de données étiquetées et comportant de nombreuses contraintes. Ce qui suit est une brève introduction à deux descripteurs couramment utilisés.
SIFT
Le descripteur SIFT peut être considéré comme l'une des technologies les plus influentes dans le monde du CV. Au niveau de la détection des points clés, la méthode Différence de Gauss (DoG) est principalement utilisée pour détecter des points extrêmes sur un espace multi-échelle en tant que points clés. Babaud et al. [9] ont prouvé que le lissage gaussien est le seul noyau de filtre de lissage spatial multi-échelle pouvant être utilisé, fournissant un support théorique suffisant pour les méthodes associées.
Alors pourquoi une telle méthode peut-elle trouver les points clés des caractéristiques ?
Parce que le noyau gaussien peut redimensionner l'image à différents espaces d'échelle grâce au flou et aux valeurs des zones lisses avec de petits changements de dégradé dans différents espaces d'échelle. L'écart est plus petit. Au contraire, les différences sont plus importantes dans des zones telles que les bords, les points, les coins et les textures. De cette façon, en faisant des différences entre des images d'échelles adjacentes, les points extrêmes de l'espace multi-échelle peuvent enfin être calculés. Cependant, les différents détails de l’image se situent intrinsèquement à des échelles différentes. Par exemple, dans un portrait, le visage peut être lissé en un seul morceau après un léger flou, tandis que les coins du cadre peuvent nécessiter un lissage à plus grande échelle pour refléter les « valeurs extrêmes » locales.
Par conséquent, comme le montre la figure 2, les images sont d'abord regroupées (Octave) à l'aide de la pyramide d'images, et des noyaux gaussiens de différentes échelles sont utilisés dans chaque groupe pour former une série de couches. Cette méthode est meilleure que la simple utilisation de plus d'échelles de noyaux gaussiens et peut détecter plus de points caractéristiques. Il convient de noter que bien que SIFT utilise DoG pour la détection des points clés, d'autres méthodes de détection sont également réalisables et n'affectent pas l'établissement des descripteurs SIFT.
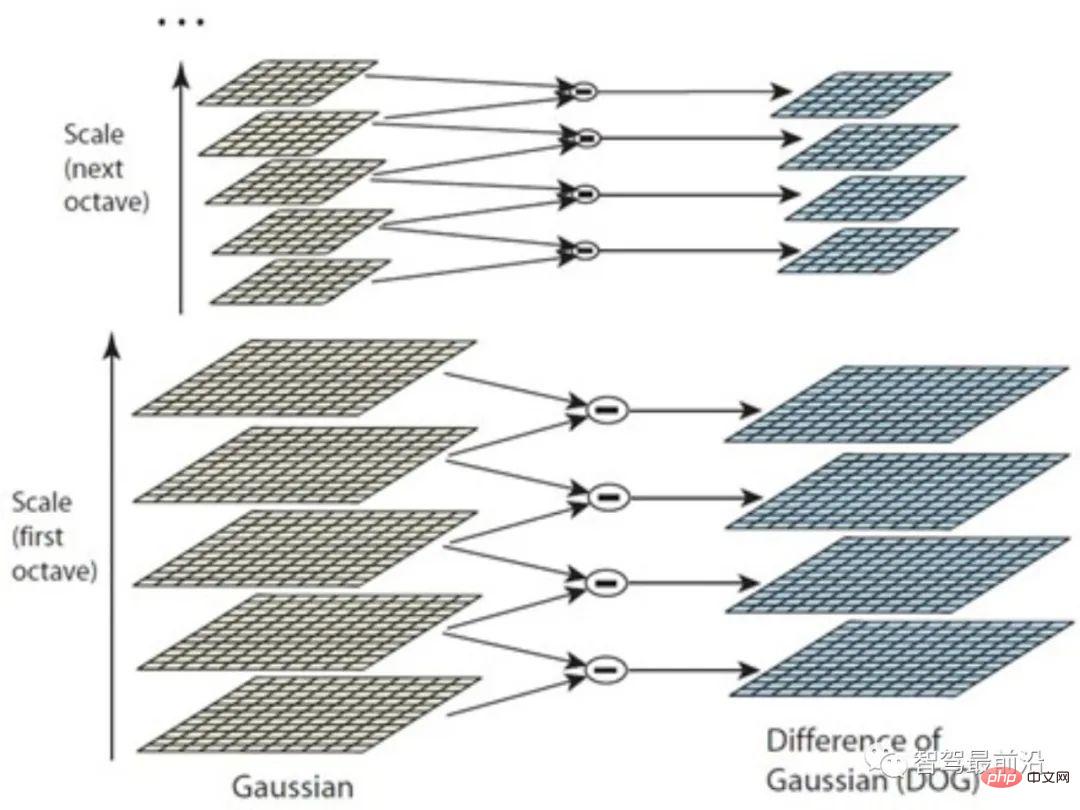
Figure 2 : Méthode de différence gaussienne
Le descripteur de point caractéristique SIFT peut être compris comme une simple version statistique de HOG. Comme le montre la figure 3, avec le point clé détecté comme centre, une zone environnante de 16 × 16 est sélectionnée et la zone est réorganisée en quatre patchs 4 × 4. Pour chaque bloc, un histogramme à 8 cases est utilisé pour compter les dégradés. La direction du dégradé détermine dans quelle case il tombe et le module du dégradé détermine la taille de la valeur. Afin de garantir la cohérence de l’échelle, la taille du dégradé doit être normalisée. Afin de garantir l'invariance de la rotation, une direction principale est calculée sur la base de tous les gradients dans la zone 16 × 16, et tous les gradients sont pivotés selon la direction principale. Le résultat est un vecteur de 128 dimensions 4 × 4 × 8.
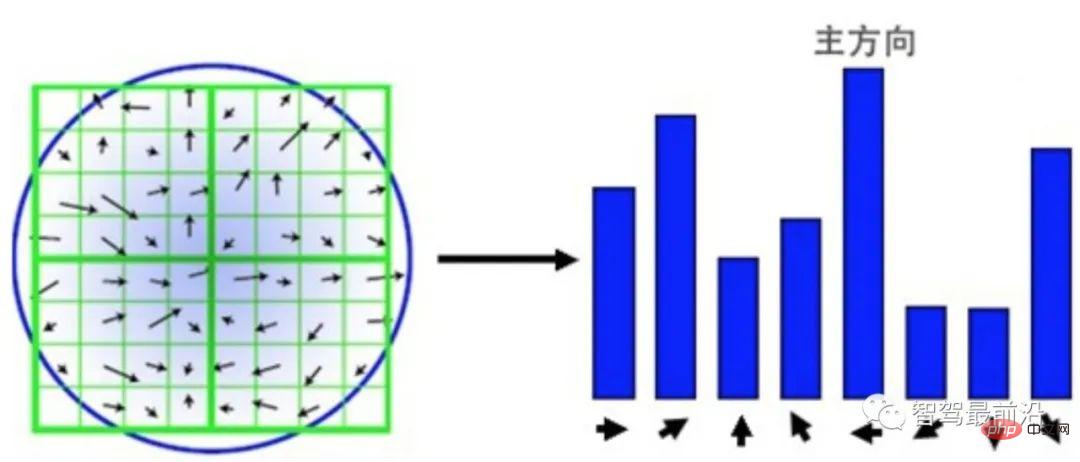
Figure 3 : Descripteur SIFT basé sur les statistiques des blocs de gradient
Descripteur binaire
Bien que certains algorithmes améliorés aient été produits après la proposition de SIFT Tels que SURF, AKAZE , etc., mais même aujourd'hui en 2019, il est encore difficile de garantir les exigences en temps réel de l'algorithme dans certains scénarios. Par exemple, les appareils portables ont généralement une puissance de calcul limitée. En conduite autonome, les ressources CPU et GPU doivent être planifiées simultanément par plusieurs modules gourmands en calcul. L’efficacité est donc un indicateur important pour examiner la praticité d’un algorithme.
Afin d'améliorer l'efficacité, certains descripteurs binaires ont été proposés par des chercheurs. Généralement, ces méthodes effectuent un échantillonnage de points autour des points clés des caractéristiques. Ensuite, la taille en niveaux de gris d'une paire de points est comparée et le résultat est exprimé sous la forme 0/1, formant un vecteur de description binaire à N dimensions, formant un motif binaire de points caractéristiques. La plus grande différence entre les différents descripteurs binaires réside principalement dans les différents modes d'échantillonnage de caractéristiques et les différentes méthodes de sélection de paires de points.
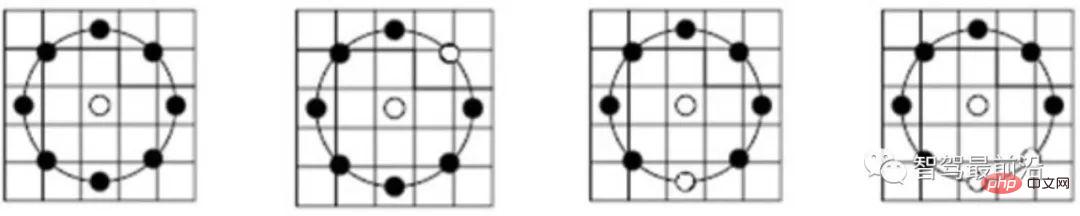
Figure 4 : Mode de sous-échantillonnage du descripteur LBP
Comme le montre la figure 4, le descripteur LBP adopte un échantillonnage circulaire autour du point clé et le compare avec l'échelle de gris du point clé central Options comparatives . Les résultats de la comparaison en niveaux de gris sont affichés sur l'anneau, les points noirs étant 0 et les points blancs étant 1. LBP est la forme la plus simple de descripteur binaire, tandis que ORB améliore la fonctionnalité BRIEF et est actuellement un descripteur binaire couramment utilisé. Comme le montre la figure 5, lors de la sélection de paires de points, ORB utilise une méthode aléatoire pour décrire les détails locaux de manière plus complète, contrairement à la simple utilisation du point central. Cependant, la corrélation entre les paires de points sera relativement importante, réduisant ainsi le caractère discriminatif du descripteur. ORB utilise directement la méthode gloutonne et la méthode exhaustive pour résoudre ce problème et trouver des paires de points aléatoires avec une faible corrélation.
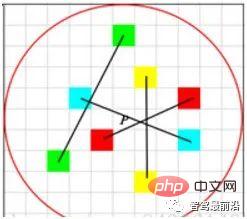
Figure 5 : Mode de sélection des paires de points du descripteur ORB
La méthode d'échantillonnage et la méthode de sélection des paires de points des descripteurs binaires ci-dessus sont conformes à l'intuition générale des gens, tandis que des descripteurs tels que BRISK et FREAK provide Une méthode de construction de modèles binaires plus régulière avec des informations d'échelle intégrées est proposée. Par exemple, le descripteur FREAK imite le modèle d'échantillonnage visuel de l'œil humain. Comme le montre la figure 6, la valeur de chaque point d'échantillonnage est la valeur de gris moyenne dans le cercle rouge et la ligne bleue représente le plan de sélection des paires de points.
Figure 6 : Échantillonnage de descripteurs FREAK, modèle de sélection de paires de points
La haute efficacité des descripteurs binaires se reflète principalement dans trois aspects.
(1) Les descripteurs binaires utilisent des vecteurs binaires comme descriptions de caractéristiques et n'ont besoin que de comparer la taille des paires de points sans calculer de gradients spécifiques.
(2) La comparaison entre deux descripteurs peut utiliser la distance de Hamming (Hamming distance), qui est plus rapide à calculer et plus facile à optimiser.
(3) Puisque chaque vecteur binaire correspond à un nombre décimal, il représente lui-même également un motif, sans qu'il soit nécessaire d'utiliser un histogramme pour le représenter comme SIFT.
Les descripteurs binaires ne sont généralement pas aussi discriminants que les descripteurs de la famille SIFT, mais dans certains scénarios, combinés à une programmation parallèle, l'efficacité peut être des dizaines voire des centaines de fois supérieure tout en garantissant des capacités discriminantes similaires.
3 Création et requête de base de données
La base de données peut être comprise comme l'intégration d'une carte + d'un index. Les cartes peuvent être composées d'images 2D pures, de cartes de nuages de points 3D ou d'une combinaison d'images 2D et de nuages de points 3D. La génération de cartes de nuages de points 3D utilise principalement la méthode de reconstruction tridimensionnelle SfM (Structure from motion) pour déduire des informations 3D à partir d'images 2D de séries chronologiques. Si une caméra binoculaire RVB-D fournit de la profondeur, des informations de points 3D plus précises peuvent être obtenues. Il comprend également certaines stratégies de sélection telles que les images clés. Les méthodes spécifiques dépassent le cadre de cet article. Les étudiants intéressés peuvent vérifier les informations pertinentes par eux-mêmes. Le rôle de la base de données est le suivant :
Pour une image d'observation d'entrée, interrogez l'historique de cartographie (image/nuage de points/points caractéristiques) via la base de données pour obtenir le sous-ensemble de carte (image/nuage de points) qui est le plus susceptible d'être observé dans l'image actuelle/les points caractéristiques), faites correspondre la carte avec les informations d'observation, calculez la matrice de transformation et obtenez la pose de la caméra d'observation.
L'index est la clé pour accélérer ce processus. Les bases de données elles-mêmes ont tendance à être énormes. Prenons l'exemple de l'opération d'essai du robot de poche de Meituan au deuxième étage de Joy City à Chaoyang, Pékin. Trois caméras de profondeur ont été installées. Même après la projection, près de 80 000 images 900 × 600 ont été utilisées. Compte tenu de la nature du positionnement en temps réel, il est impossible de comparer la requête avec 80 000 images une par une à chaque fois. La technologie d'indexation doit donc être utilisée pour accélérer l'ensemble de l'algorithme. Cette technologie recoupe fortement les tests de bouclage en SLAM, la récupération d'images et la reconnaissance de localisation en vision. Seules les méthodes générales sont présentées ci-dessous.
Il y a plusieurs points caractéristiques dans une image. Les points caractéristiques doivent d'abord être codés, comme l'encodage VLAD (Vecteur de descripteurs localement agrégés), et les descripteurs locaux sont utilisés pour former une description globale de l'image. Utilisez ensuite des index, tels que kd-tree, pour effectuer des requêtes au niveau de l'image. Bien entendu, l'encodage et l'indexation peuvent également être effectués en même temps, comme par exemple le modèle hiérarchique du sac de mots (Bag-of-words, BoW) + méthode d'index avant + d'index inverse.
VLAD encoding
VLAD (Vecteur de descripteurs agrégés localement) [10], comme le montre la Fig. 7, est un livre de codes (Codebook) formé en agrégeant des descripteurs locaux, un simple méthode de codage global par cumul de la distance entre le descripteur et le mot de code (Word). Un 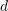 descripteur dimensionnel
descripteur dimensionnel  est codé via le livre de codes de
est codé via le livre de codes de 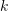 mots de code pour former un
mots de code pour former un 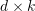 vecteur de description dimensionnelle. La valeur dans le vecteur est le descripteur et le
vecteur de description dimensionnelle. La valeur dans le vecteur est le descripteur et le 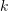 ième mot de code.
ième mot de code. 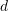 ème dimension. Ensuite, une normalisation
ème dimension. Ensuite, une normalisation 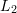 est effectuée pour former le vecteur VLAD final.
est effectuée pour former le vecteur VLAD final.
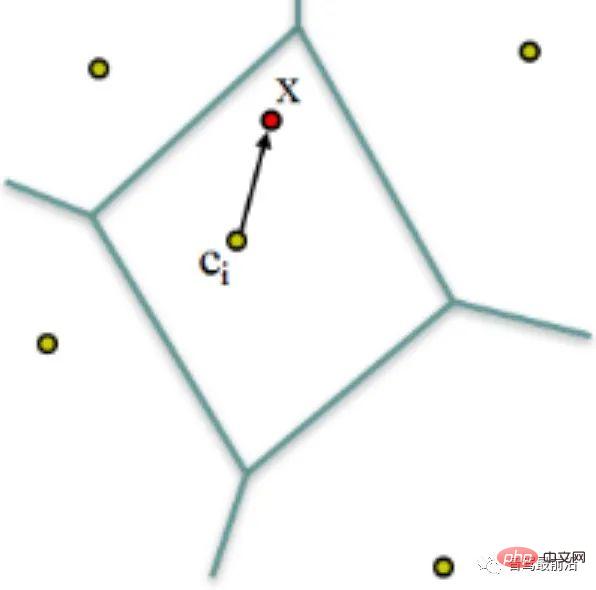
Figure 7 : VLAD encode par la distance entre le descripteur et le mot de code
DenseVLAD[11] et NetVLAD[12] sont spécialement présentés ici. Torii et al., ont prouvé que DenseSIFT surpasse le SIFT standard dans les deux requêtes et correspondances. DenseVLAD extrait les points SIFT à quatre échelles selon un modèle d'échantillonnage en forme de grille d'intervalles de 2 pixels. Échantillonnez aléatoirement 25 millions de descripteurs dans le monde et utilisez l'algorithme k-means pour générer un livre de codes de 128 mots de code. Le vecteur VLAD est réduit dimensionnellement à l'aide de l'ACP (analyse en composantes principales) après normalisation pour former le vecteur DenseVLAD final à 4 096 dimensions. Comme le montre la figure 8, le nombre de points intérieurs (verts) après correspondance à l'aide de DenseSIFT est plus grand.

Figure 8 : Points de fonctionnalité DenseSIFT et SIFT standard, comparaison des points intérieurs (vert) après correspondance
Et NetVLAD ajoute des informations de supervision à VLAD pour améliorer la discriminabilité de l'encodage VLAD. Comme le montre la figure 9, supposons que les deux descripteurs rouge et vert proviennent de deux images qui ne doivent pas correspondre. Puisqu'ils se trouvent tous deux dans un rayon plus grand et à une distance similaire du centre du VLAD (×), après normalisation L2, leurs valeurs codées seront très similaires. Après avoir ajouté les informations de supervision selon lesquelles les images correspondant aux descripteurs rouge et vert ne correspondent pas, le point central (★) généré par NetVLAD peut mieux distinguer les deux descripteurs et augmenter leur différence de distance codée (rayon).
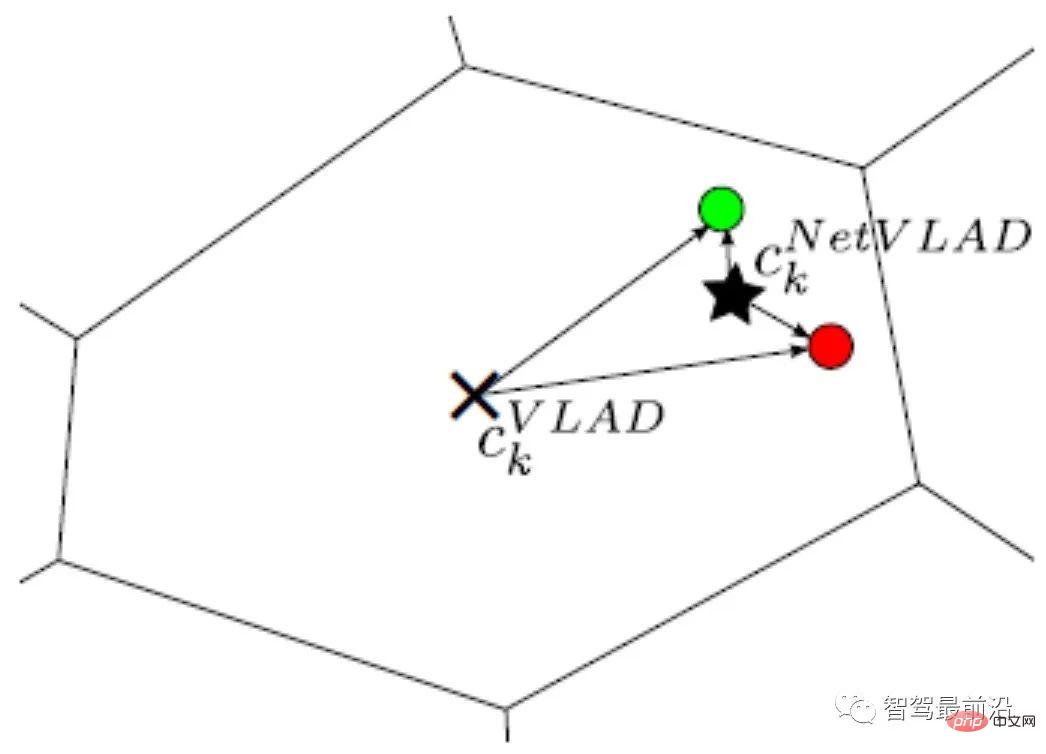
Figure 9 : Comparaison du centre de clustering NetVLAD (×) et du centre de clustering VLAD (★)
Encodage BoW + index
Basé sur un sac de mots Le codage des fonctionnalités et les idées de conception du modèle BoW [13, 14] jouent un rôle décisif dans le développement de la vision par ordinateur et ne seront pas présentés ici. Cet article prend comme exemple une base de données d'images 2D correspondant à des images de requête 2D pour présenter un modèle intégré d'encodage et d'indexation BoW commun. Comme le montre la figure 10, le dictionnaire (vocabulaire) est généré à l'aide d'une méthode hiérarchique pour tous les descripteurs de l'ensemble de données, l'espace est divisé selon une structure arborescente et chaque couche est calculée par regroupement de k-moyennes. Les nœuds feuilles finaux sont équivalents à des mots de code (il y a 9 mots de code sur la figure 10).
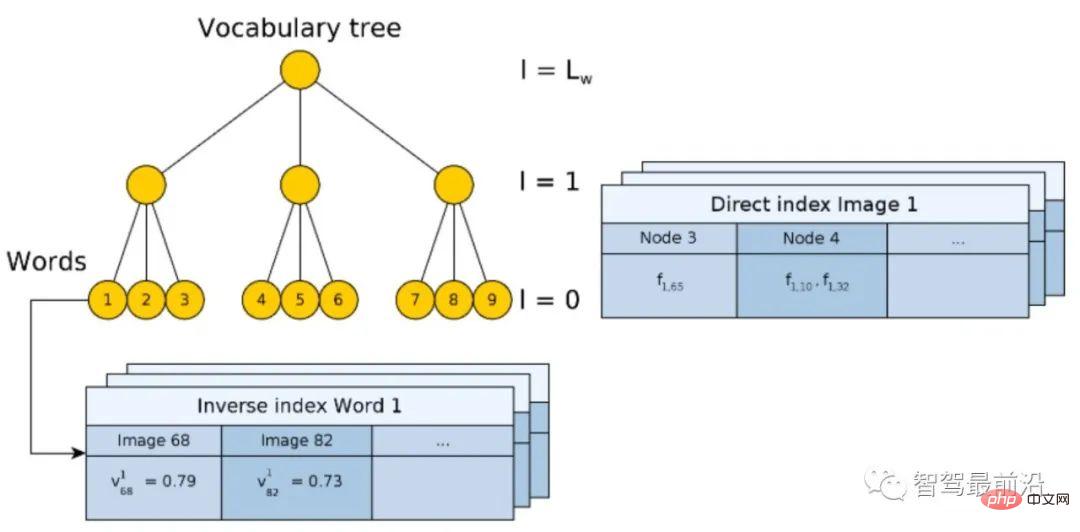
Figure 10 : Modèle BoW hiérarchique avec index direct et index inversé
Le processus de construction de l'arbre est en fait le processus d'encodage de l'image originale. Cependant, l'encodage lui-même n'accélère pas le processus de recherche. Comme pour VLAD, il doit encore être comparé une par une avec les images de la base de données. Par conséquent, un index inverse (Inverse index) est conçu ici, qui ne nécessite pas de comparaison des vecteurs codés. Le principe est illustré sur la figure 11. Pour une image de requête (image de requête), le descripteur extrait est entré dans BoW et finira par tomber dans le nœud feuille du mot de code (mot visuel) k.
Chaque mot de code correspond à un index, enregistrant le poids du mot de code 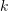 à la
à la  ème image de la base de données
ème image de la base de données 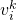 (Fig.10). Ici, le poids est calculé à l'aide de TF-IDF (Fréquence du terme – fréquence du document inverse). Autrement dit, si un mot
(Fig.10). Ici, le poids est calculé à l'aide de TF-IDF (Fréquence du terme – fréquence du document inverse). Autrement dit, si un mot 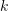 apparaît fréquemment dans une certaine image
apparaît fréquemment dans une certaine image  et a une faible fréquence dans d'autres images, alors ce mot a une meilleure discriminabilité d'image et une valeur de poids plus élevée
et a une faible fréquence dans d'autres images, alors ce mot a une meilleure discriminabilité d'image et une valeur de poids plus élevée 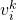 . Enfin, l'image correspondante est sélectionnée via le mécanisme de vote. Il convient également de noter que l'index inversé n'est pas nécessairement construit sur le BoW arborescent, il fournit simplement une méthode de requête rapide.
. Enfin, l'image correspondante est sélectionnée via le mécanisme de vote. Il convient également de noter que l'index inversé n'est pas nécessairement construit sur le BoW arborescent, il fournit simplement une méthode de requête rapide.
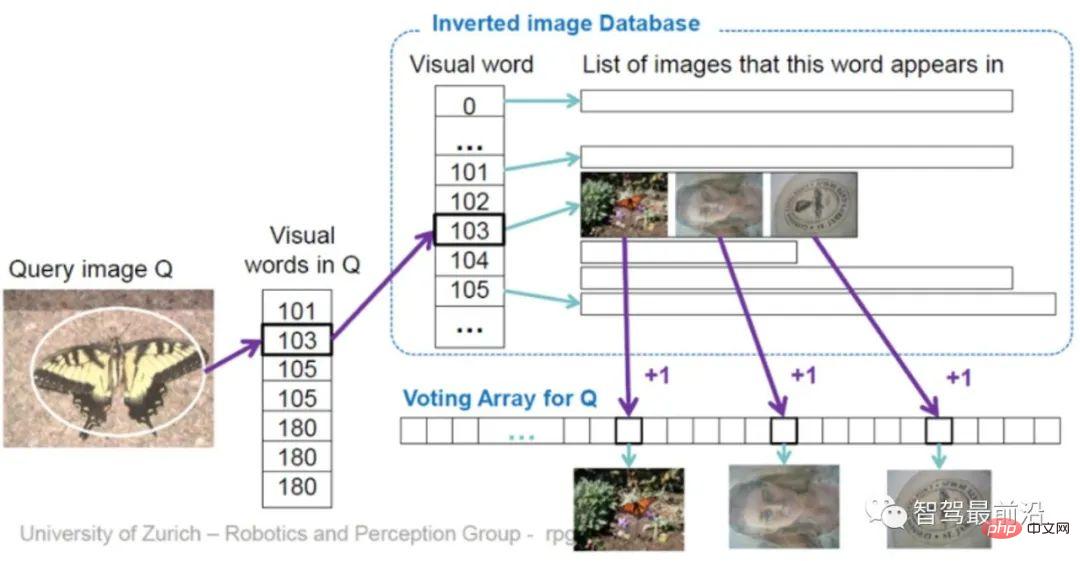
Figure 11 : Grâce au mécanisme d'index inversé + vote, interrogez directement l'image
La fonction de l'index direct (Index Direct) est principalement d'enregistrer les points caractéristiques de l'image de la base de données lorsque construire le BoW. Quels nœuds ont été saisis, de sorte que lorsque l'image est interrogée, il n'est pas nécessaire de calculer les points caractéristiques et que les points caractéristiques peuvent être extraits directement via l'index.
Requête de nuage de points 3D
Dans la requête d'image 2D, l'image est d'abord interrogée à partir du niveau sémantique, de sorte que la plage spatiale des points caractéristiques peut être contrainte à travers l'image. La requête de nuage de points 3D n'a pas de telles contraintes, elle présente donc de nombreuses difficultés. Si vous devez considérer la continuité spatiale, si tous les points interrogés se trouvent dans la plage observable, etc. Nous présentons ici uniquement la méthode publiée par Sattler au TPAMI 2016 [15]. Après des années de peaufinage, ce cadre de méthode est relativement simple et complet. Étant donné que les étapes de recherche de codage par dictionnaire chevauchent le contenu de la section précédente, seuls deux mécanismes, la recherche active et le filtrage de visibilité, sont présentés ici.
La recherche active consiste principalement à rendre les points 3D correspondants aussi proches que possible dans l'espace et à avoir une signification géométrique. Comme le montre la figure 12, le point rouge est mis en correspondance avec un point du nuage de points via une série de processus de codage et de raffinement (ligne rouge). Selon le cadre de priorisation proposé, un point 3D avec la probabilité la plus élevée est trouvé à partir du nuage de points et correspond à l'inverse (ligne bleue) à un point 2D correspondant dans l'image de requête.

Figure 12 : Recherche active
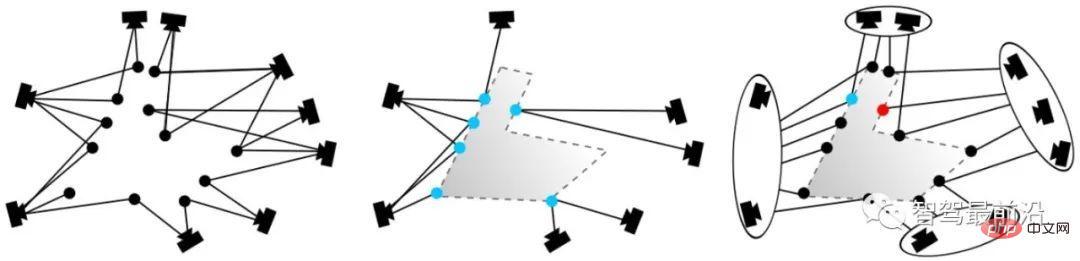
Figure 13 : Filtrage de visibilité
Le filtrage de visibilité consiste principalement à rendre les points correspondants visibles autant que possible à la caméra (le positionnement n'est pas supervisé et il n'est pas possible de savoir si les points correspondants sont corrects). La méthode adoptée ici consiste à créer un graphique de visibilité bipartite lors de l'utilisation de SfM pour créer une carte de nuage de points 3D. Comme le montre la figure 13 (à gauche), lorsqu'un point peut être observé par deux caméras en même temps, une relation topologique est établie. Sur la figure 13 (au milieu), les points bleus correspondent à des points et ils entrent en conflit du point de vue de l'observation. En effectuant un regroupement de graphiques sur la topologie existante, les caméras sont regroupées en deux groupes, comme le montre la figure 13 (à droite). De cette manière, de nouvelles relations topologiques entre graphes peuvent être générées. Ensuite, en évaluant le chevauchement entre chaque sous-graphique, nous filtrons les points les plus susceptibles d'être invisibles.
Il convient de noter que bien que les caméras binoculaires et les caméras RVB-D puissent obtenir de la profondeur, et que l'interrogation d'images 2D puisse également obtenir des coordonnées de points caractéristiques 3D dans une plage limitée, en raison des limitations techniques actuelles, les matériaux intérieurs sont complexes et extérieurs de grande taille. zones Dans les scènes à l'échelle, la profondeur n'est pas fiable. Par conséquent, la mise en correspondance de points d’image 2D et de cartes de nuages de points 3D reste une méthode importante.
4 Correspondance de points caractéristiques
Le processus de correspondance de points caractéristiques peut être complété de manière adaptative dans les requêtes de base de données, ce qui est principalement observé dans les requêtes basées sur des structures 3D. La correspondance peut également être effectuée séparément après la requête, ce qui est plus courant dans les requêtes basées sur des images 2D. Le but de la mise en correspondance de caractéristiques est de fournir des paires de points correspondantes pour les calculs ultérieurs de matrice de transformation afin de réaliser le calcul de pose. L'algorithme de consensus d'échantillon aléatoire (RANSAC) [16] est un algorithme classique de filtrage de données et d'ajustement de paramètres. Il suppose que la distribution des données (inliers) est conforme à un certain modèle mathématique et, grâce à des calculs itératifs, il supprime les valeurs aberrantes et les points de bruit, tout en obtenant les meilleurs paramètres du modèle en termes de probabilité. En positionnement global, les points intérieurs font référence à des correspondances correctes, les points extérieurs font référence à des correspondances incorrectes et le modèle paramétrique fait référence à la matrice de transformation spatiale des paires de points correspondants. Comme le montre la figure 14, après optimisation par l'algorithme RANSAC, la correspondance est plus raisonnable. Le sous-ensemble correspondant que RANSAC s'attend à trouver doit répondre à deux indicateurs : l'erreur de reprojection des points intérieurs est aussi petite que possible ; le nombre de points intérieurs est aussi grand que possible ; Le processus de base est donc le suivant :
① Échantillonnage du sous-ensemble initial. ② Calculez la matrice de transformation.
④ Supprimez les points avec de grosses erreurs
- ⑤ Boucle ①-④ pour conserver la solution correspondante qui répond le mieux à l'index.
- Figure 14 : (En haut) Correspondance des fonctionnalités originales ; (En bas) Correspondance optimisée par l'algorithme RANSAC
- Parmi eux, la correspondance initiale des candidats est générée en fonction de la distance entre les descripteurs. l'erreur de reprojection est uniquement liée à la position spatiale des points clés et n'a rien à voir avec le descripteur lui-même. Veuillez vous référer à « 2.4 Calcul de pose » pour la méthode spécifique de matrice de projection. Il convient de souligner que l'algorithme RANSAC est affecté par l'erreur de correspondance d'origine et la sélection des paramètres. Il ne peut garantir que l'algorithme a une probabilité suffisamment élevée pour être raisonnable, mais n'obtient pas nécessairement le résultat optimal. Les paramètres de l'algorithme incluent principalement le seuil et le nombre d'itérations. La probabilité que RANSAC obtienne un modèle crédible est directement proportionnelle au nombre d'itérations, et le nombre de correspondances obtenues est inversement proportionnel au seuil. Par conséquent, en utilisation réelle, il peut être nécessaire d'essayer à plusieurs reprises différents réglages de paramètres pour obtenir de meilleurs résultats.

Figure 15 : Cadre d'algorithme universel Universal-RANSAC
RANSAC différenciable Étant donné que les descripteurs manuels montrent encore de hautes performances dans le domaine du positionnement, certains chercheurs ont commencé à explorer l'utilisation de l'apprentissage profond pour remplacer certaines parties du cadre algorithmique au lieu d'utiliser directement l'algorithme final. descripteurs de bout en bout. Le modèle d’estimation de pose de bout en bout remplace complètement les méthodes traditionnelles. Le RANSAC différenciable (Differentiable RANSAC, DSAC) [18] vise à remplacer la sélection d'hypothèses déterministes par la sélection d'hypothèses probabilistes, afin que le processus RANSAC puisse être dérivé. Le processus est illustré à la figure 16, dans laquelle l'étape de « notation » utilise toujours la reprojection. erreur En tant qu'indicateur, la différence est que l'erreur est basée sur l'image entière plutôt que sur les points caractéristiques, et le processus original de filtrage de la correspondance des points caractéristiques est remplacé par un processus de filtrage direct de l'hypothèse de pose de la caméra h avec probabilité. Bien que la méthode actuelle présente des limites relativement importantes, la DSAC fournit une idée réalisable sur la manière d’ajouter des connaissances préalables au cadre actuel de l’algorithme de positionnement non supervisé. Figure 16 : Cadre de l'algorithme différentiel RANSAC Pour la paire de points de correspondance correcte qui a été obtenue, la matrice de transformation correspondante (Matrice de transformation) doit être calculée à travers des contraintes géométriques. Puisque les coordonnées du point dans la base de données et la pose de la caméra au moment de l'échantillonnage sont connues, la pose actuelle de la caméra peut être obtenue en faisant correspondre la matrice de transformation du point au point de la carte. Certains symboles de base sont définis ici. Les paramètres internes de la caméra sont où, est la matrice de rotation, et est la matrice de translation. 2.4.1 Calcul de matrice de transformation 2D-2D Figure 17 : Géométrie épipolaire dans le calcul de matrice de transformation 2D-2D Pour les deux images 2D correspondantes Paire de points caractéristiques (), leurs coordonnées sur le plan normalisé sont (), et la matrice de transformation correspondante doit être calculée via des contraintes épipolaires. Comme le montre la figure 17, sa signification géométrique est que les trois sont coplanaires. Cette surface est également appelée le plan polaire, Parmi eux, Puisque la matrice essentielle Calcul de matrice de transformation 2D-3D La correspondance 2D-3D est une méthode importante dans l'estimation de pose. Généralement, la méthode PnP est utilisée, c'est-à-dire que les points de correspondance 2D-3D sont connus et que la matrice de transformation est résolue pour obtenir la pose de la caméra. Nous projetons le point 3D P(X, Y, Z) sur le plan d'imagerie de la caméra ( Parmi eux, De cette façon, au moins 6 paires de points correspondants peuvent être résolues, et lorsque le nombre de correspond est supérieur à 6, il peut être utilisé. Des méthodes telles que SVD sont résolues en construisant les moindres carrés. La méthode P3P peut être considérée comme une solution spéciale de la méthode PnP. Comme le montre la figure 18, elle utilise les propriétés de similarité des triangles pour ajouter plus de contraintes et n'a besoin que de 3 paires de points pour résoudre le problème. D'autres méthodes de solution incluent la transformation linéaire directe (DLT), la méthode EPnP (Efficient PnP) et UPnP (Uncalibrated PnP), etc. Par rapport aux méthodes d'optimisation linéaire ci-dessus, les méthodes d'optimisation non linéaires telles que l'ajustement de faisceau (BA) sont également largement utilisées. La méthode BA est une sorte de « taille unique » dans le SLAM visuel. Elle peut optimiser plusieurs variables en même temps, ce qui peut atténuer dans une certaine mesure l'instabilité du système causée par les erreurs locales. informations pertinentes pour une compréhension plus approfondie. Figure 18 : Méthode P3P dans le calcul de matrice de transformation 2D-3D Calcul de matrice de transformation 3D-3D Matrice de transformation entre points 3D Cela peut être résolu à l’aide de l’algorithme itératif du point de placard (ICP). En supposant que le résultat de la correspondance des paires de points ( ou utiliser la méthode d'optimisation non linéaire Bundle Adjustment basée sur l'algèbre de Lie pour résoudre où, Il a été prouvé que le problème ICP a une solution unique et des solutions infinies. Par conséquent, lorsqu'il existe une solution unique, la fonction d'optimisation est équivalente à une fonction convexe et la valeur minimale est la solution optimale globale. Quel que soit le type d'initialisation adopté, cette solution unique peut être obtenue. C’est l’un des grands avantages de la méthode ICP. Cet article présente l'algorithme d'estimation de pose basé sur des points caractéristiques sous quatre aspects : description de l'image, requête de mappage, correspondance de caractéristiques et calcul de pose. Bien que la méthode traditionnelle de positionnement visuel global reste le premier choix dans les applications pratiques, la méthode traditionnelle repose sur le principe selon lequel les points caractéristiques sont correctement définis, correctement extraits, correctement mis en correspondance et correctement observés. Ce principe est très important pour la vision. en soi. C'est un énorme défi. Deuxièmement, étant donné que la méthode traditionnelle est un cadre en plusieurs étapes plutôt que de bout en bout, chaque lien et l'interaction entre les liens nécessitent de nombreux ajustements de paramètres, et la technologie de chaque lien peut être utilisée comme une direction de recherche distincte. Dans l'application réelle, un grand nombre d'astuces correspondant à des scénarios spécifiques doivent être ajoutées, ce qui rend l'ingénierie plus complexe. Et les attentes des gens pour la méthode de bout en bout ont donné naissance à des réseaux tels que PoseNet, VLocNet, HourglassNet, etc., qui ont obtenu de bons résultats sur les benchmarks. L'auteur estime qu'il existe encore de nombreux problèmes dans la méthode de bout en bout actuelle. Les principaux sont que la fonction de perte manque de contraintes géométriques, que l'espace de pose à 6 degrés de liberté lors de la construction de la carte n'est pas continu, et il est difficile de former une bonne cartographie avec l'espace d'entrée, et il y a un manque de régression de posture correspondante, de mécanisme de raffinement, etc. On ne peut nier qu’en tant qu’outil de modélisation le plus puissant pour l’espace non linéaire, l’apprentissage profond apparaîtra davantage dans le domaine du positionnement à l’avenir. Retour au positionnement visuel lui-même, car les avantages les plus importants de la vision sont son faible coût, sa sémantique riche et le peu de restrictions sur les scénarios d'utilisation. Par conséquent, le positionnement de solutions de fusion axées sur la vision et complétées par d’autres capteurs à faible coût constituera également un sujet important à l’avenir. 
5 Calcul de pose
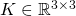 , et la forme homogène du moment de transformation
, et la forme homogène du moment de transformation 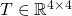 est :
est : 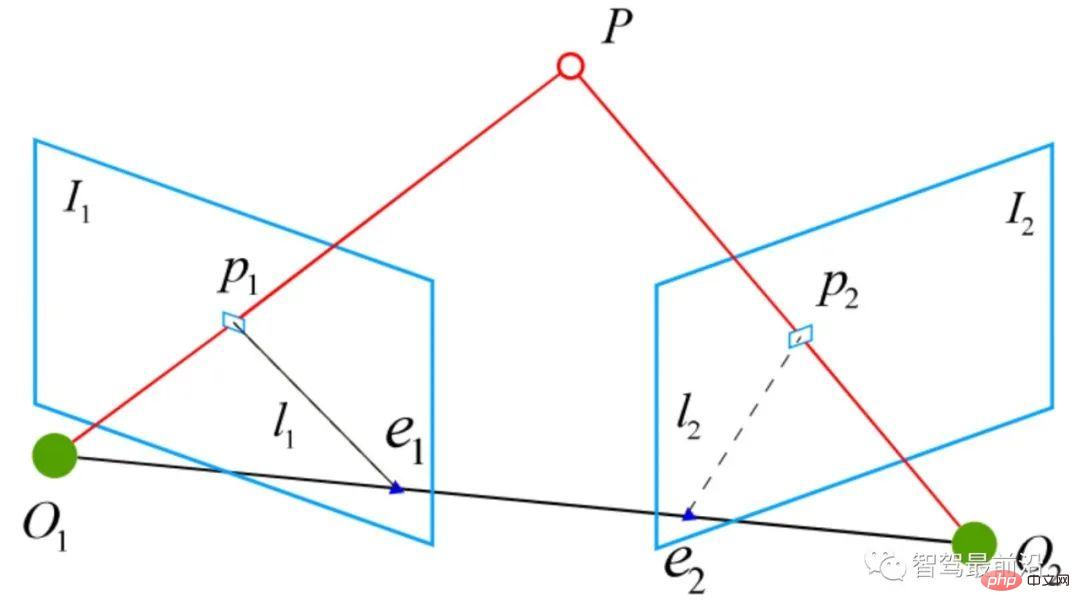
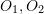 est appelée la ligne de base et
est appelée la ligne de base et 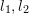 est appelée la ligne polaire. La contrainte épipolaire inclut à la fois la translation et la rotation, qui est définie comme :
est appelée la ligne polaire. La contrainte épipolaire inclut à la fois la translation et la rotation, qui est définie comme : 
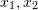 est la coordonnée de
est la coordonnée de 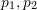 sur le plan normalisé, et ∧ est l'opérateur du produit externe. En comptant la partie médiane de la formule comme matrice de base
sur le plan normalisé, et ∧ est l'opérateur du produit externe. En comptant la partie médiane de la formule comme matrice de base 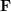 et matrice essentielle
et matrice essentielle 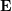 , nous avons :
, nous avons : 
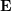 n'a pas d'information d'échelle, donc E est multiplié par toute constante non nulle pour obtenir la polarité. Les contraintes sont toujours valables.
n'a pas d'information d'échelle, donc E est multiplié par toute constante non nulle pour obtenir la polarité. Les contraintes sont toujours valables. 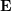 peut être résolu par l'algorithme classique en 8 points (algorithme à huit points), puis décomposé pour obtenir
peut être résolu par l'algorithme classique en 8 points (algorithme à huit points), puis décomposé pour obtenir 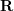 ,
, 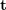 . Par conséquent, on peut voir que la méthode de solution matricielle de transformation 2D-2D présente deux inconvénients. Premièrement, la vision monoculaire présente une incertitude d'échelle et les informations d'échelle doivent être fournies par
. Par conséquent, on peut voir que la méthode de solution matricielle de transformation 2D-2D présente deux inconvénients. Premièrement, la vision monoculaire présente une incertitude d'échelle et les informations d'échelle doivent être fournies par 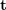 lors de l'initialisation. En conséquence, l'initialisation monoculaire ne peut pas seulement être une pure rotation, mais doit avoir un degré de translation suffisant, sinon cela fera que
lors de l'initialisation. En conséquence, l'initialisation monoculaire ne peut pas seulement être une pure rotation, mais doit avoir un degré de translation suffisant, sinon cela fera que 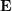 sera nul.
sera nul.  ) :
) : 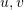
 se trouve la balance,
se trouve la balance, 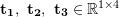 . La solution de cette équation peut être réduite à un problème d'équation linéaire, et chaque caractéristique peut fournir deux contraintes linéaires :
. La solution de cette équation peut être réduite à un problème d'équation linéaire, et chaque caractéristique peut fournir deux contraintes linéaires : 
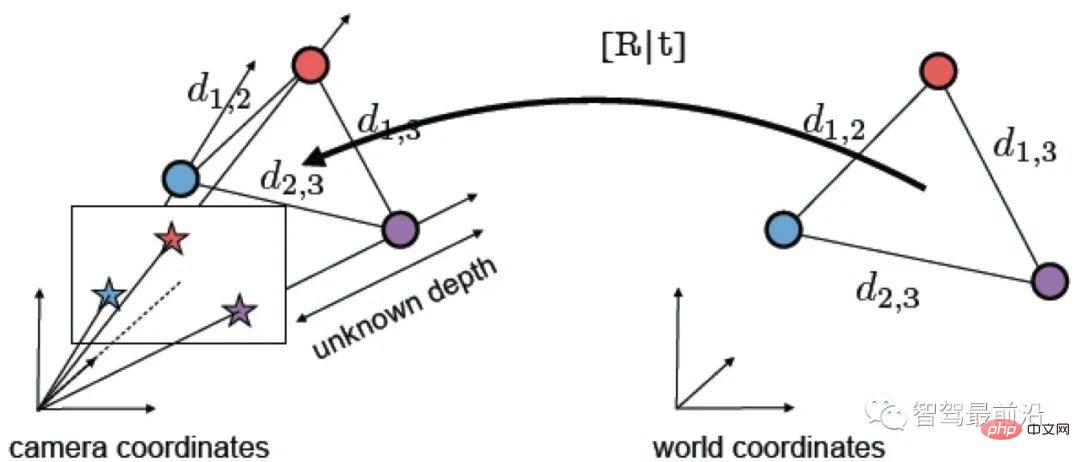
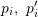 ) est correct, la matrice de transformation obtenue devrait minimiser l'erreur de reprojection
) est correct, la matrice de transformation obtenue devrait minimiser l'erreur de reprojection 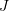 . Vous pouvez utiliser SVD pour résoudre le problème des moindres carrés :
. Vous pouvez utiliser SVD pour résoudre le problème des moindres carrés : 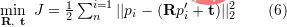
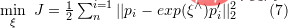
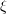 représente la pose de la caméra. L'objectif d'optimisation ici est similaire à celui de l'ajustement du bundle dans la correspondance 2D-3D, mais il n'est pas nécessaire de prendre en compte les paramètres internes de la caméra
représente la pose de la caméra. L'objectif d'optimisation ici est similaire à celui de l'ajustement du bundle dans la correspondance 2D-3D, mais il n'est pas nécessaire de prendre en compte les paramètres internes de la caméra 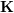 car les points 2D sur l'image originale ont été déplacés du plan d'imagerie de la caméra à travers les jumelles. caméra ou caméra de profondeur RVB-D Projetée dans un monde 3D.
car les points 2D sur l'image originale ont été déplacés du plan d'imagerie de la caméra à travers les jumelles. caméra ou caméra de profondeur RVB-D Projetée dans un monde 3D.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

