Analyse complète des grands paramètres du modèle et réglage fin efficace, recherche Tsinghua publiée dans la sous-journal Nature

Ces dernières années, l'équipe de Sun Maosong du Département d'informatique de l'Université Tsinghua a exploré en profondeur le mécanisme et les caractéristiques des méthodes de réglage efficaces pour les grands paramètres du modèle de langage, et a collaboré avec d'autres équipes compétentes de l'école pour compléter le Le résultat de la recherche "Efficient fine-tuning of settings for large-scale pre-trained Language models" (Parameter -efficient Fine-tuning of Large-scale Pre-trained Language Models) a été publié dans "Nature Machine Intelligence" le 2 mars. Les résultats de la recherche ont été réalisés conjointement par des enseignants et des étudiants du Département d'informatique tels que Sun Maosong, Li Juanzi, Tang Jie, Liu Yang, Chen Jianfei, Liu Zhiyuan et la Shenzhen International Graduate School Zheng Liu Zhiyuan, Zheng Haitao, et Sun Maosong sont les auteurs correspondants de l'article et sont titulaires d'un doctorat au Département d'informatique de l'Université Tsinghua. Sheng Dingning (mentor Zheng Haitao) et Qin Yujia (mentor Liu Zhiyuan) sont les co-premiers auteurs de cet article.

Contexte et aperçu

Depuis 2018, le modèle linguistique pré-entraîné (PLM) et sa méthode de « réglage fin de pré-entraînement » sont devenus le paradigme principal pour les tâches de traitement du langage naturel (NLP), qui utilise d'abord de grandes mettre à l'échelle des données non étiquetées Pré-entraîner un grand modèle de langage grâce à un apprentissage auto-supervisé pour obtenir un modèle de base, puis utiliser les données annotées des tâches en aval pour effectuer un apprentissage supervisé afin d'affiner les paramètres du modèle afin de parvenir à une adaptation aux tâches en aval.

Avec le développement de la technologie, le PLM est sans aucun doute devenu l'infrastructure pour diverses tâches de PNL, et dans le développement du PLM, il existe une tendance apparemment irréversible : la taille du modèle devient de plus en plus grande. Des modèles plus grands obtiendront non seulement de meilleurs résultats sur des tâches connues, mais montreront également le potentiel d’accomplir des tâches inconnues plus complexes.

Cependant, les modèles plus grands sont également confrontés à de plus grands défis d'application. La méthode traditionnelle de réglage précis des paramètres de modèles pré-entraînés à très grande échelle consommera une grande quantité de ressources de calcul et de stockage GPU, ce qui entraînera d'énormes coûts. les coûts. C’est intimidant. Ce coût a également créé une sorte d'« inertie » dans le monde académique, c'est-à-dire que les chercheurs vérifient leurs méthodes uniquement sur des modèles à petite et moyenne échelle et ignorent généralement les modèles à grande échelle.

Dans les statistiques de cet article, nous avons sélectionné au hasard 1 000 articles des cinq dernières conférences PNL et avons constaté que l'utilisation de modèles pré-entraînés est devenue un paradigme de recherche fondamentale, mais qu'il y en a très peu qui impliquent de grands modèles (Figure 1 illustrée) .

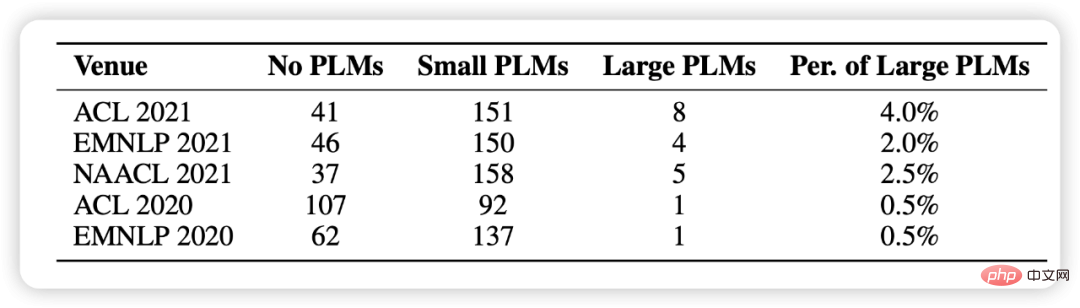
Figure 1 : Répartition statistique des modèles pré-entraînés utilisés dans 1000 articles sélectionnés au hasard

Dans ce contexte, un nouveau schéma d'adaptation de modèle, Méthodes efficaces en termes de paramètres sont Attirant progressivement l'attention. Par rapport au réglage fin standard de tous les paramètres, ces méthodes n'affinent qu'une petite partie des paramètres du modèle tout en laissant le reste inchangé, réduisant ainsi considérablement les coûts de calcul et de stockage. réglage fin des paramètres complets. Nous pensons que ces méthodes s'ajustent essentiellement sur un « incrément » (Delta Paremters), c'est pourquoi nous l'avons nommé Delta Tuning.

Dans cet article, nous définissons et décrivons le problème du Delta Tuning, et passons en revue les recherches antérieures à travers un cadre unifié. Dans ce cadre, les méthodes de réglage delta existantes peuvent être divisées en trois groupes : les méthodes incrémentielles (basées sur les ajouts), basées sur les spécifications (basées sur les spécifications) et les méthodes de reparamétrage (reparamétrisation).

En plus de sa signification pratique, nous pensons qu'il a également une signification théorique très importante. Delta Tuning révèle dans une certaine mesure le mécanisme derrière les grands modèles et nous aide à développer davantage de méthodes pour les grands modèles et même la théorie des réseaux de neurones profonds. À cette fin, nous proposons un cadre théorique pour discuter du Delta Tuning sous les deux perspectives de optimisation et contrôle optimal afin de guider la conception ultérieure de la structure et de l'algorithme. De plus, nous effectuons une comparaison expérimentale complète de méthodes représentatives et démontrons une comparaison complète des performances de différentes méthodes sur les résultats de plus de 100 tâches de PNL. Les résultats expérimentaux couvrent la recherche et l'analyse des performances de Delta Tuning, des performances de convergence, des performances d'efficacité, de la puissance d'échelle, des performances de généralisation et des performances de migration. Nous avons également développé OpenDelta, une boîte à outils open source qui permet aux praticiens de mettre en œuvre Delta Tuning sur PLM de manière efficace et flexible.

• Lien papier : https://www.nature.com/articles/s42256-023-00626-4
• Boîte à outils OpenDelta : https://github.com/thunlp/OpenDelta

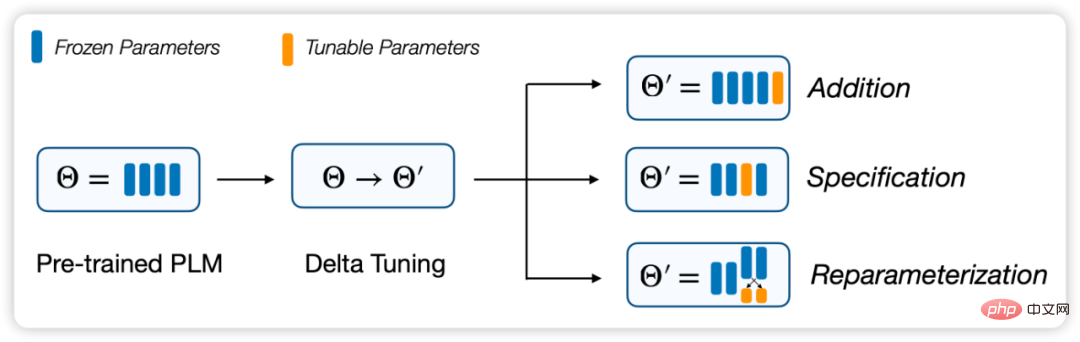
Figure 2 : Cadre de division de Delta Tuning

Delta Tuning : méthode et analyse

Étant donné un modèle pré-entraîné et des données d'entraînement, l'objectif de l'adaptation PLM est de générer un modèle. les paramètres sont. sera défini comme une opération au-dessus du modèle original. Pour le réglage traditionnel des paramètres complets, il existe

, où

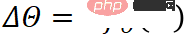
est la valeur mise à jour de tous les paramètres dans

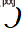
par rapport aux données d'entraînement. Dans Delta Tuning,

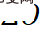
fait référence à la modification d'un petit nombre de paramètres. Empiriquement parlant, le réglage fin de tous les paramètres a

, tandis que Delta Tuning a

. Par conséquent, nous pouvons diviser le Delta Tuning efficace en termes de paramètres en trois stratégies basées sur la forme et la structure des paramètres ajustés, et trier les méthodes précédentes :

Méthode basée sur les additions

Ces méthodes de classe introduisent des modules neuronaux supplémentaires pouvant être entraînés ou paramètres qui ne sont pas présents dans le modèle original. Dans ce type de méthode, sur la base de la définition ci-dessus, nous avons

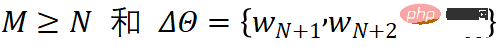
. Les méthodes incrémentielles courantes incluent le réglage de l'adaptateur, le réglage du préfixe, le réglage des invites, etc. Ils insèrent invariablement des modules neuronaux à petite échelle ou des paramètres réglables dans le modèle et réalisent une adaptation efficace du modèle en ajustant uniquement cette petite partie des paramètres. Parmi eux, le réglage de l'adaptateur est le travail pionnier de ce type de méthode. Il prouve que le simple ajout d'un simple réseau neuronal à chaque couche peut être comparable à un réglage fin de paramètres complets sur de nombreuses tâches. Dans le même temps, Adapter démontre également son potentiel dans des scénarios multitâches et multilingues. Le réglage des préfixes et le réglage des invites sont des algorithmes de réglage delta très populaires récemment. Ils insèrent des vecteurs réglables dans la couche d'entrée ou la couche de présentation pour un réglage précis. Parmi eux, Prompt Tuning peut être considéré comme une version simplifiée de Prefix Tuning, c'est-à-dire qu'il ajoute uniquement Soft Prompt à la couche d'entrée. Cette approche présente un très gros avantage, c'est-à-dire qu'il n'est pas nécessaire de modifier la structure interne du modèle. En même temps, à mesure que le nombre de paramètres du modèle augmente jusqu'à 10 milliards, il a également été prouvé qu'elle peut atteindre cet objectif. même effet que le réglage fin des paramètres complets sur certaines données. Cependant, ce type de méthode est également confronté à d’importants problèmes d’optimisation. Des expériences ont prouvé que son efficacité d’optimisation est souvent inférieure à celle d’autres paradigmes de réglage fin, que son temps de convergence est plus long et qu’elle fonctionne mal sur des modèles de petite et moyenne taille.

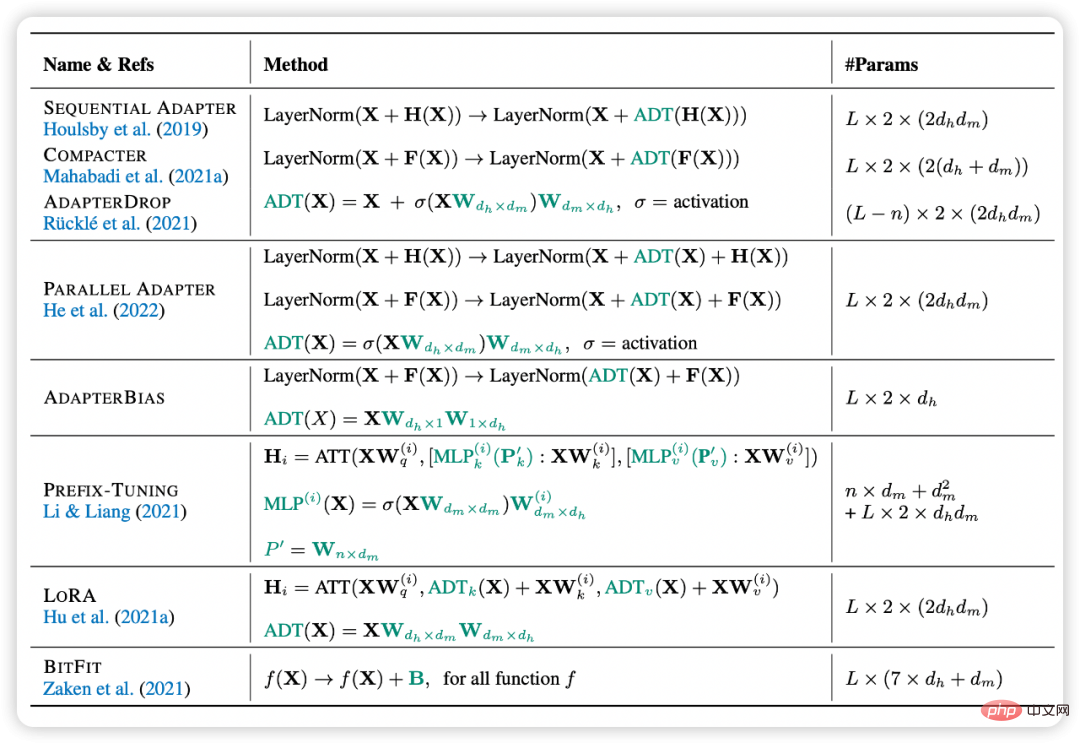
Figure 3 : Expression formelle du réglage Delta

Méthode basée sur les spécifications

Ce type de méthode spécifie que certains paramètres du modèle d'origine deviennent entraînables, tandis que d'autres paramètres sont gelés. Dans ce type de méthode, nous pouvons représenter le paramètre d'entraînement défini par , et les paramètres mis à jour à ce moment-là par . puis la valeur incrémentale, sinon. La méthode spécifiée n'introduit aucun nouveau paramètre dans le modèle, ni ne cherche à modifier la structure du modèle, mais spécifie directement certains paramètres à optimiser. L'idée est simple mais fonctionne étonnamment bien, par exemple certaines méthodes n'affinent qu'un quart de la dernière couche de BERT et RoBERTa et peuvent produire 90 % des performances d'un réglage fin complet des paramètres. Un travail de BitFit montre qu'en optimisant uniquement les termes de biais à l'intérieur du modèle et en gelant d'autres paramètres, le modèle peut toujours reproduire plus de 95 % des performances de réglage fin de tous les paramètres sur plusieurs benchmarks. Les résultats empiriques de BitFit montrent également que même si nous utilisons un petit jeu de paramètres aléatoires pour le réglage delta (ce qui dégrade évidemment les performances), le modèle peut toujours produire des résultats acceptables sur le benchmark GLUE. Une autre observation intéressante est que différents termes de biais peuvent avoir des fonctions différentes lors de l'adaptation du modèle.

En plus de spécifier manuellement ou heuristiquement les paramètres à mettre à jour, nous pouvons également apprendre une telle spécification. Diff Pruning est l'un des travaux représentatifs, qui reparamétre les paramètres du modèle affinés en la somme de paramètres pré-entraînés et d'un vecteur de différence, c'est-à-dire. La question clé à l'heure actuelle est d'encourager le vecteur de différence à être aussi clairsemé que possible. Ce travail régularise le vecteur par approximation différentiable pour atteindre l'objectif de parcimonie. En fait, le Diff Pruning consomme plus de mémoire GPU que le réglage fin de tous les paramètres en raison de l'introduction de nouveaux paramètres à optimiser pendant la phase d'apprentissage, ce qui peut s'avérer difficile dans les applications sur de gros PLM. La méthode de masquage (Masking) apprend un masque sélectif pour le PLM, mettant à jour uniquement les poids critiques pour une tâche spécifique. Pour apprendre un tel ensemble de masques, une matrice binaire liée aux poids du modèle est introduite, où chaque valeur est générée par une fonction de seuil. Lors de la rétropropagation, la matrice est mise à jour par l'estimateur de bruit.

Méthode basée sur le reparamétrage

Ce type de méthode reparamétre le processus d'optimisation existant en une forme valide en paramètres en le transformant. Désignons l'ensemble de paramètres à reparamétrer par , et en supposant que chacun est représenté par de nouveaux paramètres, alors les paramètres mis à jour sont notés par , où . En termes simples, les méthodes de reparamétrage sont souvent basées sur une hypothèse similaire : que le processus d'adaptation du modèle pré-entraîné est intrinsèquement de bas rang ou de faible dimension. Ce processus peut donc être équivalent à un paradigme efficace en termes de paramètres.

Par exemple, nous pouvons supposer que l'adaptation du modèle a une « dimension intrinsèque ». En reparamétrant le processus de réglage fin en un processus d'optimisation d'un sous-espace de faible dimension, nous pouvons obtenir des résultats impressionnants simplement en affinant. les paramètres dans le sous-espace. Performance satisfaisante. En ce sens, le PLM peut servir de cadre de compression universel pour compresser la complexité de l’optimisation des dimensions élevées aux dimensions faibles. En général, les PLM plus grands ont généralement des dimensions intrinsèques plus petites, et le processus de pré-formation réduit implicitement les dimensions intrinsèques du PLM. Inspirée par ces observations, la méthode reparamétrée Delta Tuning a également été proposée, qui reparamétre (une partie des) paramètres du modèle d'origine à l'aide de paramètres de substitution de faible dimension, optimisant uniquement les paramètres de substitution, réduisant ainsi les coûts de calcul et de mémoire.

Un autre ouvrage bien connu, LoRA, suppose que les changements de poids lors de l'ajustement du modèle ont un « rang intrinsèque » faible. Sur la base de cette hypothèse, ils proposent d'optimiser la décomposition de bas rang pour les changements dans la matrice de poids d'origine dans le module d'auto-attention. Lors du déploiement, les matrices de décomposition de bas rang optimisées sont multipliées pour obtenir l'incrément de la matrice de poids d'auto-attention. De cette façon, LoRA peut égaler les performances affinées du benchmark GLUE. Ils démontrent l’efficacité de leur approche sur des PLM de différentes tailles et architectures, même GPT3.

Ces hypothèses de faible dimension conviennent non seulement à l'adaptation d'une seule tâche, mais peuvent également être étendues à des scénarios multitâches. IPT suppose que le même sous-espace propre de faible dimension existe pour plusieurs tâches, et le simple ajustement des paramètres du sous-espace peut obtenir des résultats satisfaisants sur plus de 100 tâches PNL en même temps. Au lieu d'utiliser des sous-espaces aléatoires, cette méthode tente de trouver un sous-espace commun partagé par plusieurs tâches NLP. Les expériences montrent que dans un sous-espace de basse dimension de 250 dimensions, plus de 80 % des performances du Prompt Tuning peuvent être reproduites sur plus de 100 tâches PNL en ajustant seulement 250 paramètres.

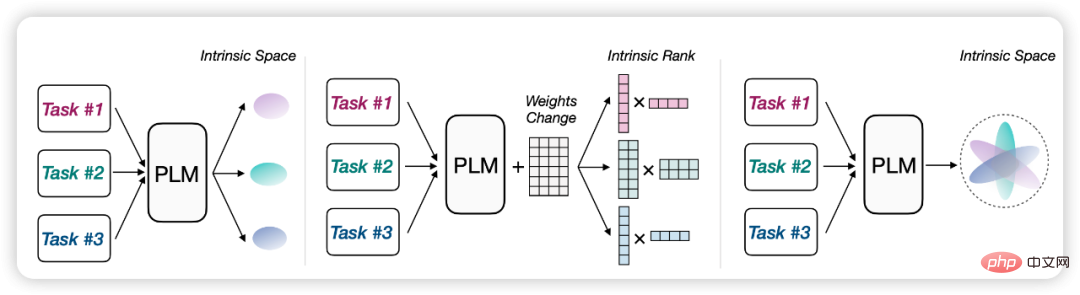
Figure : Les méthodes de reparamétrage sont souvent basées sur des hypothèses similaires de faible dimension ou de faible rang

Perspective théorique du réglage Delta

Le réglage Delta a-t-il quelque chose de essentiellement en commun ? Nous pensons que la méthode Delta Tuning a non seulement une grande valeur pratique, mais a également une signification théorique de grande envergure. Elles semblent toutes prouver invariablement une chose : c'est-à-dire que le processus d'adaptation de grands modèles semble être un processus très peu coûteux. (par rapport à (pour la pré-formation), cela peut être fait avec très peu de données et très peu de réglages de paramètres. Le succès de Delta Tuning nous a inspiré à explorer davantage le cadre théorique derrière l'adaptation du modèle. Cet article propose un cadre sous deux perspectives : optimisation et contrôle optimal pour expliquer Delta Tuning à un niveau théorique.

Angle d'optimisation

Delta Tuning tente d'obtenir l'effet d'un réglage fin de tous les paramètres sur le modèle de langage original à grande échelle en ajustant avec précision un petit nombre de paramètres et en réduisant l'utilisation de la mémoire. Du point de vue de l'optimisation, nous analysons l'effet du Delta Tuning et discutons de la conception de certaines méthodes de Delta Tuning sous des hypothèses de faible dimension. Après avoir utilisé Delta Tuning, la fonction objectif et les paramètres dont elle dépend peuvent changer. Pour la nouvelle fonction objectif, seuls les paramètres liés au Delta Tuning sont optimisés. Si la valeur initiale est suffisamment bonne, les performances du modèle ne seront pas significativement endommagées sous certaines hypothèses. Mais afin de garantir l’efficacité du Delta Tuning, il est nécessaire de développer la structure du problème pour concevoir cette nouvelle fonction objectif. Le point de départ est d’exploiter la nature inhérente du problème à faible dimension. De manière générale, deux idées se sont avérées utiles dans la pratique :

• Trouver des vecteurs de solution dans un sous-espace spécifique de faible dimension ;
• Approximer la cible dans une fonction spécifique de l'espace de fonctions de faible dimension.

Parce que pour la plupart des applications en apprentissage profond, la fonction objectif a généralement de nombreux points minimum locaux, donc lorsque la valeur initiale est proche d'un point minimum local, seules les directions de recherche individuelles sont importantes, ou la fonction objectif est dans Ceci le voisinage peut être approximé par des fonctions plus simples. Par conséquent, les deux idées d’optimisation devraient donner de bons résultats, et l’optimisation des paramètres de faible dimension est généralement plus efficace et plus stable.

Une représentation en basse dimension de l'espace de solution. La recherche a montré que l'optimisation des paramètres des modèles de langage pré-entraînés suit une variété de basse dimension (Aghajanyan et al., 2021), de sorte que cette variété peut être intégrée dans une représentation de basse dimension du vecteur de solution. Si cette représentation de faible dimension est exacte, alors le réglage fin de tous les paramètres sur le modèle d'origine équivaut à un réglage fin sur ce paramètre de faible dimension. S'il y a une erreur dans la représentation de basse dimension, alors lorsque la fonction objectif du modèle pré-entraîné et la nouvelle fonction objectif satisfont à la continuité Lipschitzienne, la différence d'effet final entre le réglage fin des paramètres complets et la précision des paramètres de basse dimension - le réglage est également contrôlable.

Certaines méthodes de Delta Tuning bénéficient de cette idée de conception. Par exemple, dans LoRA (Hu et al., 2021a), la matrice de poids adopte une approximation de bas rang ; dans BitFit (Zaken et al., 2021) et l'élagage différentiel (Guo et al., 2021), seuls certains paramètres sélectionnés sont optimisation. L’essence de ces méthodes est de mettre à jour les paramètres dans un sous-espace plus petit du vecteur solution et d’obtenir finalement de meilleurs résultats.

représentation en basse dimension de l'espace fonctionnel. Une autre approche consiste à concevoir directement une fonction d'approximation de la fonction objectif d'origine et à s'attendre à ce que l'erreur approximative de cette fonction soit faible. De telles approximations de fonctions peuvent être des réseaux incrémentaux (Houlsby et al., 2019) ou des espaces de fonctionnalités augmentés (Lester et al., 2021). Parce que nous sommes généralement plus préoccupés par l’effet final du modèle de langage, il est raisonnable de considérer directement l’effet approximatif sur la fonction objectif elle-même.

Il existe de nombreuses façons différentes de construire de telles approximations de fonctions dans la pratique. Le plus simple consiste à fixer certains paramètres du réseau et à affiner uniquement le reste. Cette méthode suppose qu'une partie du réseau reflète approximativement les performances de l'ensemble du réseau. Étant donné que le rôle des fonctions dans le réseau est caractérisé par le flux de données, des représentations de bas rang peuvent être injectées dans le chemin de données du réseau d'origine, et le nouveau modèle qui en résulte est un réseau incrémentiel, tel qu'un adaptateur. L'erreur de la fonction est déterminée par le pouvoir de représentation du réseau delta.

Si la structure autorégressive de Transformer est développée, des approximations de fonctions plus raffinées peuvent également être obtenues. Par exemple, le réglage des invites (Lester et al., 2021) ajoute une série de jetons d'invite comme préfixes à l'entrée et ajuste uniquement les paramètres dont dépendent ces jetons d'invite. Cette méthode peut être considérée comme une augmentation de l'espace des fonctionnalités, et grâce aux propriétés de Transformer, une telle fonction peut mieux se rapprocher de la fonction d'origine et guider le modèle de langage pour se concentrer sur des tâches spécifiques. Les méthodes associées incluent le réglage des préfixes (Li & Liang, 2021). Des expériences ont montré que le réglage rapide présente de meilleurs avantages pour les modèles plus grands et les ensembles de données plus volumineux, car ces méthodes utilisent essentiellement des fonctions de faible dimension pour approximer des fonctions de grande dimension lorsque l'échelle du modèle et des données augmente. grand, il y a naturellement plus de degrés de liberté pour choisir le sous-espace d’approximation des fonctions.

Deux représentations de basse dimension peuvent généralement conduire à des méthodes de réglage Delta formellement similaires. (He et al., 2022) ont fait une déclaration formellement unifiée sur l'adaptateur, le réglage des préfixes et LoRA, qui peut être considérée comme une vision de diverses techniques de réglage Delta du point de vue de l'approximation des fonctions. Notre discussion montre que ces méthodes de réglage delta reposent sur des hypothèses de faible dimension. En fait, il existe même des sous-espaces communs de faible dimension pour différentes tâches (Qin et al., 2021b). Su et al. (2021) et notre section expérimentale démontrent également la transférabilité du Delta Tuning entre différentes tâches. Étant donné que l'effet réel du Delta Tuning est inévitablement lié à la tâche, afin d'obtenir l'effet d'un réglage fin de tous les paramètres, il est avantageux de mieux explorer et utiliser la structure du problème lui-même ou de concevoir des algorithmes hybrides.

Angle de contrôle optimal

Sur la base de théories précédentes expliquant l'apprentissage profond du point de vue du contrôle optimal, nous avons révélé que le Delta Tuning peut être considéré comme un processus de recherche du contrôleur optimal. Pour un modèle de classification autorégressive, le modèle générera des prédictions d'étiquettes dans la dernière étape (étiquetée comme position). Ce processus d'optimisation peut être exprimé comme suit :

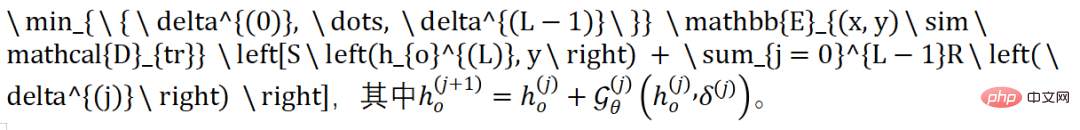
La fonction définit ici le Delta dans la propagation avant PLM de. changements sous intervention. Plus précisément, les activations apprenables proviennent des paramètres fixes de afin que la représentation au niveau de la couche puisse être correctement transformée en . Par conséquent, la transformation de représentation entre deux couches consécutives est décrite par la fonction et la connexion résiduelle dans Transformer. Qu'il s'agisse de la méthode basée sur l'addition d'adaptateur et de préfixe, de la méthode spécifiée de BitFit ou de la méthode fortement paramétrée de LoRA, nous pouvons dériver une telle fonction pour représenter Delta Tuning (la dérivation détaillée est dans l'article).

Nous considérons la fonction Softmax et le terme de régularisation dans Delta Tuning comme des terminaux, et considérons le paramètre Delta comme la perte de fonctionnement de la variable de contrôle. Nous formulons le problème de Delta Tuning comme un problème de contrôle du temps discret, donc la direction avant dans. Le réglage Delta et la rétropropagation sont équivalents au calcul des processus comorphes dans le principe du maximum de Pontryagin. En résumé, le réglage incrémentiel peut être considéré comme le processus de recherche du contrôleur optimal pour un PLM pour une tâche spécifique en aval.

Notre analyse peut inspirer la conception de nouvelles méthodes de Delta Tuning, et nous démontrons également que l'intervention des paramètres delta sur le PLM est équivalente à la conception du contrôleur. En appliquant la théorie de la conception des contrôleurs, nous espérons proposer davantage de méthodes de réglage delta avec des garanties théoriques que la structure delta conçue est en principe interprétable sous une excitation suffisante du PLM.

Analyse expérimentale complète de Delta Tuning

En tant que méthode efficace pour stimuler et appeler du PLM à grande échelle, Delta Tuning a un énorme potentiel dans divers scénarios d'application pratiques. Dans cette section, nous menons des expériences systématiques pour mieux comprendre les propriétés des différentes méthodes traditionnelles de réglage delta.

1. Analyse des performances, de la convergence et de l'efficacité

Nous sélectionnons d'abord le réglage fin des paramètres complets et quatre méthodes de réglage Delta représentatives (y compris Prompt Tuning (PT), Prefix-Tuning (PF), LoRA (LR) et Adapter (AP) ) Performances, convergence, et les analyses d'efficacité sont minutieusement comparées. Afin de tester des capacités de modélisation linguistique plus diversifiées, nous avons sélectionné plus de 100 tâches typiques de PNL, notamment la classification de texte (telle que la classification des sentiments, l'inférence en langage naturel), la réponse aux questions (telle que la compréhension extractive en lecture), la génération de langage (telle que le résumé de texte). ) , dialogue) et d'autres tâches, et l'entrée et la sortie de toutes les tâches sont modélisées dans un format séquence à séquence, de sorte qu'il est pratique d'utiliser le même modèle (T5) pour modéliser uniformément toutes les tâches. Sauf que PT est testé sur T5-base et T5-large, d'autres méthodes sont testées sur T5-base.

Analyse des performances : Les résultats expérimentaux sont présentés dans le tableau ci-dessus. (1) En général, étant donné que les différentes méthodes de réglage Delta n'affinent que quelques paramètres, la difficulté d'optimisation. , donc dans la plupart des cas, ils ne peuvent pas égaler les performances de FT, mais l'écart entre les deux n'est pas insurmontable, ce qui démontre le potentiel d'applications à grande échelle d'une adaptation efficace des paramètres. (2) Bien que les éléments de conception des trois méthodes PF, LR et AP soient différents, leurs performances sont comparables. Il est possible que l’un d’entre eux soit plus performant que les autres (ou même FT) sur certaines tâches. Sur la base des résultats moyens, le classement des performances de toutes les méthodes est FT > LR > AP > PF > PT. Dans le même temps, nous avons également constaté que les performances de la méthode Delta Tuning ne sont pas cohérentes avec le nombre de ses paramètres réglables, c'est-à-dire que des paramètres plus réglables n'apporteront pas nécessairement de meilleures performances. En revanche, la conception structurelle spécifique de Delta Tuning. peut jouer un rôle plus important. (3) PT est la plus simple à mettre en œuvre parmi ces méthodes (c'est-à-dire qu'elle ne modifie pas la structure interne du modèle. Dans la plupart des cas, ses performances sont loin derrière les autres méthodes de réglage delta).

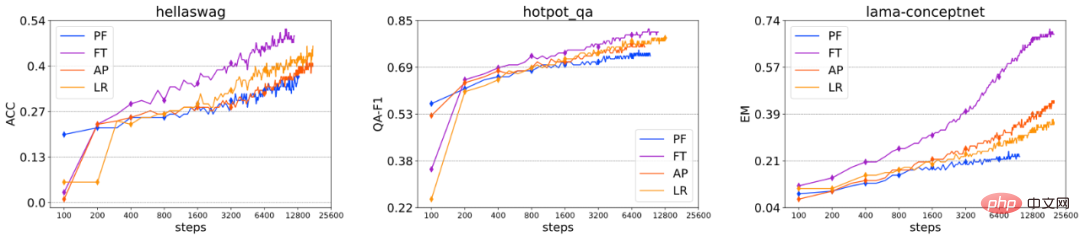
Analyse de convergence : Nous avons extrait les changements de performances de différentes méthodes de réglage fin sur certains ensembles de données à différents nombres d'étapes d'entraînement, car le PT converge trop lentement par rapport à d'autres méthodes, non inclus dans. la photo ci-dessus. Nous pouvons constater que, en général, l’ordre de vitesse de convergence de ces méthodes de réglage fin est : FT > AP ≈ LR > PF. Bien que PF possède le plus grand nombre de paramètres réglables parmi toutes les méthodes de réglage delta, il est toujours confronté à certaines difficultés de convergence, de sorte que la vitesse de convergence n'est pas directement liée au nombre de paramètres pouvant être ajustés avec précision. Lors d'expériences, nous avons également constaté que pour chaque méthode de Delta Tuning, les performances et la convergence ne sont pas sensibles au nombre de paramètres réglables, mais sont plus sensibles à la structure spécifique. Dans l’ensemble, nos expériences conduisent à des conclusions très similaires en termes de convergence et de performances globales, et ces conclusions sont bien étayées par des résultats sur un grand nombre d’ensembles de données.

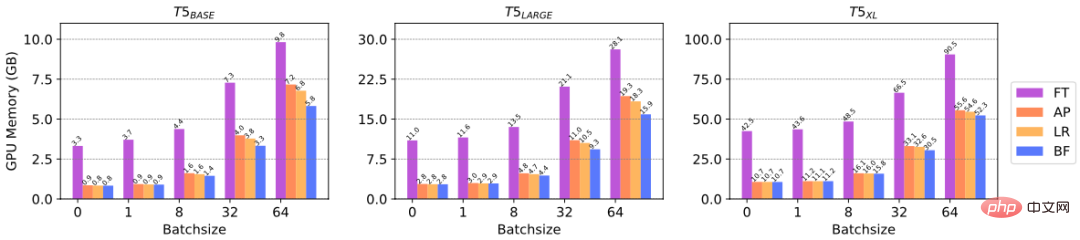
Analyse d'efficacité : Delta Tuning peut réduire le calcul du gradient des paramètres, économisant ainsi la mémoire GPU, reflétant l'efficacité des ressources informatiques. Afin de vérifier spécifiquement l'amélioration de l'efficacité du Delta Tuning sur la mémoire GPU, nous avons mené des expériences pour comparer la mémoire GPU consommée par différentes méthodes de Delta Tuning pour un réglage fin sur des PLM de différentes tailles. Plus précisément, nous avons sélectionné trois échelles de modèles T5, à savoir T5-base, T5-large et T5-xl, et testé le pic de mémoire GPU atteint avec différentes tailles de lots. Nous menons des expériences en utilisant un NVIDIA A100 (mémoire GPU maximale = 39,58 Go). D'après la figure ci-dessus, nous pouvons voir que lorsque la taille du lot est petite (par exemple, 1, 8), Delta Tuning peut économiser jusqu'à 3/4 de la mémoire GPU, et lorsque la taille du lot est grande, Delta Tuning peut économiser au moins 1/3 de la mémoire GPU. Les résultats ci-dessus reflètent l’efficacité de Delta Tuning en termes de ressources informatiques.

2. Analyse de composabilité

Considérant que différentes méthodes de Delta Tuning sont compatibles entre elles, ce qui signifie qu'elles peuvent être appliquées sur le même PLM en même temps. Nous avons donc étudié si une combinaison de Delta Tuning entraînerait une amélioration des performances. Plus précisément, nous avons exploré deux méthodes de combinaison : la combinaison simultanée et la combinaison séquentielle, et sélectionné trois méthodes représentatives de Delta Tuning, notamment Prompt Tuning, BitFit et Adapter.

Combinaison simultanée : nous explorons d'abord l'effet de l'application simultanée de trois méthodes de réglage Delta et menons des expériences sur 8 sous-tâches GLUE à l'aide de RoBERTa-large. Nous avons mené des expériences dans des scénarios à données complètes et à faibles ressources, et avons exploré l'impact des modèles de saisie artificiels sur les performances. Les modèles artificiels sont conçus pour combler le fossé entre la pré-formation et l'adaptation des tâches en aval.

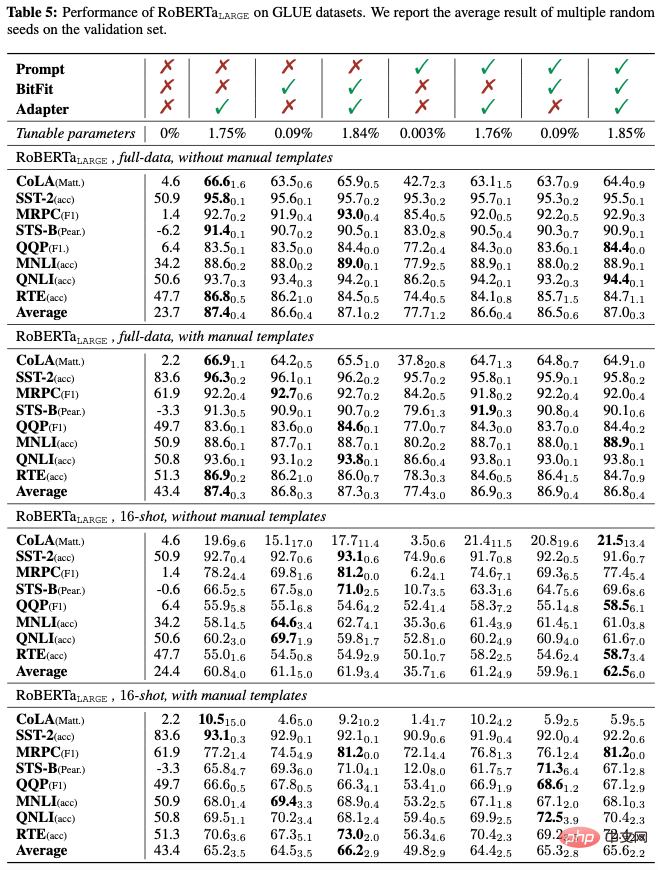
Comme le montre le tableau ci-dessus, (1) Que ce soit dans des scénarios de données complètes ou de faibles ressources, qu'il existe un modèle manuel ou non, l'introduction d'un adaptateur dans la combinaison de Delta Tuning est presque toujours aide les performances moyennes de GLUE ; (2) L'introduction de Prompt Tuning dans la combinaison nuit généralement aux performances moyennes, indiquant que Prompt Tuning peut être incompatible avec les deux autres méthodes de Delta Tuning (3) L'introduction de BitFit dans la combinaison améliore généralement les performances moyennes ; Les modèles manuels peuvent améliorer considérablement les performances du zéro tir (de 23,7 à 43,4) en comblant l'écart entre l'adaptation des tâches en aval et la pré-formation. Dans des environnements comportant peu de prises de vue, les modèles artificiels peuvent également améliorer considérablement les performances moyennes. Cependant, lorsque le signal de supervision de la formation est relativement abondant (dans le scénario de données complètes), l'introduction de modèles artificiels ne montre qu'une faible amélioration des performances, et peut même nuire aux performances.

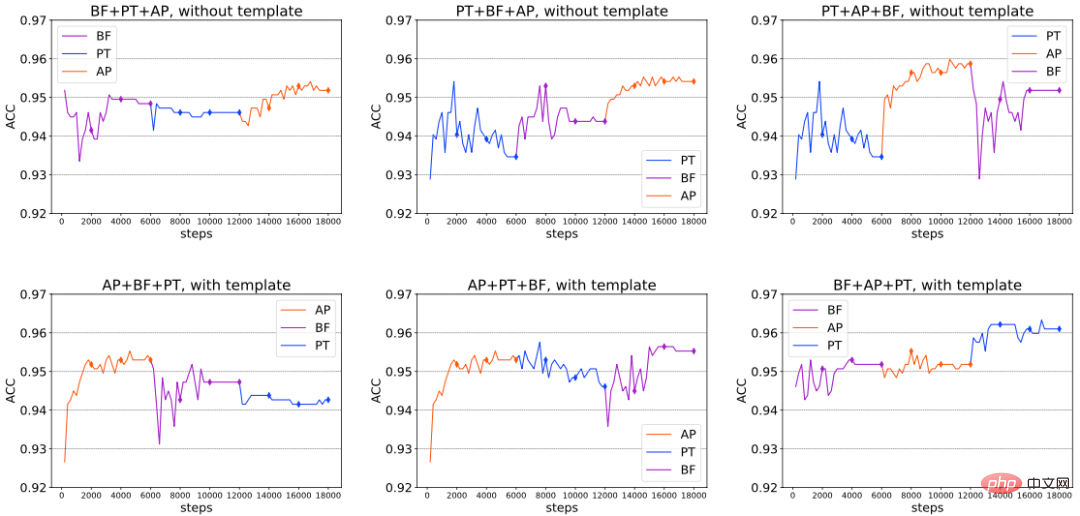
Combinaison séquentielle : en plus de la combinaison simultanée, nous avons étudié plus en détail la compatibilité des trois méthodes de réglage Delta ci-dessus lorsqu'elles sont introduites dans un certain ordre. Plus précisément, nous divisons l’ensemble de la mise au point en 3 étapes. À chaque étape, nous formons une méthode de Delta Tuning distincte ; à l'étape suivante, nous fixons les paramètres de Delta Tuning entraînés à l'étape précédente inchangés et optimisons uniquement les paramètres de Delta Tuning nouvellement introduits. Nous menons des expériences sur RoBERTa-large avec/sans modèles artificiels sur l'ensemble de données de classification des sentiments SST-2. Les résultats sont présentés dans la figure ci-dessous (extrait), à partir de laquelle nous pouvons conclure que dans certains cas, les performances globales peuvent être continuellement améliorées en introduisant continuellement de nouvelles méthodes de Delta Tuning, vérifiant ainsi les avantages de la combinaison séquentielle ; nous avons également constaté que, sous différents paramètres, il n'existe pas de séquence de combinaison optimale fixe. La combinaison optimale peut varier en fonction des différentes tâches en aval, de l'architecture du modèle utilisée et d'autres facteurs.

Analyse des écarts de généralisation : diverses méthodes de réglage fin ont différentes capacités de mémoire (mémorisation) et capacités de généralisation (généralisation) des données d'entraînement. À cette fin, nous rapportons l'écart de généralisation (effet d'ensemble de formation - effet d'ensemble de développement) de RoBERTa-large dans le contexte de données complètes. Les résultats sont présentés dans le tableau ci-dessous, à partir duquel nous pouvons voir que (1) Généralisation d'un seul. Méthode Delta Tuning L'écart est toujours plus petit que le réglage fin, ce qui signifie qu'un surparamétrage peut aider à mieux mémoriser (surajuster) les échantillons d'apprentissage. Le réglage rapide a tendance à présenter le plus petit écart de généralisation parmi toutes les méthodes de réglage delta. Considérant que chaque méthode de Delta Tuning peut bien généraliser et montrer des performances non triviales sur l'ensemble de développement, le surajustement de l'ensemble d'entraînement peut ne pas être une condition nécessaire pour une bonne généralisation (2) En général, la combinaison de plusieurs méthodes de Delta Tuning augmentera la généralisation ; écart, atteignant même le même niveau que le réglage fin complet. Cela montre que la mémorisation de l'ensemble d'apprentissage (mémorisation) peut ne pas nécessiter trop de réglage fin ; en d'autres termes, lorsque le PLM s'adapte aux tâches en aval, même si la capacité de réglage fin du modèle est faible, elle est toujours suffisante pour mémoriser. l'ensemble de formation ; (3) L'utilisation de modèles artificiels n'affecte généralement pas l'écart de généralisation.

3. Les performances changent à mesure que la taille du modèle augmente

Nous avons étudié l'impact de l'augmentation de la taille du modèle sur les performances de Delta Tuning. Récemment, certaines recherches ont révélé qu'à mesure que la taille du modèle PLM utilisé augmente, les performances du réglage rapide deviendront de plus en plus fortes, et peuvent même atteindre un niveau comparable à celui du réglage fin de l'ensemble des paramètres. Dans cette section, nous explorons si toutes les méthodes de réglage delta présentent le pouvoir de l'échelle. Plus précisément, nous avons mené des expériences sur trois tâches NLP typiques : MNLI, QNLI et SST-2, sélectionné trois PLM d'échelle croissante (T5-small, T5-base, T5-xxl) et évalué les performances de six méthodes de réglage delta représentatives ( Adaptateur, LoRA, Préfixe-Tuning, Prompt Tuning, Last Layer Tuning et Selective Module Tuning), les résultats sont présentés dans la figure ci-dessous.

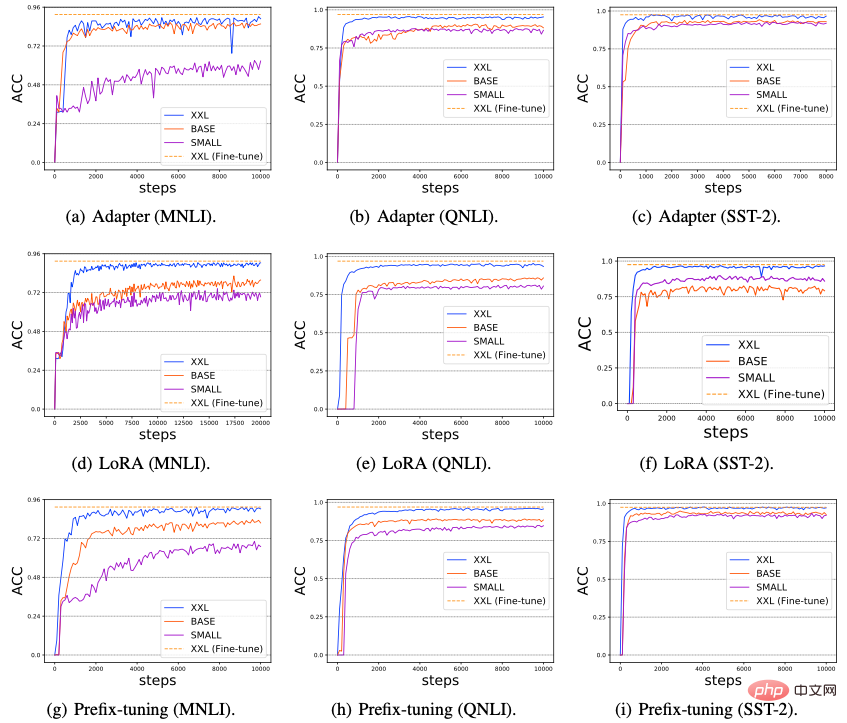
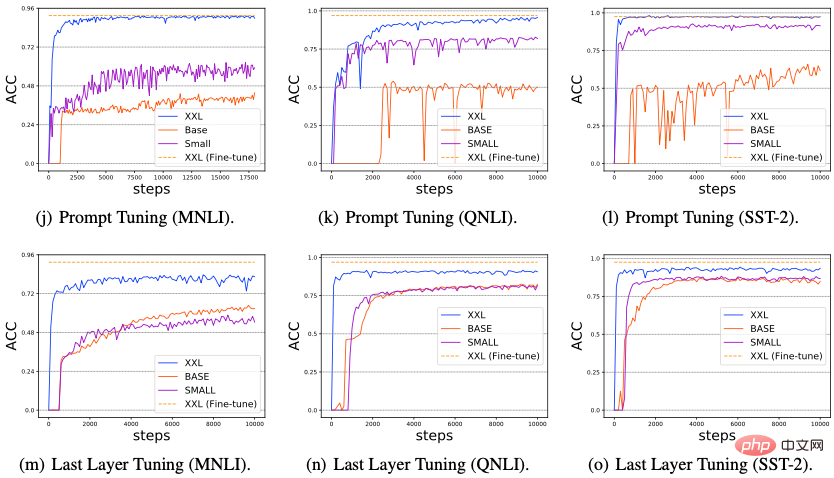
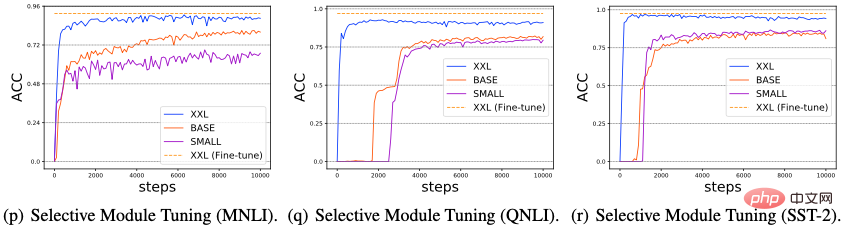
À partir de la figure (a-i), nous pouvons observer qu'à mesure que l'échelle du réseau PLM augmente, les performances et la convergence de toutes les méthodes de Delta Tuning diminuent de manière significative. une amélioration a été obtenue ; (2) De plus, la figure (j-l) montre que par rapport à d'autres méthodes de réglage delta, le réglage rapide fonctionne souvent mal sur les PLM à petite échelle (T5-small et T5-base). Cependant, d'autres méthodes de réglage Delta n'ont pas ce problème ; (3) Sur la base des résultats existants, dans les figures 11 (m-o) et (p-r), nous concevons en outre deux méthodes de réglage Delta : le réglage de la dernière couche et le réglage sélectif du module. Pour le réglage de la dernière couche, nous ajustons uniquement la dernière couche de l'encodeur T5 ; pour le réglage sélectif du module, nous sélectionnons au hasard certains modules du modèle T5 pour un réglage précis. Les deux méthodes donnent d'excellents résultats, en particulier lorsque l'échelle du PLM est très grande, avec un réglage sélectif du module légèrement meilleur que le réglage de la dernière couche. Ces résultats suggèrent que limiter les paramètres affinables à une couche spécifique n’est peut-être pas une bonne stratégie. D’un autre côté, lorsque l’échelle du PLM devient très importante, un réglage fin en sélectionnant aléatoirement des modules sur différentes couches peut permettre d’obtenir d’excellentes performances. Dans l'ensemble, les résultats ci-dessus indiquent qu'à mesure que la taille du modèle PLM augmente, des améliorations significatives des performances/vitesse de convergence de diverses méthodes de réglage fin peuvent être un phénomène courant dans Delta Tuning. Nous pensons que ce phénomène existe parce que les PLM plus grands ont généralement des dimensions intrinsèques plus petites (dimension intrinsèque). Par conséquent, seul l'ajustement de quelques paramètres peut obtenir des capacités de représentation suffisamment fortes pour être mises en œuvre dans des tâches en aval, en plus des modèles surparamétrés. peut être moins susceptible de tomber dans des optima locaux lors de l'optimisation en aval, accélérant ainsi la convergence.

4. Transférabilité inter-tâches

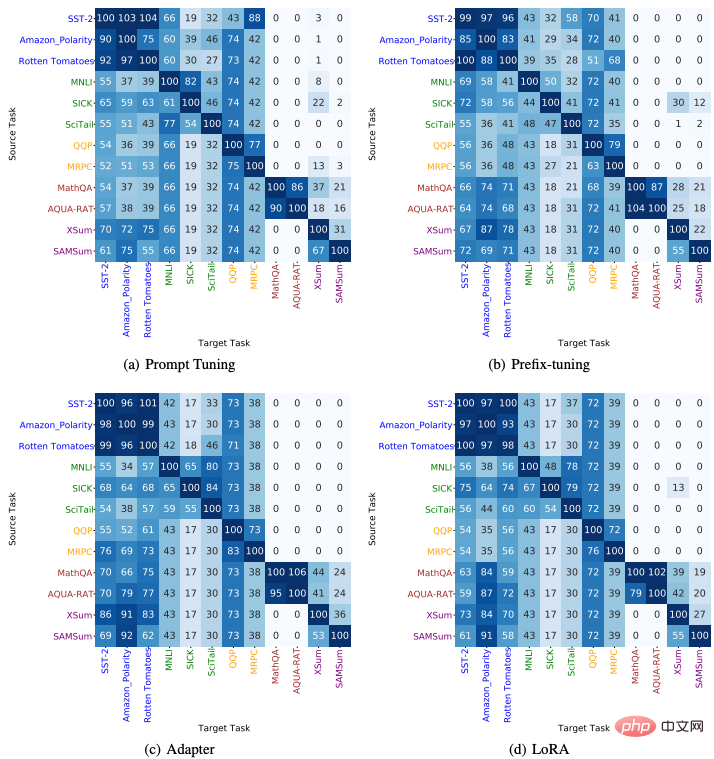
Nous avons étudié la transférabilité des méthodes de Delta Tuning entre différentes tâches en aval. Plus précisément, nous avons adopté 4 méthodes de Delta Tuning (Prompt Tuning, Prefix- Tuning, Adapter et LoRA) et. 12 tâches PNL de 5 types différents (y compris l'analyse des sentiments, le raisonnement en langage naturel, la reconnaissance de paraphrase, les questions et réponses, le résumé) et transférer les paramètres Delta formés sur la tâche source vers la tâche cible, tester l'effet de migration zéro. Les résultats sont présentés dans la figure ci-dessous, à partir de laquelle nous pouvons observer : (1) Pour les tâches appartenant à la même catégorie, le transfert entre elles fonctionne généralement bien ; (2) Pour les tâches de types différents, les performances de transfert entre elles sont médiocres ; 3) De plus, nous avons constaté que les paramètres Delta formés à partir des tâches de génération de texte (telles que les questions, réponses et résumés) peuvent être transférés aux tâches d'analyse des sentiments et atteindre d'excellentes performances, ce qui indique que la tâche de génération de texte peut être une tâche plus complexe. Les compétences linguistiques requises pour la tâche peuvent inclure des compétences en analyse des sentiments.

Application Delta Tuning

Entraînement rapide et gain d'espace de stockage. Les modèles de transformateurs, bien que intrinsèquement parallélisables, sont très lents à entraîner en raison de leur taille. Bien que le taux de convergence du Delta Tuning puisse être plus lent que le réglage fin traditionnel des paramètres complets, la vitesse d'entraînement du Delta Tuning est également considérablement améliorée car l'effort de calcul des paramètres affinés pendant la rétropropagation est considérablement réduit. Des recherches antérieures ont vérifié que l'utilisation d'adaptateurs pour le réglage en aval peut réduire le temps de formation jusqu'à 40 % tout en maintenant des performances comparables à un réglage précis des paramètres complets. En raison de leur légèreté, les paramètres Delta formés peuvent également économiser de l'espace de stockage, facilitant ainsi le partage entre praticiens et favorisant le transfert de connaissances.

Apprentissage multi-tâches. Construire des systèmes généraux d’intelligence artificielle est depuis longtemps un objectif des chercheurs. Récemment, de très grands PLM (par exemple, GPT-3) ont démontré leur incroyable capacité à s'adapter simultanément à différentes distributions de données et à faciliter les performances en aval sur une variété de tâches. Par conséquent, à l’ère de la pré-formation à grande échelle, l’apprentissage multitâche fait l’objet de plus en plus d’attention. En tant qu'alternative efficace aux méthodes de réglage fin de tous les paramètres, Delta Tuning possède d'excellentes capacités d'apprentissage multitâches tout en conservant un stockage supplémentaire relativement faible. Les applications réussies incluent l’apprentissage multilingue, la compréhension écrite, etc. De plus, Delta Tuning devrait également constituer une solution potentielle à l’oubli catastrophique dans l’apprentissage continu. Les capacités linguistiques acquises lors de la pré-formation sont stockées dans les paramètres du modèle. Par conséquent, la mise à jour de tous les paramètres du PLM sans régularisation peut conduire à des oublis graves et catastrophiques lorsque le PLM est entraîné séquentiellement sur une séquence de tâches. Étant donné que Delta Tuning n’ajuste que des paramètres minimaux, cela pourrait constituer une solution potentielle pour atténuer le problème catastrophique de l’oubli.

Service de modèles centralisé et calcul parallèle. Les très gros PLM sont souvent publiés en tant que service, c'est-à-dire que les utilisateurs consomment le grand modèle en interagissant avec les API publiées par le fournisseur de modèles, plutôt qu'en stockant le grand modèle localement. Compte tenu du coût de communication insupportable entre les utilisateurs et les fournisseurs de services, le Delta Tuning est clairement une option plus compétitive que le réglage fin traditionnel de tous les paramètres en raison de sa légèreté. D'une part, les fournisseurs de services peuvent prendre en charge les tâches en aval nécessaires à la formation de plusieurs utilisateurs tout en consommant moins d'espace informatique et de stockage. De plus, étant donné que certains algorithmes de Delta Tuning sont intrinsèquement parallélisables (tels que le réglage d'invite et le réglage de préfixe, etc.), Delta Tuning peut permettre la formation/le test en parallèle d'échantillons provenant de plusieurs utilisateurs dans le même lot (informatique parallèle en lots). . Des travaux récents ont également montré que la plupart des méthodes de réglage delta, si elles ne sont pas intrinsèquement parallélisables, peuvent être modifiées d'une certaine manière pour prendre en charge le calcul parallèle. D'un autre côté, lorsque les gradients du modèle central ne sont pas disponibles pour l'utilisateur, Delta Tuning est toujours capable d'optimiser les grands PLM grâce à un algorithme de boîte noire sans dégradé et fait uniquement appel à l'API d'inférence de modèle.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!