Maison >Périphériques technologiques >IA >Le modèle de diffusion récemment populaire, la première revue des modèles de génération de diffusion !
Le modèle de diffusion récemment populaire, la première revue des modèles de génération de diffusion !
- PHPzavant
- 2023-04-09 20:31:011674parcourir

Cette revue (Diffusion Models: A Comprehensive Survey of Methods and Applications) provient de Ming-Hsuan Yang de l'Université de Californie et de Google Research, du laboratoire Cui Bin de l'Université de Pékin et d'équipes de recherche telles que CMU, UCLA, et l'Institut de recherche Mila de Montréal. Pour la première fois, un résumé et une analyse complets des modèles de diffusion existants ont été réalisés, à partir de la classification détaillée de l'algorithme du modèle de diffusion, de son association avec cinq autres modèles génératifs majeurs et de son application dans sept modèles majeurs. Enfin, le modèle de diffusion a été proposé en tenant compte des limites existantes du modèle et des orientations de développement futures.
Lien de l'article : https://arxiv.org/abs/2209.00796 Cet examen des modèles de diffusion résumé de la classification des papiers lien github : https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy
1 Introduction
Les modèles de diffusion sont le nouveau SOTA dans les modèles génératifs profonds. Le modèle de diffusion surpasse le SOTA : GAN original dans les tâches de génération d'images et présente d'excellentes performances dans de nombreux domaines d'application, tels que la vision par ordinateur, la PNL, le traitement du signal de forme d'onde, la modélisation multimodale, la modélisation de graphiques moléculaires et la modélisation de séries chronologiques, antagonistes. purification, etc De plus, les modèles de diffusion sont étroitement liés à d’autres domaines de recherche, tels que l’apprentissage robuste, l’apprentissage par représentation et l’apprentissage par renforcement.
Cependant, le modèle de diffusion original présente également des défauts. Sa vitesse d'échantillonnage est lente, nécessitant généralement des milliers d'étapes d'évaluation pour tirer un échantillon ; son estimation du maximum de vraisemblance n'est pas comparable à celle des modèles basés sur la vraisemblance ; accéder à différents types de données est difficile. De nos jours, de nombreuses études ont déployé de nombreux efforts pour résoudre les limitations ci-dessus du point de vue des applications pratiques, ou ont analysé les capacités du modèle d'un point de vue théorique.
Cependant, il manque un examen systématique des avancées récentes dans les modèles de diffusion, des algorithmes aux applications. Pour refléter les progrès dans ce domaine en croissance rapide, nous présentons la première revue complète des modèles de diffusion. Nous envisageons que nos travaux mettront en lumière les considérations de conception et les méthodes avancées des modèles de diffusion, démontreront leurs applications dans différents domaines et indiqueront les orientations de recherche futures. Le résumé de cette revue est présenté ci-dessous :
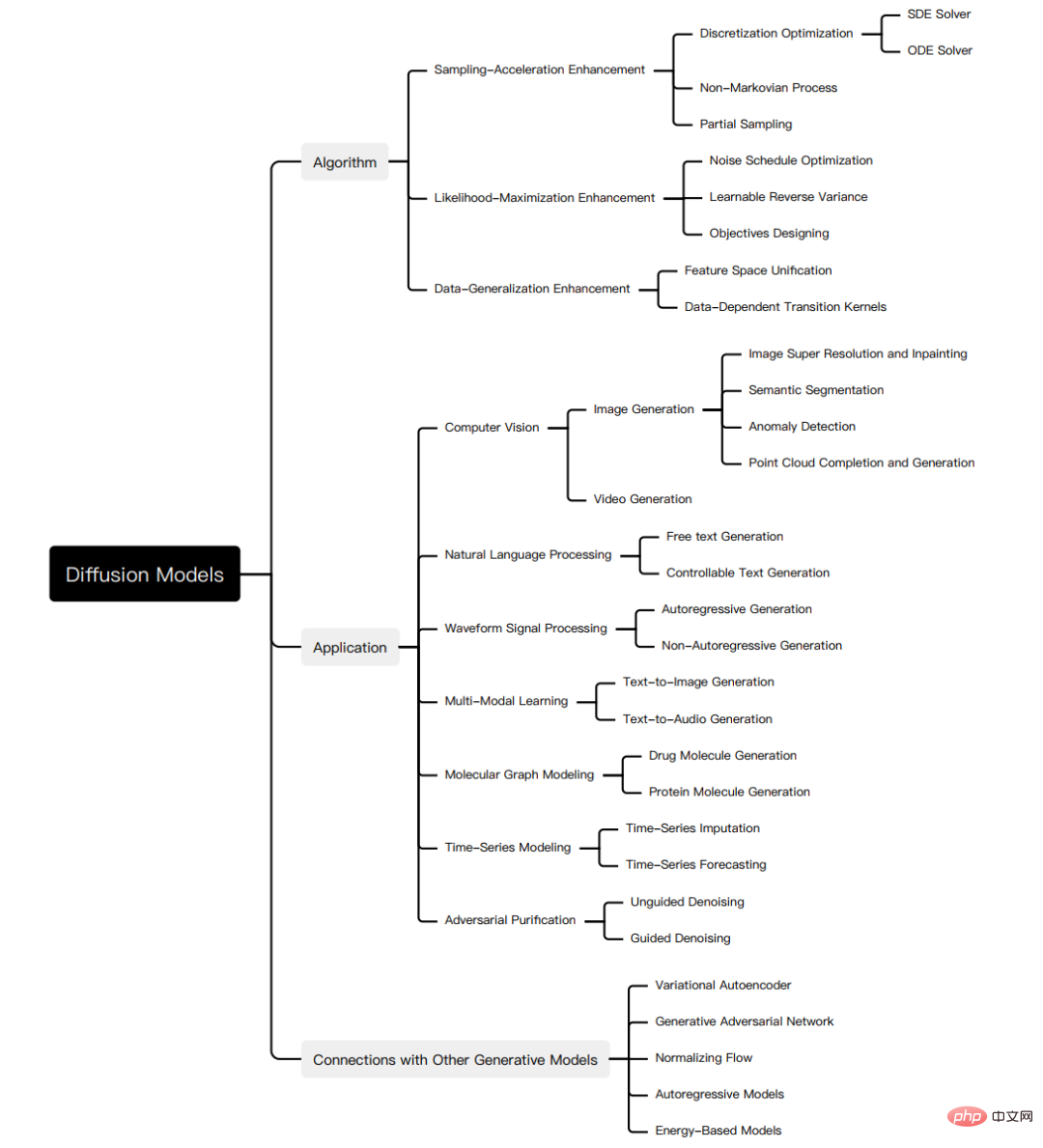
Bien que le modèle de diffusion ait d'excellentes performances dans diverses tâches, il a encore ses propres défauts et de nombreuses études ont amélioré le modèle de diffusion.
Afin de clarifier systématiquement les progrès de la recherche sur les modèles de diffusion, nous avons résumé les trois principales lacunes du modèle de diffusion original, la vitesse d'échantillonnage lente, la différence de vraisemblance maximale et la faible capacité de généralisation des données, et avons proposé des recherches sur l'amélioration des modèles de diffusion. Divisé en trois catégories correspondantes : amélioration de la vitesse d’échantillonnage, amélioration du maximum de vraisemblance et amélioration de la généralisation des données.
Nous expliquons d'abord la motivation à l'amélioration, puis classons davantage la recherche dans chaque direction d'amélioration en fonction des caractéristiques de la méthode, afin de montrer clairement les liens et les différences entre les méthodes. Ici, nous sélectionnons uniquement quelques méthodes importantes à titre d'exemples. Chaque type de méthode est présenté en détail dans notre travail, comme le montre la figure :
Après avoir analysé les trois types de modèles de diffusion, nous présenterons les cinq autres. modèles génératifs GAN, VAE, modèle autorégressif, flux normalisant et modèle basé sur l'énergie.
Compte tenu des excellentes propriétés du modèle de diffusion, les chercheurs ont combiné le modèle de diffusion avec d'autres modèles génératifs en fonction de ses caractéristiques. Par conséquent, afin de démontrer davantage les caractéristiques et les travaux d'amélioration du modèle de diffusion, nous avons introduit le modèle de diffusion. et d'autres modèles génératifs en détail La combinaison de modèles fonctionne et illustre les améliorations par rapport au modèle génératif d'origine.
Le modèle de diffusion a d'excellentes performances dans de nombreux domaines, et étant donné que le modèle de diffusion présente différentes déformations dans les applications dans différents domaines, nous avons systématiquement introduit la recherche d'application du modèle de diffusion, y compris les domaines suivants : vision par ordinateur, PNL, traitement du signal de forme d'onde. , modélisation multimodale, modélisation de graphes moléculaires, modélisation de séries chronologiques, purification contradictoire. Pour chaque tâche, nous définissons la tâche et présentons le travail qui utilise le modèle de diffusion pour gérer la tâche Nous résumons les principales contributions de ce travail comme suit :
.- Nouvelle méthode de classification : Nous proposons une nouvelle taxonomie systématique des modèles de diffusion et de leurs applications. Plus précisément, nous divisons les modèles en trois catégories : amélioration de la vitesse d'échantillonnage, amélioration de l'estimation du maximum de vraisemblance et amélioration de la généralisation des données. De plus, nous classons les applications des modèles de diffusion en sept catégories : vision par ordinateur, PNL, traitement du signal de forme d'onde, modélisation multimodale, modélisation de graphes moléculaires, modélisation de séries chronologiques et purification contradictoire.
- Comprehensive Review : Nous fournissons le premier aperçu complet des modèles de diffusion modernes et de leurs applications. Nous présentons les principales améliorations de chaque modèle de diffusion, effectuons les comparaisons nécessaires avec le modèle original et résumons les articles correspondants. Pour chaque type d'application des modèles de diffusion, nous présentons les principaux problèmes abordés par les modèles de diffusion et expliquons comment ils résolvent ces problèmes.
- Orientations futures de la recherche : Nous soulevons des questions ouvertes pour les recherches futures et fournissons quelques suggestions pour le développement futur des modèles de diffusion en termes d'algorithmes et d'applications.
2 Bases du modèle de diffusion
Un problème central de la modélisation générative est le compromis entre la flexibilité du modèle et la calculabilité. L'idée de base du modèle de diffusion est de perturber systématiquement la distribution des données via le processus de diffusion directe, puis de restaurer la distribution des données en apprenant le processus de diffusion inverse, produisant ainsi un modèle très flexible et facile à calculer. modèle génératif.
(1) Modèles probabilistes de diffusion de débruitage (DDPM)
Un DDPM se compose de deux chaînes de Markov paramétrées et utilise l'inférence variationnelle pour générer une distribution cohérente avec les données d'origine après un échantillon de temps fini. La fonction de la chaîne directe est de perturber les données. Elle ajoute progressivement du bruit gaussien aux données selon le programme de bruit prédéfini jusqu'à ce que la distribution des données tende vers la distribution antérieure, c'est-à-dire la distribution gaussienne standard. La chaîne arrière part d'un a priori donné et utilise un noyau de transformation gaussienne paramétré, apprenant à restaurer progressivement la distribution des données d'origine. représente les données d'origine et leur distribution, alors la distribution de la chaîne directe peut être exprimée par la formule suivante :
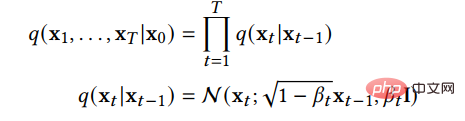
Cela montre que la chaîne directe est un processus de Markov, qui est un échantillon après avoir ajouté t étapes de bruit, et est donné à l'avance Certains paramètres qui contrôlent la progression du bruit. Lorsqu'elle tend vers 1, elle peut être considérée approximativement comme obéissant à la distribution gaussienne standard. Lorsqu'il est petit, le noyau de transfert du processus inverse peut être approximativement considéré comme gaussien :
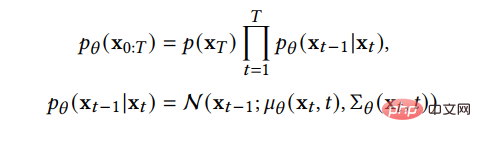
Nous pouvons apprendre la borne inférieure variationnelle comme fonction de perte :
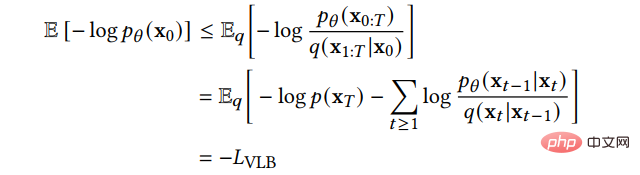
(2) Score- Modèles génératifs basés (SGM)
Le DDPM ci-dessus peut être considéré comme la forme discrète de SGM. SGM construit une équation différentielle stochastique (SDE) pour perturber en douceur la distribution des données et transformer la distribution des données d'origine en une distribution antérieure connue :
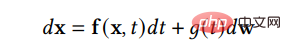
et une SDE inverse correspondante pour transformer la distribution antérieure en arrière Distribution des données brutes :
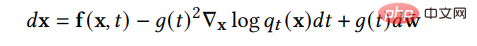
Ainsi, pour inverser le processus de diffusion et générer des données, la seule information dont nous avons besoin est la fonction fractionnaire à chaque instant. En utilisant la technique de correspondance de score, nous pouvons apprendre la fonction de score grâce à la fonction de perte suivante :
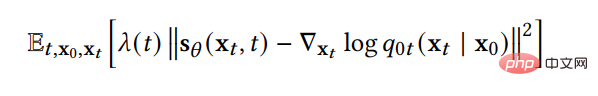
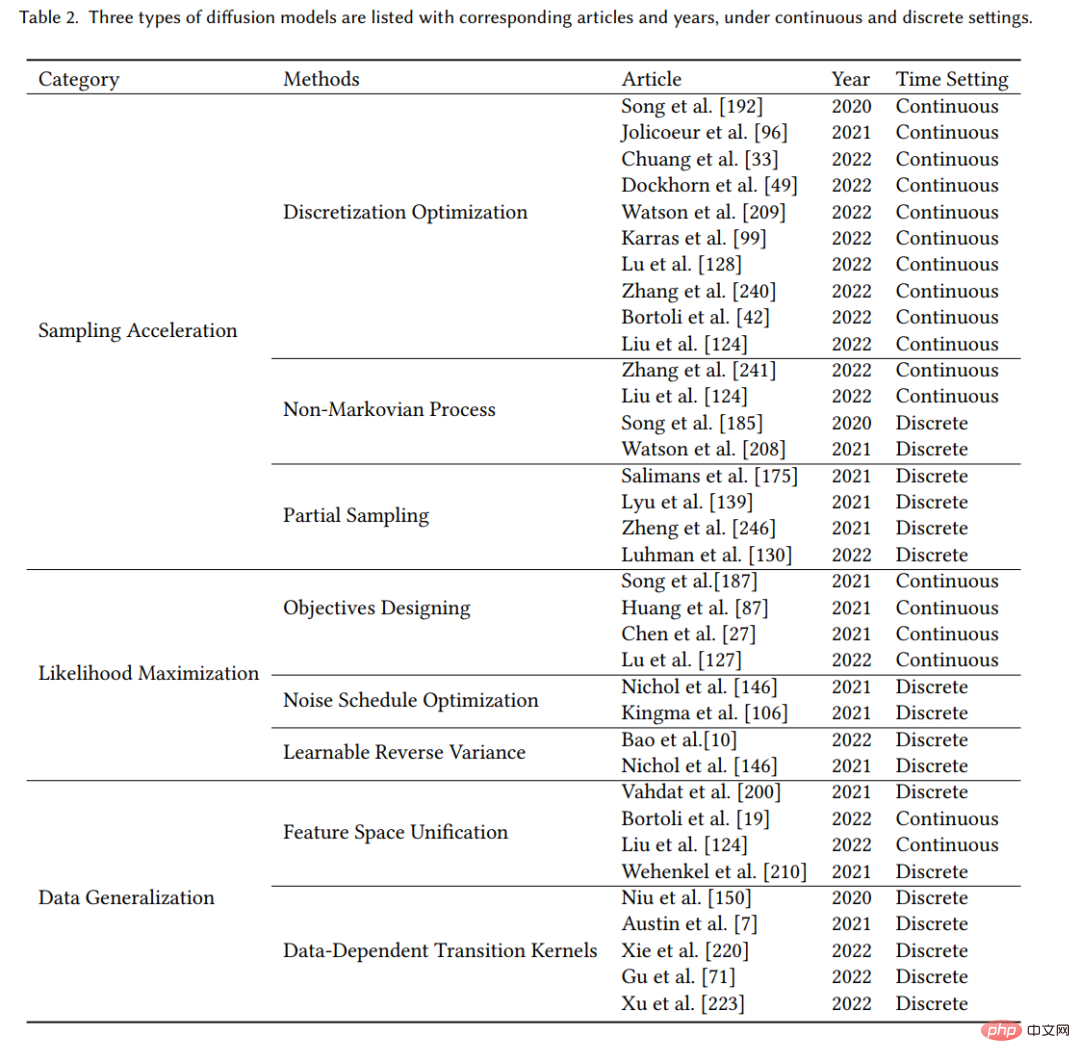
Pour une introduction plus approfondie aux deux méthodes et à la relation entre les deux, veuillez consulter notre article. Les trois principaux défauts du modèle de diffusion original sont la lenteur de l’échantillonnage, une faible maximisation de la vraisemblance et une faible capacité de généralisation des données. De nombreuses études récentes ont abordé ces lacunes, c'est pourquoi nous classons les modèles de diffusion améliorés en trois catégories : amélioration de la vitesse d'échantillonnage, amélioration du maximum de vraisemblance et amélioration de la généralisation des données. Dans les trois, quatre et cinq prochaines sections, nous présenterons en détail ces trois types de modèles.
3 Méthode d'accélération de l'échantillonnage
Lorsqu'il est appliqué, afin d'optimiser la qualité du nouvel échantillon, le modèle de diffusion nécessite souvent des milliers d'étapes de calcul pour obtenir un nouvel échantillon. Cela limite la valeur d’application pratique du modèle de diffusion, car dans l’application réelle, nous devons souvent générer un grand nombre de nouveaux échantillons pour fournir des matériaux pour l’étape suivante du traitement.
Les chercheurs ont mené de nombreuses recherches pour améliorer la vitesse d'échantillonnage du modèle de diffusion. Nous décrivons ces études en détail. Nous l'affinons en trois méthodes : optimisation de la discrétisation, processus non markovien et échantillonnage partiel.
(1) La méthode d'optimisation de discrétisation optimise la méthode de résolution du SDE de diffusion. Étant donné que la résolution de SDE complexes ne peut en réalité utiliser que des solutions discrètes pour se rapprocher de la solution réelle, ce type de méthode tente d'optimiser la méthode de discrétisation de SDE afin de réduire le nombre d'étapes discrètes tout en garantissant la qualité des échantillons. SGM propose une méthode générale pour résoudre le processus inverse, c'est-à-dire que la même méthode de discrétisation est adoptée pour les processus avant et arrière. Si la méthode de discrétisation du SDE direct est donnée :
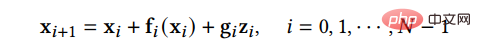
alors nous pouvons discrétiser le SDE inverse de la même manière :
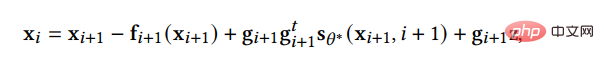
Cette méthode est légèrement meilleure que le DDPM naïf. De plus, SGM ajoute un correcteur au solveur SDE afin que les échantillons générés à chaque étape aient la bonne distribution. À chaque étape de la solution, une fois que le solveur a reçu un échantillon, le redresseur utilise une méthode de Monte Carlo par chaîne de Markov pour redresser la distribution de l'échantillon qui vient d'être généré. Les expériences montrent que l’ajout d’un correcteur au solveur est plus efficace que l’augmentation directe du nombre d’étapes dans le solveur.
(2) La méthode du processus non markovien dépasse les limites du processus markovien original. Chaque étape du processus inverse peut s'appuyer sur davantage d'échantillons passés pour prédire de nouveaux échantillons, elle peut donc également être effectuée en fonction de la taille de l'étape. est grande, produit de meilleures prédictions, accélérant ainsi le processus d’échantillonnage. Parmi eux, l'ouvrage principal DDIM ne suppose plus que le processus direct est un processus de Markov, mais obéit à la distribution suivante :
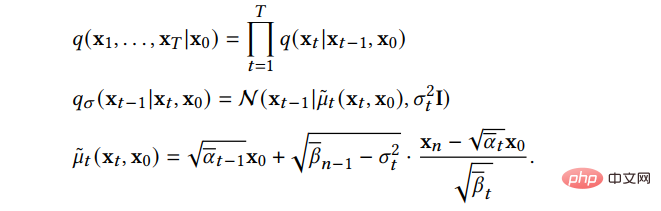
Le processus d'échantillonnage de DDIM peut être considéré comme une équation différentielle régulière divine discrétisée, et son Le processus d'échantillonnage est plus efficace et prend en charge l'interpolation des échantillons. Des recherches plus approfondies ont montré que DDIM peut être considéré comme un cas particulier du modèle de diffusion sur collecteur PNDM.
(3) La méthode d'échantillonnage partiel réduit directement le temps d'échantillonnage en ignorant une partie des nœuds temporels dans le processus de génération et en utilisant uniquement les nœuds temporels restants pour générer des échantillons. Par exemple, Progressive Distillation distille un modèle de diffusion plus efficace à partir d’un modèle de diffusion entraîné. Pour un modèle de diffusion entraîné, Progressive Distillation recyclera un modèle de diffusion afin qu'une étape du nouveau modèle de diffusion corresponde aux deux étapes du modèle de diffusion entraîné, afin que le nouveau modèle puisse économiser la moitié du processus d'échantillonnage de l'ancien modèle. L'algorithme spécifique est le suivant :

La boucle continue de ce processus de distillation peut réduire les étapes d'échantillonnage de manière exponentielle.
4 Apprentissage semi-supervisé, purification contradictoire. Étant donné que le log de vraisemblance est difficile à calculer directement, la recherche se concentre principalement sur l’optimisation et l’analyse des limites inférieures variationnelles (VLB). Nous élaborons des modèles qui améliorent les estimations du maximum de vraisemblance des modèles de diffusion. Nous l'affinons en trois catégories de méthodes : conception d'objectifs, optimisation du programme de bruit et variance inverse apprenable.
(1) La méthode de conception d'objectifs utilise la diffusion SDE pour déduire la relation entre la log de vraisemblance des données générées et la fonction de perte correspondant à la fonction de score. De cette manière, en concevant de manière appropriée la fonction de perte, la VLB et la log-vraisemblance peuvent être maximisées. Song et al. ont prouvé que la fonction de pondération de la fonction de perte peut être conçue de telle sorte que la valeur de la fonction de vraisemblance de l'échantillon généré par le SDE inversé du plug-in soit inférieure ou égale à la valeur de la fonction de perte, c'est-à-dire que la fonction de perte est la limite supérieure de la fonction de vraisemblance. La fonction de perte pour l'ajustement de la fonction fractionnaire est la suivante :
Il suffit de définir la fonction de poids sur le coefficient de diffusion g(t) pour que la fonction de perte devienne la VLB de la fonction de vraisemblance, c'est-à-dire :
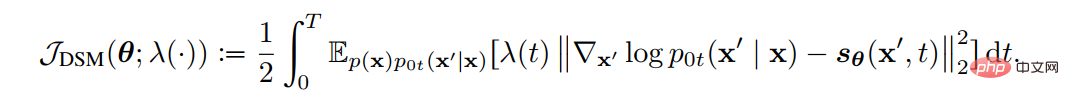
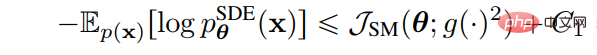 (2) L'optimisation du programme de bruit augmente le VLB en concevant ou en apprenant le programme de bruit du processus avancé. VDM prouve que lorsque les étapes discrètes tendent vers l'infini, la fonction de perte est complètement déterminée par le point final de la fonction de rapport signal sur bruit SNR(t) :
(2) L'optimisation du programme de bruit augmente le VLB en concevant ou en apprenant le programme de bruit du processus avancé. VDM prouve que lorsque les étapes discrètes tendent vers l'infini, la fonction de perte est complètement déterminée par le point final de la fonction de rapport signal sur bruit SNR(t) :
Puis, lorsque les étapes discrètes tendent vers l'infini, le signal La fonction de rapport signal/bruit peut être apprise en optimisant le point final de SNR(t) VLB, et d'autres aspects du modèle sont améliorés en apprenant la valeur de la fonction dans la partie médiane de la fonction de rapport signal/bruit. 3. La méthode Learnable Reverse Variance apprend la variance du processus inverse, réduisant ainsi les erreurs d'ajustement et peut maximiser efficacement le VLB. Analytic-DPM prouve qu'il existe une attente et une variance optimales dans le processus inverse dans DDPM et DDIM :
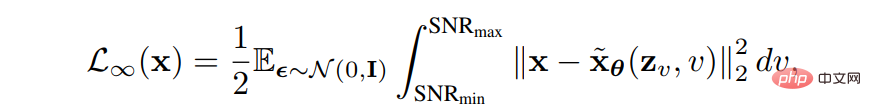
En utilisant la formule ci-dessus et la fonction de score entraînée, compte tenu des conditions du processus direct, l'Excellent VLB optimal peut être atteint approximativement.
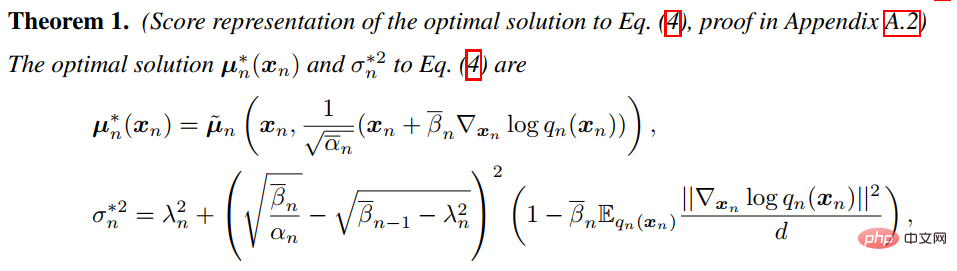
Plusieurs travaux de recherche ont généralisé le modèle de diffusion à des modèles adaptés à d'autres types de données, et nous expliquons ces méthodes en détail. Nous le classons en deux types de méthodes : l'unification de l'espace de fonctionnalités et les noyaux de transition dépendant des données.
(1) La méthode Feature Space Unification convertit les données en un espace latent unifié, puis les diffuse sur l'espace latent. Le LSGM propose de convertir les données en un espace latent continu grâce au framework VAE puis de les diffuser sur celui-ci. La difficulté de cette méthode est de savoir comment entraîner simultanément la VAE et le modèle de diffusion. LSGM montre que puisque le prior sous-jacent est insoluble, la perte d'appariement fractionnaire ne s'applique plus. LSGM utilise directement la fonction de perte traditionnelle ELBO dans VAE comme fonction de perte et dérive la relation entre ELBO et la correspondance des scores :
Cette formule est valable dans le sens d'ignorer les constantes. En paramétrant la fonction fractionnaire de l'échantillon dans le processus de diffusion, LSGM peut apprendre et optimiser efficacement ELBO.
(2) La méthode Data-Dependent Transition Kernels conçoit les noyaux de transition dans le processus de diffusion en fonction des caractéristiques du type de données, afin que le modèle de diffusion puisse être directement appliqué à des types de données spécifiques. D3PM a conçu un noyau de transition pour les données discrètes, qui peut être défini sur une marche aléatoire paresseuse, un état d'absorption, etc. GEODIFF a conçu un réseau neuronal de graphes invariants en translation-rotation pour les données de graphes moléculaires 3D et a prouvé que la distribution initiale invariante et le noyau de transition peuvent dériver une distribution marginale invariante. Supposons qu'il s'agisse d'une transformation translation-rotation, telle que :
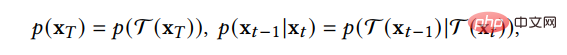
Ensuite, l'échantillon de distribution généré a également une invariance translation-rotation :
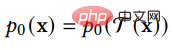
6 La connexion avec d'autres modèles génératifs
est ci-dessous Dans chaque sous-section, nous présentons d'abord les cinq autres catégories importantes de modèles génératifs et analysons leurs avantages et leurs limites. Nous présentons ensuite comment les modèles de diffusion leur sont liés et illustrons comment ces modèles génératifs peuvent être améliorés en incorporant des modèles de diffusion. La relation entre VAE, GAN, modèle autorégressif, flux normalisant, modèle basé sur l'énergie et modèle de diffusion est illustrée dans la figure ci-dessous :
- DDPM peut être considérée comme une VAE markovienne hiérarchique (VAE markovienne hiérarchique ). Mais il existe aussi des différences entre DDPM et VAE générale. En tant que VAE, l'encodeur et le décodeur de DDPM obéissent tous deux à la distribution gaussienne et possèdent des lignes de Markov ; la dimension de ses variables cachées est la même que la dimension des données. Toutes les couches du décodeur partagent un réseau neuronal ;
- DDPM peut aider GAN à résoudre le problème de la formation instable. Étant donné que les données se trouvent dans une variété de faible dimension dans un espace de grande dimension, la distribution des données générées par GAN présente un faible chevauchement avec la distribution des données réelles, ce qui entraîne une formation instable. Le modèle de diffusion fournit un processus d'ajout systématique de bruit. Il ajoute du bruit aux données générées et aux données réelles via le modèle de diffusion, puis envoie les données ajoutées au discriminateur. Cela peut résoudre efficacement le problème de l'incapacité du GAN à s'entraîner. et la formation étant instable.
- La normalisation du flux convertit les données en une distribution antérieure via une fonction de bijection. Cette approche limite la capacité d'expression du flux normalisant, ce qui entraîne de mauvais résultats d'application. Le modèle de diffusion analogique ajoute du bruit à l'encodeur, ce qui peut augmenter la capacité d'expression du flux de normalisation. D'un autre point de vue, cette approche consiste à étendre le modèle de diffusion à un modèle qui peut également être appris dans le processus direct.
- Le modèle autorégressif doit garantir que les données ont une certaine structure, ce qui rend très difficile la conception et le paramétrage du modèle autorégressif. La formation de modèles de diffusion a inspiré la formation de modèles autorégressifs, qui évitent les difficultés de conception grâce à des méthodes de formation spécifiques.
- Le modèle basé sur l'énergie modélise directement la distribution des données originales, mais la modélisation directe rend l'apprentissage et l'échantillonnage difficiles. En utilisant la probabilité de récupération par diffusion, le modèle peut d'abord ajouter un léger bruit à l'échantillon, puis déduire la distribution de l'échantillon d'origine à partir de la distribution de l'échantillon légèrement bruitée, ce qui rend le processus d'apprentissage et d'échantillonnage plus simple et plus stable.
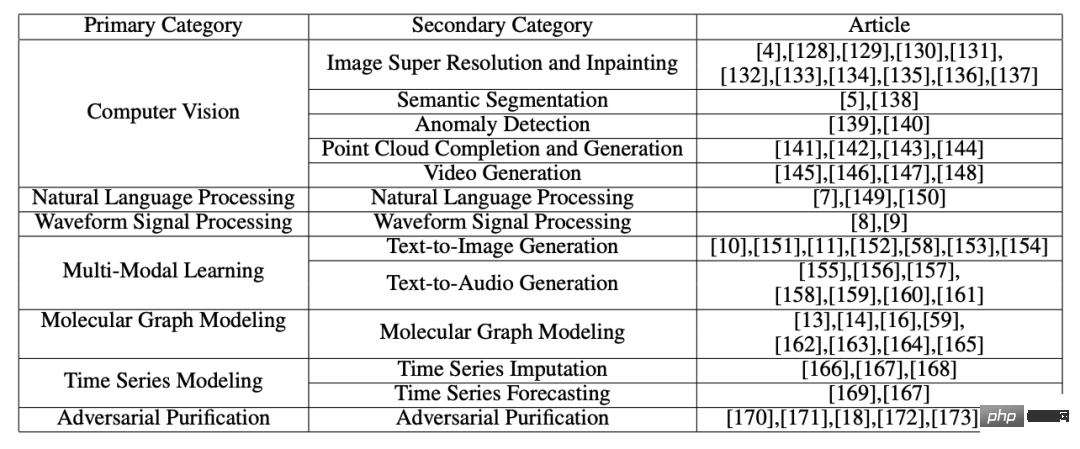
7 Applications du modèle de diffusion
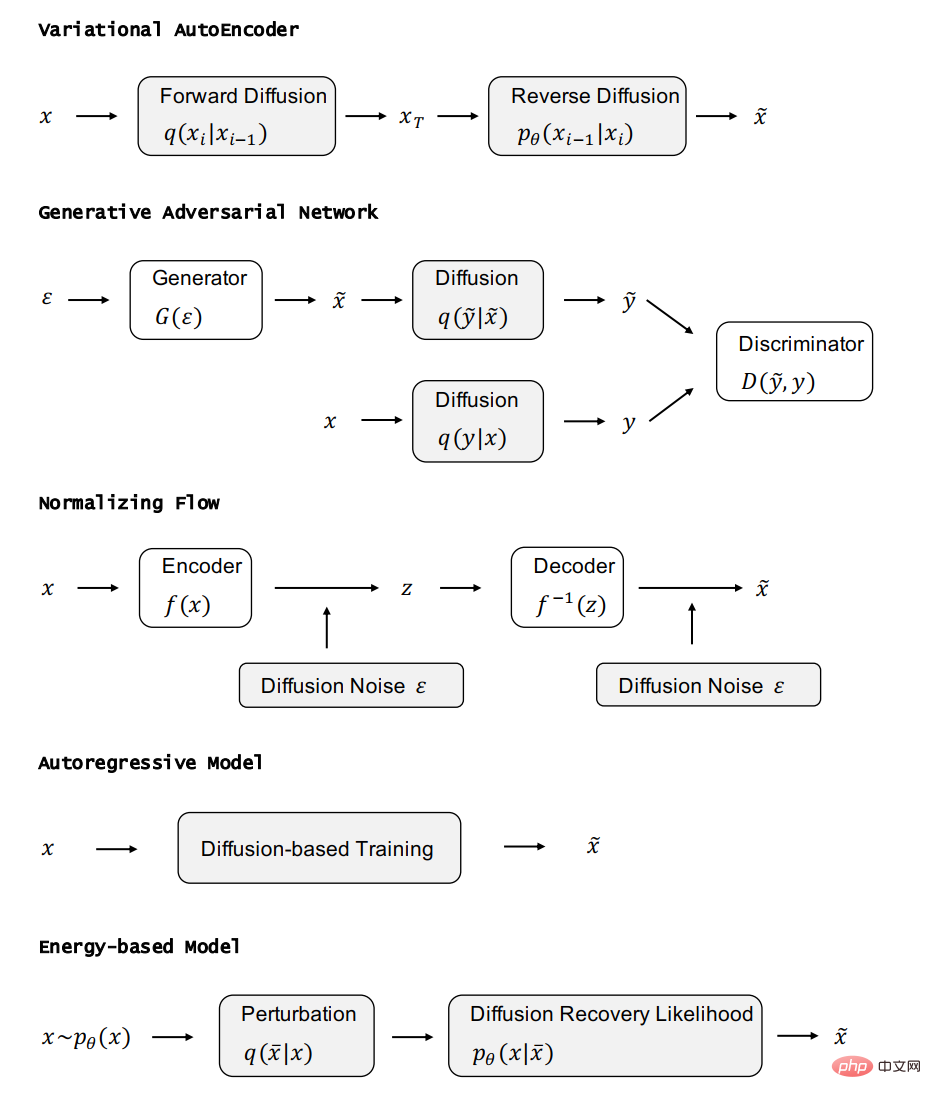
Dans cette section, nous introduisons l'application du modèle de diffusion en vision par ordinateur, traitement du langage naturel, traitement du signal de forme d'onde, apprentissage multimodal, génération de graphes moléculaires, séries chronologiques et confrontation Les applications dans sept domaines d'application majeurs tels que l'apprentissage, ainsi que les méthodes de chaque type d'application, sont subdivisées et analysées. Par exemple, en vision par ordinateur, le modèle de diffusion peut être utilisé pour la complétion et la réparation d'images (RePaint) :
Dans les tâches multimodales, le modèle de diffusion peut être utilisé pour la génération de texte en image (GLIDE ):

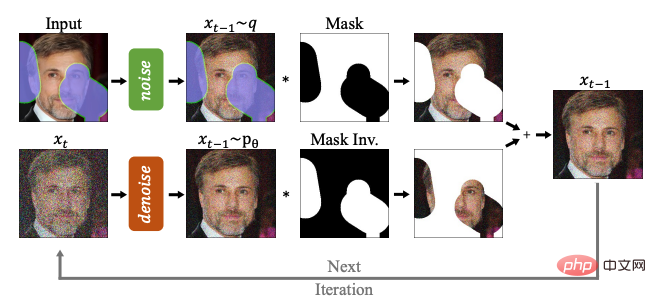
Vous pouvez également utiliser un modèle de diffusion pour générer des molécules de médicaments et des molécules de protéines (GeoDiff) dans la génération de graphes moléculaires :
Le résumé de la classification des applications est présenté dans le tableau :
8 Orientations futures de la recherche
- Re-test des hypothèses d'application. Nous devons examiner les hypothèses généralement acceptées que nous faisons dans nos applications. Par exemple, dans la pratique, on pense généralement que le processus direct du modèle de diffusion transformera les données en une distribution gaussienne standard, mais ce n'est pas le cas. Des étapes de diffusion plus avancées rendront la distribution finale de l'échantillon plus proche de la distribution gaussienne standard. distribution, cohérente avec le processus d'échantillonnage, mais des étapes de diffusion plus avancées rendent également l'estimation de la fonction fractionnaire plus difficile. Les conditions théoriques sont difficiles à obtenir, conduisant ainsi à un décalage entre la théorie et la pratique dans la pratique. Nous devons être conscients de cette situation et concevoir des modèles de diffusion appropriés.
- Du temps discret au temps continu. En raison de la flexibilité des modèles de diffusion, de nombreuses méthodes empiriques peuvent être améliorées par des analyses plus approfondies. Cette idée de recherche est prometteuse en convertissant des modèles à temps discret en modèles à temps continu correspondants, puis en concevant des méthodes discrètes plus nombreuses et de meilleure qualité.
- Processus nouvelle génération. Les modèles de diffusion génèrent des échantillons par deux méthodes principales : l'une consiste à discrétiser le SDE de diffusion inverse, puis à générer les échantillons via le SDE inverse discrétisé ; l'autre consiste à utiliser les propriétés de Markov du processus inverse pour débruiter progressivement les échantillons. Cependant, pour certaines tâches, il est difficile d’appliquer ces méthodes pour générer des échantillons en pratique. Par conséquent, des recherches plus approfondies sur de nouveaux processus et perspectives génératifs sont nécessaires.
- Généraliser à des scénarios plus complexes et à davantage de domaines de recherche. Bien que le modèle de diffusion ait été appliqué à de nombreux scénarios, la plupart d'entre eux sont limités à des scénarios à entrée et sortie uniques. À l'avenir, vous pourrez envisager de l'appliquer à des scénarios plus complexes, tels que la synthèse vocale texte-audiovisuel. Vous pouvez également envisager de le combiner avec davantage de domaines de recherche.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

