Maison >Périphériques technologiques >IA >Six algorithmes de clustering que les data scientists doivent connaître
Six algorithmes de clustering que les data scientists doivent connaître
- 王林avant
- 2023-04-08 23:31:022581parcourir
Actuellement, de nombreuses applications telles que Google Actualités utilisent des algorithmes de clustering comme principale méthode de mise en œuvre. Elles peuvent utiliser de grandes quantités de données non étiquetées pour créer un clustering de sujets puissant. Cet article présente 6 types de méthodes traditionnelles, du clustering K-means le plus basique aux méthodes puissantes basées sur la densité. Elles ont chacune leurs propres domaines d'expertise et scénarios, et les idées de base ne se limitent pas nécessairement aux méthodes de clustering.

Cet article commencera par un clustering K-means simple et efficace, puis présentera le clustering par décalage moyen, le clustering basé sur la densité, le clustering utilisant le mélange gaussien et les méthodes d'espérance maximale, le clustering hiérarchique et les méthodes adaptées au groupe de données structurées. détection. Nous analyserons non seulement les concepts de base de mise en œuvre, mais donnerons également les avantages et les inconvénients de chaque algorithme pour clarifier les scénarios d'application réels.
Le clustering est une technique d'apprentissage automatique qui consiste à regrouper des points de données. Étant donné un ensemble de points de données, nous pouvons utiliser un algorithme de clustering pour classer chaque point de données dans un groupe spécifique. En théorie, les points de données appartenant au même groupe devraient avoir des propriétés et/ou des caractéristiques similaires, tandis que les points de données appartenant à des groupes différents devraient avoir des propriétés et/ou des caractéristiques très différentes. Le clustering est une méthode d'apprentissage non supervisée et une technique d'analyse de données statistiques couramment utilisée dans de nombreux domaines.
K-Means (K-Means) Clustering
K-Means est probablement l'algorithme de clustering le plus connu. Il fait partie de nombreux cours d’introduction à la science des données et à l’apprentissage automatique. Très facile à comprendre et à implémenter dans le code ! Veuillez voir l'image ci-dessous.
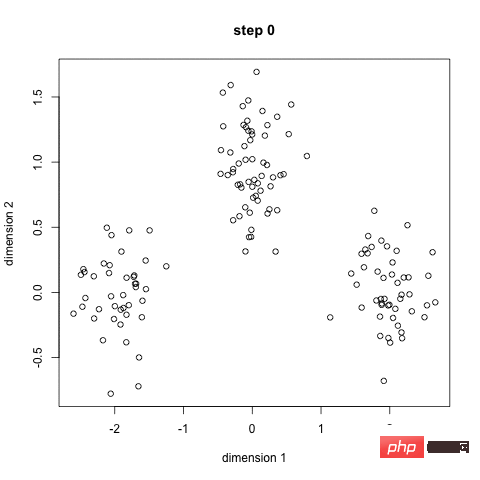
K-Means Clustering
Tout d'abord, nous sélectionnons quelques classes/groupes et initialisons au hasard leurs points centraux respectifs. Afin de déterminer le nombre de classes à utiliser, il est judicieux de jeter un coup d'œil rapide aux données et d'essayer d'identifier les différents groupes. Le point central est l'emplacement de même longueur que chaque vecteur de points de données, qui est « X » dans l'image ci-dessus.
Classez chaque point en calculant la distance entre le point de données et le centre de chaque groupe, puis classez le point dans le groupe dont le centre du groupe est le plus proche.
Sur la base de ces points de classement, nous utilisons la moyenne de tous les vecteurs du groupe pour recalculer le centre du groupe.
Répétez ces étapes pendant un certain nombre d'itérations, ou jusqu'à ce que le centre du groupe change peu après chaque itération. Vous pouvez également choisir d'initialiser le centre de groupe plusieurs fois de manière aléatoire, puis de choisir l'exécution qui semble fournir les meilleurs résultats.
K-Means a l'avantage d'être rapide, puisque nous ne faisons en réalité que calculer la distance entre le point et le centre du groupe : très peu de calcul ! Il a donc une complexité linéaire O(n).
D'un autre côté, K-Means présente certains inconvénients. Tout d’abord, vous devez choisir le nombre de groupes/classes. Cela n'est pas toujours fait avec soin et, idéalement, nous souhaitons que l'algorithme de clustering nous aide à résoudre le problème du nombre de classes à classer, car son objectif est d'obtenir des informations à partir des données. K-means part également de centres de cluster sélectionnés au hasard, de sorte qu'il peut produire différents résultats de clustering dans différents algorithmes. Par conséquent, les résultats peuvent ne pas être reproductibles et manquer de cohérence. D'autres méthodes de regroupement sont plus cohérentes.
K-Medians est un autre algorithme de clustering lié aux K-Means, sauf qu'au lieu d'utiliser la moyenne, les centres de groupe sont recalculés en utilisant le vecteur médian du groupe. Cette méthode est moins sensible aux valeurs aberrantes (car la médiane est utilisée), mais est beaucoup plus lente pour les ensembles de données plus volumineux car un tri est requis à chaque itération lors du calcul du vecteur médian.
Mean Shift Clustering
Mean Shift Clustering est un algorithme basé sur une fenêtre glissante qui tente de trouver des zones denses de points de données. Il s'agit d'un algorithme basé sur le centroïde, ce qui signifie que son objectif est de localiser le point central de chaque groupe/classe, ce qui est accompli en mettant à jour les points candidats du point central par rapport à la moyenne des points dans la fenêtre glissante. Ces fenêtres candidates sont ensuite filtrées lors d'une étape de post-traitement pour éliminer les quasi-duplications, formant ainsi l'ensemble final de points centraux et leurs groupes correspondants. Veuillez consulter la légende ci-dessous.

Regroupement à décalage moyen pour une seule fenêtre glissante
- Pour expliquer le décalage moyen, nous considérerons un ensemble de points dans un espace bidimensionnel comme le montre la figure ci-dessus. On part d'une fenêtre coulissante circulaire centrée au point C (choisi aléatoirement) et avec un noyau de rayon r. Le décalage moyen est un algorithme d'escalade qui implique de se déplacer de manière itérative vers des régions de densité plus élevée à chaque étape jusqu'à la convergence.
- À chaque itération, la fenêtre coulissante se déplace vers des zones de densité plus élevée en déplaçant le point central vers la moyenne des points à l'intérieur de la fenêtre (d'où le nom). La densité à l'intérieur d'une fenêtre glissante est proportionnelle au nombre de points à l'intérieur. Naturellement, en se déplaçant vers la moyenne des points à l'intérieur de la fenêtre, elle se déplace progressivement vers des zones de densité de points plus élevée.
- Nous continuons à déplacer la fenêtre glissante en fonction de la moyenne jusqu'à ce qu'il n'y ait plus de direction pouvant accueillir plus de points dans le noyau. Regardez l'image ci-dessus ; nous continuons à déplacer le cercle jusqu'à ce que la densité n'augmente plus (c'est-à-dire le nombre de points dans la fenêtre).
- Le processus des étapes 1 à 3 est complété par de nombreuses fenêtres coulissantes jusqu'à ce que tous les points soient situés dans une seule fenêtre. Lorsque plusieurs fenêtres coulissantes se chevauchent, la fenêtre contenant le plus de points est conservée. Ensuite, le clustering est effectué en fonction de la fenêtre glissante où se trouvent les points de données.
L'ensemble du processus du début à la fin pour toutes les fenêtres coulissantes est présenté ci-dessous. Chaque point noir représente le centre de gravité de la fenêtre glissante et chaque point gris représente un point de données.

L'ensemble du processus de clustering par décalage moyen
Par rapport au clustering K-means, cette méthode ne nécessite pas la sélection du nombre de clusters car le décalage moyen le découvre automatiquement. C'est un énorme avantage. Le fait que le cluster centre le cluster vers la densité de points maximale est également très satisfaisant, car il est très intuitif de comprendre et de s'adapter à la signification naturelle basée sur les données. L'inconvénient est que le choix de la taille de la fenêtre/du rayon « r » peut être sans importance.
Méthode de clustering basée sur la densité (DBSCAN)
DBSCAN est un algorithme de clustering basé sur la densité qui est similaire au décalage moyen mais présente des avantages significatifs. Découvrez un autre graphique amusant ci-dessous et commençons !
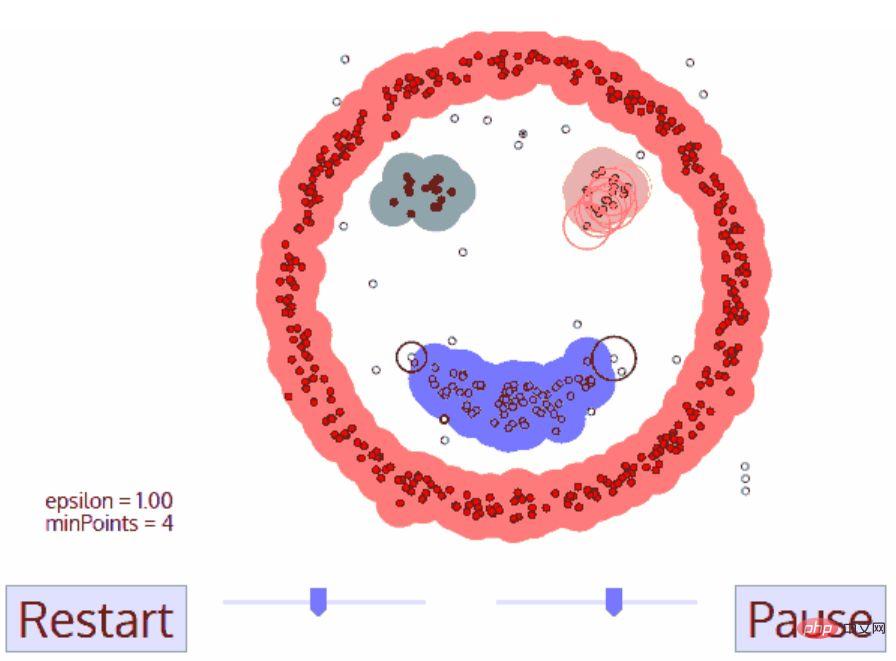
DBSCAN Clustering
- DBSCAN démarre à partir d'un point de données de départ arbitraire qui n'a pas été visité. Le voisinage de ce point est extrait avec une distance ε (tous les points à une distance ε sont des points voisins).
- S'il y a un nombre suffisant de points dans ce quartier (selon minPoints), le processus de clustering démarre et le point de données actuel devient le premier point du nouveau cluster. Sinon, le point sera marqué comme bruit (plus tard, ce point de bruit pourra encore faire partie du cluster). Dans les deux cas, le point est marqué comme « Visité ».
- Pour le premier point d'un nouveau cluster, les points situés dans son voisinage de distance ε deviennent également partie du cluster. Ce processus consistant à faire en sorte que tous les points du voisinage ε appartiennent au même cluster est répété pour tous les nouveaux points qui viennent d'être ajoutés au cluster.
- Répétez les étapes 2 et 3 jusqu'à ce que tous les points du cluster soient déterminés, c'est-à-dire que tous les points du voisinage ε du cluster aient été visités et marqués.
- Une fois que nous en aurons terminé avec le cluster actuel, un nouveau point non visité sera récupéré et traité, entraînant la découverte d'un autre cluster ou bruit. Ce processus est répété jusqu'à ce que tous les points soient marqués comme visités. Puisque tous les points ont été visités, chaque point appartient à un cluster ou à un bruit.
DBSCAN présente de nombreux avantages par rapport aux autres algorithmes de clustering. Premièrement, cela ne nécessite pas du tout un nombre fixe de clusters. Il identifie également les valeurs aberrantes comme du bruit, contrairement au décalage moyen, qui regroupe simplement les points de données en clusters même s'ils sont très différents. De plus, il est capable de trouver très bien des clusters de n’importe quelle taille et forme.
Le principal inconvénient de DBSCAN est qu'il ne fonctionne pas aussi bien que les autres algorithmes de clustering lorsque la densité des clusters est différente. En effet, les paramètres du seuil de distance ε et des minPoints utilisés pour identifier les points de voisinage changeront avec les clusters lorsque la densité change. Cet inconvénient se pose également dans les données de très grande dimension, car le seuil de distance ε devient là encore difficile à estimer.
Clustering d'espérance maximale (EM) avec des modèles de mélange gaussiens (GMM)
Un inconvénient majeur des K-Means est sa simple utilisation des moyennes centrales de cluster. Le diagramme ci-dessous nous montre pourquoi ce n’est pas la meilleure approche. A gauche, on voit très clairement qu'il existe deux amas circulaires de rayons différents, centrés sur la même moyenne. Les K-Means ne peuvent pas gérer cette situation car les moyennes de ces clusters sont très proches. K-Means échoue également dans les cas où les clusters ne sont pas circulaires, encore une fois en raison de l'utilisation de la moyenne comme centre du cluster.

Deux cas d'échec des K-Means
Les modèles de mélange gaussien (GMM) nous offrent plus de flexibilité que les K-Means. Pour les GMM, nous supposons que les points de données sont distribués de manière gaussienne ; il s'agit d'une hypothèse moins restrictive que l'utilisation de la moyenne pour supposer qu'ils sont circulaires. De cette façon, nous disposons de deux paramètres pour décrire la forme du cluster : la moyenne et l’écart type ! En prenant la 2D comme exemple, cela signifie que les clusters peuvent prendre n'importe quel type de forme elliptique (puisque nous avons des écarts types dans les directions x et y). Par conséquent, chaque distribution gaussienne est affectée à un seul cluster.
Pour trouver les paramètres gaussiens (tels que la moyenne et l'écart type) de chaque cluster, nous utiliserons un algorithme d'optimisation appelé Expectation Maximum (EM). Regardez le diagramme ci-dessous, qui est un exemple d'ajustement gaussien à un cluster. Nous pouvons ensuite poursuivre le processus de clustering à attentes maximales à l'aide de GMM.
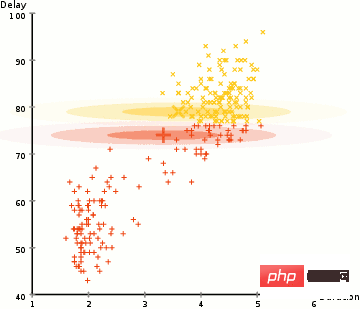
EM Clustering à l'aide de GMM
- Nous choisissons d'abord le nombre de clusters (comme avec les K-Means) et initialisons aléatoirement les paramètres de distribution gaussienne pour chaque cluster. Vous pouvez également essayer de fournir une bonne estimation des paramètres initiaux en jetant un coup d’œil rapide aux données. Notez cependant que comme vous pouvez le voir ci-dessus, cela n'est pas nécessaire à 100% car la gaussienne démarre très mal mais s'optimise rapidement.
- Étant donné la distribution gaussienne de chaque cluster, calculez la probabilité que chaque point de données appartienne à un cluster spécifique. Plus un point est proche du centre de la gaussienne, plus il a de chances d’appartenir à ce cluster. Cela devrait être intuitif puisqu'avec une distribution gaussienne, nous supposons que la plupart des données sont plus proches du centre du cluster.
- Sur la base de ces probabilités, nous calculons un nouvel ensemble de paramètres de distribution gaussienne qui maximisent la probabilité des points de données au sein du cluster. Nous calculons ces nouveaux paramètres en utilisant une somme pondérée des emplacements des points de données, où le poids est la probabilité que le point de données appartienne à ce cluster particulier. Pour l'expliquer visuellement, nous pouvons jeter un œil à l'image ci-dessus, notamment le cluster jaune, que nous utilisons comme exemple. La distribution démarre immédiatement dès la première itération, mais on peut voir que la plupart des points jaunes se trouvent du côté droit de la distribution. Lorsque nous calculons une somme pondérée par probabilité, même s’il y a certains points proches du centre, ils se trouvent principalement du côté droit. La moyenne de la distribution sera donc naturellement proche de ces points. On constate également que la plupart des points sont répartis « du haut à droite vers le bas à gauche ». L'écart type est donc modifié pour créer une ellipse qui s'ajuste mieux aux points afin de maximiser la somme pondérée des probabilités.
- Répétez les étapes 2 et 3 jusqu'à convergence, où la distribution change peu entre les itérations.
L'utilisation des GMM présente deux avantages clés. Premièrement, les GMM sont plus flexibles que les K-Means en termes de covariance de cluster en raison du paramètre d'écart type, les clusters peuvent prendre n'importe quelle forme elliptique au lieu d'être limités à des cercles. K-Means est en fait un cas particulier de GMM, où la covariance de chaque cluster est proche de 0 dans toutes les dimensions. Deuxièmement, comme les GMM utilisent des probabilités, il peut y avoir de nombreux clusters par point de données. Ainsi, si un point de données se trouve au milieu de deux clusters qui se chevauchent, nous pouvons définir sa classe simplement en disant que X pour cent appartient à la classe 1 et Y pour cent à la classe 2. Autrement dit, les GMM prennent en charge les qualifications hybrides.
Clustering hiérarchique aggloméré
Les algorithmes de clustering hiérarchique sont en fait divisés en deux catégories : descendant ou ascendant. Les algorithmes ascendants traitent d'abord chaque point de données comme un seul cluster, puis fusionnent (ou agrégent) deux clusters successivement jusqu'à ce que tous les clusters soient fusionnés en un seul cluster contenant tous les points de données. Par conséquent, le clustering hiérarchique ascendant est appelé clustering hiérarchique agglomératif ou HAC. Cette hiérarchie de clusters est représentée par un arbre (ou dendrogramme). La racine de l’arbre est la seule grappe qui collecte tous les échantillons, et les feuilles sont les grappes ne contenant qu’un seul échantillon. Avant d'entrer dans les étapes de l'algorithme, veuillez consulter la légende ci-dessous.
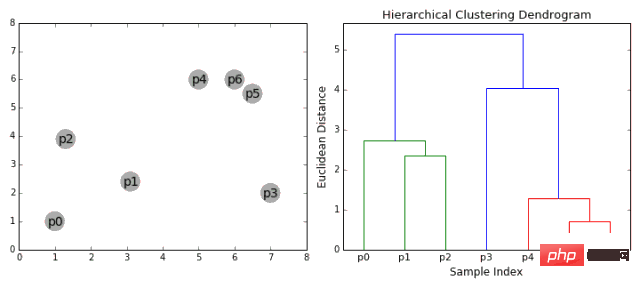
Clustering hiérarchique aggloméré
- Nous traitons d'abord chaque point de données comme un cluster unique, c'est-à-dire que si nous avons X points de données dans notre ensemble de données, alors nous avons X clusters. Nous choisissons ensuite une métrique de distance qui mesure la distance entre deux clusters. À titre d'exemple, nous utiliserons le lien moyen, qui définit la distance entre deux clusters comme la distance moyenne entre les points de données du premier cluster et les points de données du deuxième cluster.
- À chaque itération, nous fusionnons deux clusters en un seul. Les deux clusters à fusionner devraient avoir le lien moyen le plus petit. Autrement dit, selon la métrique de distance que nous choisissons, les deux clusters ont la plus petite distance entre eux et sont donc les plus similaires et doivent être fusionnés.
- Répétez l'étape 2 jusqu'à ce que nous atteignions la racine de l'arbre, c'est-à-dire que nous n'avons qu'un seul cluster contenant tous les points de données. De cette façon, il nous suffit de choisir quand arrêter de fusionner les clusters, c'est-à-dire quand arrêter de construire l'arborescence, pour choisir le nombre de clusters dont nous avons besoin au final !
Le clustering hiérarchique ne nous oblige pas à spécifier le nombre de clusters, nous pouvons même choisir quel nombre de clusters nous convient le mieux puisque nous construisons un arbre. De plus, l’algorithme n’est pas sensible au choix de la métrique de distance ; ils fonctionnent tous aussi bien, alors que pour d’autres algorithmes de clustering, le choix de la métrique de distance est crucial. Un exemple particulièrement intéressant de méthodes de clustering hiérarchique est celui où les données sous-jacentes ont une structure hiérarchique et que vous souhaitez restaurer la hiérarchie ; Contrairement à la complexité linéaire des K-Means et du GMM, ces avantages du clustering hiérarchique se font au prix d'une efficacité moindre car il a une complexité temporelle de O(n³).
Détection de communauté graphique
Lorsque nos données peuvent être représentées sous forme de réseau ou de graphique, nous pouvons utiliser la méthode de détection de communauté graphique pour terminer le clustering. Dans cet algorithme, une communauté de graphes est généralement définie comme un sous-ensemble de sommets plus étroitement connectés que les autres parties du réseau.
Le cas le plus intuitif est peut-être celui des réseaux sociaux. Les sommets représentent des personnes et les arêtes reliant les sommets représentent des utilisateurs amis ou fans. Cependant, pour modéliser un système sous forme de réseau, nous devons trouver un moyen de connecter efficacement les différents composants. Certaines applications innovantes de la théorie des graphes pour le clustering incluent l'extraction de caractéristiques des données d'image, l'analyse des réseaux de régulation génétique, etc.
Vous trouverez ci-dessous un diagramme simple montrant 8 sites Web récemment consultés, connectés en fonction des liens de leurs pages Wikipédia.
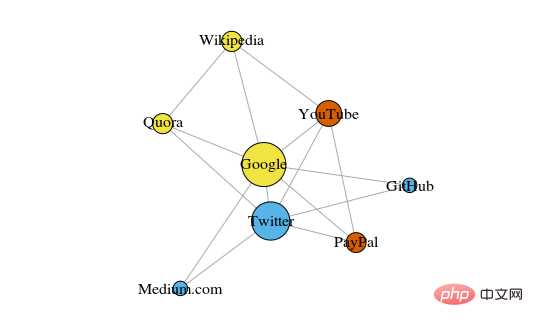
La couleur de ces sommets indique leur relation de groupe, et la taille est déterminée en fonction de leur centralité. Ces clusters ont également un sens dans la vie réelle, où les sommets jaunes sont généralement des sites de référence/de recherche et les sommets bleus sont tous des sites de publication en ligne (articles, tweets ou codes).
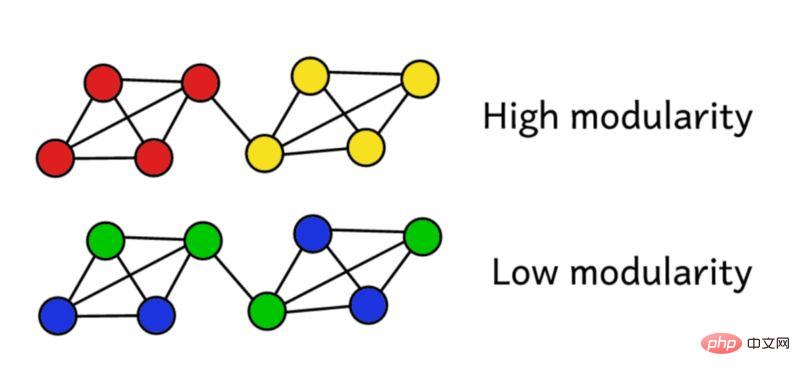
Supposons que nous ayons regroupé le réseau en groupes. Nous pouvons ensuite utiliser ce score de modularité pour évaluer la qualité du clustering. Un score plus élevé signifie que nous avons segmenté le réseau en groupes « précis », tandis qu'un score faible signifie que notre regroupement est plus proche du hasard. Comme le montre la figure ci-dessous :
La modularité peut être calculée à l'aide de la formule suivante :
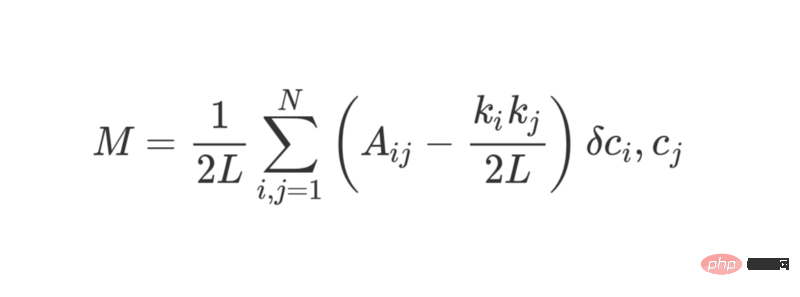
où L représente le nombre d'arêtes du réseau, k_i et k_j font référence au degré de chaque sommet, qui peut être calculé en additionnant chaque ligne. Il est obtenu en additionnant les éléments de chaque colonne. Multiplier les deux et diviser par 2L représente le nombre attendu d'arêtes entre les sommets i et j lorsque le réseau est attribué aléatoirement.
Dans l'ensemble, les termes entre parenthèses représentent la différence entre la véritable structure du réseau et la structure attendue lorsqu'ils sont combinés aléatoirement. L'étude de sa valeur montre qu'elle renvoie la valeur la plus élevée lorsque A_ij = 1 et ( k_i k_j ) / 2L est petit. Cela signifie que lorsqu'il y a une arête « inattendue » entre les points fixes i et j, la valeur résultante est plus élevée.
Le dernier δc_i, c_j est la fameuse fonction Kronecker δ (fonction Kronecker-delta). Voici son explication Python :

La modularité du graphique peut être calculée à l'aide de la formule ci-dessus, et plus la modularité est élevée, meilleur est le degré de regroupement du réseau en différents groupes. Par conséquent, la meilleure façon de regrouper le réseau peut être trouvée en recherchant une modularité maximale grâce à des méthodes d’optimisation.
La combinatoire nous dit que pour un réseau avec seulement 8 sommets, il existe 4140 méthodes de clustering différentes. Un réseau de 16 sommets serait regroupé de plus de 10 milliards de façons. Les méthodes de clustering possibles d'un réseau à 32 sommets dépasseront 128 septillions (10^21) ; si votre réseau comporte 80 sommets, le nombre de méthodes de clustering possibles a dépassé le nombre de méthodes de clustering dans l'univers observable.
Nous devons donc recourir à une heuristique qui fonctionne bien pour évaluer les clusters qui donnent les scores de modularité les plus élevés, sans essayer toutes les possibilités. Il s'agit d'un algorithme appelé Fast-Greedy Modularity-Maximization, qui est quelque peu similaire à l'algorithme de clustering hiérarchique agglomératif décrit ci-dessus. C'est juste que Mod-Max ne fusionne pas des groupes en fonction de la distance, mais fusionne des groupes en fonction des changements de modularité.
Voici comment cela fonctionne :
- Attribuez d'abord chaque sommet à son propre groupe, puis calculez la modularité M de l'ensemble du réseau.
- L'étape 1 nécessite que chaque paire de communautés soit liée par au moins un lien unilatéral. Si deux communautés fusionnent, l'algorithme calcule le changement de modularité résultant ΔM.
- L'étape 2 consiste à sélectionner les paires de groupes avec la plus grande croissance en ΔM, puis à les fusionner. Une nouvelle modularité M est alors calculée pour ce cluster et enregistrée.
- Répétez les étapes 1 et 2 - à chaque fois en fusionnant les paires de groupes de telle sorte que vous obteniez le gain maximum de ΔM, puis enregistrez le nouveau modèle de clustering et son score de modularité correspondant M.
- Vous pouvez vous arrêter lorsque tous les sommets sont regroupés dans un cluster géant. L'algorithme examine ensuite les enregistrements au cours de ce processus et trouve le modèle de regroupement dans lequel la valeur M la plus élevée a été renvoyée. Il s'agit de la structure de groupe renvoyée.
La détection de communauté est un domaine de recherche populaire en théorie des graphes. Ses limites se reflètent principalement dans le fait qu'elle ignore certains petits clusters et n'est applicable qu'aux modèles de graphes structurés. Mais ce type d'algorithme a de très bonnes performances dans les données structurées typiques et les données de réseau réelles.
Conclusion
Voici les 6 principaux algorithmes de clustering que les data scientists devraient connaître ! Nous terminerons cet article en montrant des visualisations de divers algorithmes !
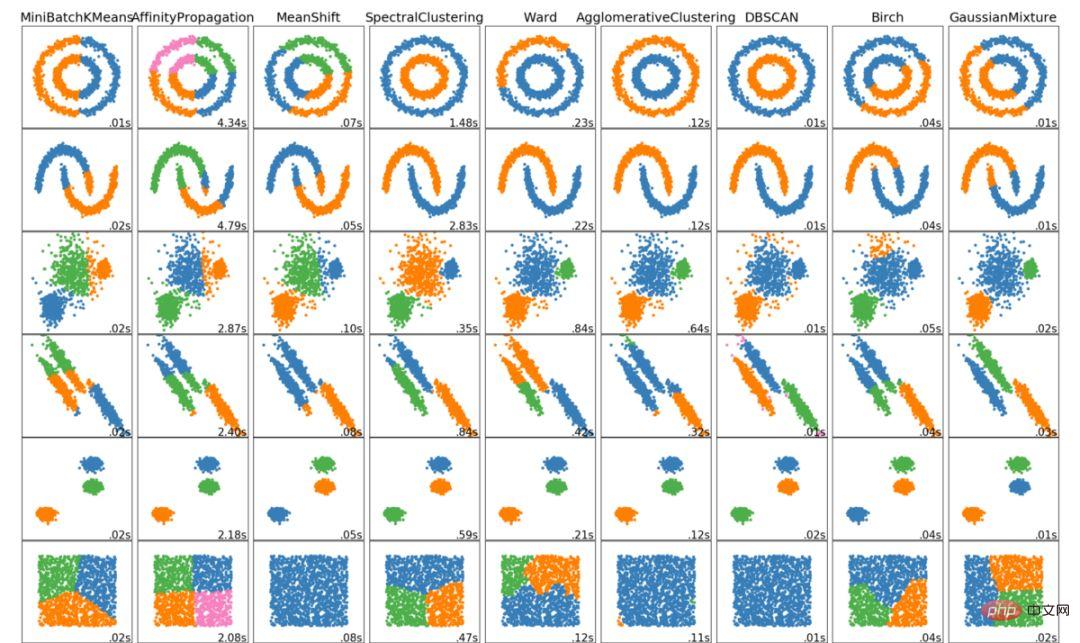
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

