Maison >Périphériques technologiques >IA >L'équation est-elle une forêt d'arbres binaires ? Découvrez des équations dirigeantes et des mécanismes physiques inconnus directement à partir des données
L'équation est-elle une forêt d'arbres binaires ? Découvrez des équations dirigeantes et des mécanismes physiques inconnus directement à partir des données
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-08 18:11:041151parcourir
Les chercheurs espèrent utiliser des méthodes d'apprentissage automatique pour extraire automatiquement les lois intrinsèques les plus précieuses et les plus importantes directement à partir de données non linéaires de haute dimension (c'est-à-dire pour exploiter les équations régissant le problème basées sur l'EDP) afin de parvenir à une découverte automatique des connaissances.
Récemment, des équipes de recherche de l'Eastern Institute of Technology, de l'Université de Washington, de Ruilai Intelligence, de l'Université de Pékin et d'autres institutions ont proposé un algorithme génétique SGA-PDE basé sur les mathématiques symboliques, construisant un ensemble de candidats ouverts qui peut directement extraire n'importe quelle forme du équation de contrôle des données.
Les expériences montrent que SGA-PDE peut non seulement exploiter l'équation de Burgers (avec termes d'interaction), l'équation de Korteweg – de Vries (KdV, avec termes dérivés d'ordre supérieur) et l'équation de Chafee-Infante (avec termes exponentiels et dérivés termes) à partir des données ), et a également exploré avec succès les équations gouvernantes avec des fonctions composites et des équations avec des structures fractionnaires dans le problème de l'écoulement visqueux par gravité, dont les deux dernières étaient difficiles à découvrir avec les méthodes précédentes. SGA-PDE ne s'appuie pas sur des connaissances préalables sur la forme de l'équation et comble le vide dans les problèmes complexes d'exploration d'équations de contrôle de structure. Ce modèle ne nécessite pas qu'un ensemble d'équations candidates soit donné à l'avance, ce qui est bénéfique pour l'application pratique d'algorithmes de découverte automatique de connaissances dans des problèmes scientifiques inconnus.
L'étude, intitulée "Algorithme génétique symbolique pour la découverte d'équations aux dérivées partielles de forme ouverte (SGA-PDE)", a été publiée dans Physical Review Research le 1er juin.

L'idée commune actuelle de découverte des connaissances est d'utiliser la régression clairsemée, c'est-à-dire qu'un ensemble candidat fermé est donné à l'avance, puis les termes de l'équation en sont sélectionnés et les équations gouvernantes sont combinées, telles que SINDy et PDE- TROUVER. Cependant, ce type de méthode nécessite que l'utilisateur détermine à l'avance la forme approximative de l'équation, puis fournisse à l'avance tous les opérateurs différentiels correspondants comme termes de fonction dans l'ensemble candidat. Les termes de fonction qui n'existent pas dans l'ensemble candidat ne peuvent pas être trouvés. à partir des données. Certaines des recherches les plus récentes tentent d'utiliser des algorithmes génétiques pour élargir les ensembles de candidats, mais il existe des limites majeures en matière de recombinaison et de mutation génétiques, et il est toujours impossible de générer des termes de fonction structurelle complexes (tels que des structures fractionnaires et des fonctions composites) directement à partir des données. La clé des équations de gouvernance de forme ouverte est de générer et de représenter des formes arbitraires d'équations de gouvernance d'une manière facile à calculer, et d'évaluer l'exactitude de la forme de l'équation en mesurant dans quelle mesure les équations générées s'ajustent aux données observées. puis effectuez des expériences sur les équations extraites. Optimisation itérative. Par conséquent, les problèmes fondamentaux de la découverte automatique des connaissances sont la représentation et l’optimisation.
Tableau 1. Tableau de comparaison des méthodes d'extraction d'équations de contrôle automatique
 Le défi de la représentation du problème est :
Le défi de la représentation du problème est :
; 2. Comment construire une représentation d’équation de contrôle facile à calculer. Afin de pouvoir exprimer librement des équations de n'importe quelle structure, les chercheurs ont réduit l'unité de représentation de base de SGA-PDE aux opérandes et aux opérateurs, et ont utilisé des arbres binaires pour construire un ensemble de candidats ouverts grâce aux mathématiques symboliques.
Les défis du problème d'optimisation sont : 1. Le gradient entre la forme de l'équation et l'indice d'évaluation de l'équation est difficile à calculer 2 Le domaine réalisable de l'ensemble candidat ouvert est infini, et il est difficile pour le problème d'optimisation. processus d'optimisation pour équilibrer efficacement l'exploration et l'utilisation (exploitation). Afin d’optimiser efficacement le problème de l’ensemble candidat ouvert, les chercheurs ont utilisé un algorithme génétique spécialement conçu pour les structures arborescentes afin de réaliser une optimisation sous forme d’équations.
Figure 1 : Diagramme schématique du problème de découverte automatique des connaissances et SGA-PDE
Les chercheurs ont d'abord représenté l'équation différentielle partielle de forme ouverte en affinant l'unité de représentation de base de l'équation dans l'algorithme,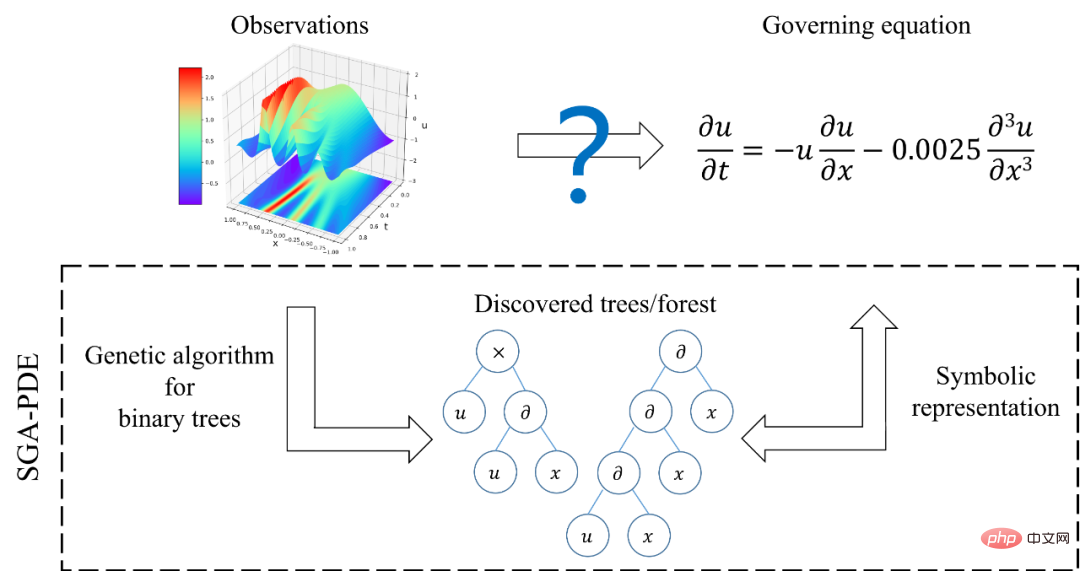 a modifié la l'échelle de représentation de l'équation du niveau de terme de fonction indépendante est transformée en un niveau d'opérateur et d'opérande plus basique
a modifié la l'échelle de représentation de l'équation du niveau de terme de fonction indépendante est transformée en un niveau d'opérateur et d'opérande plus basique
SGA-PDE divise les opérateurs de l'équation de contrôle en opérateurs doubles (tels que +, -) et opérateurs simples (tels que sin, cos), puis définit toutes les variables potentielles sous forme d'opérandes (tels que x, t, u). Les chercheurs utilisent la structure d’un arbre binaire pour combiner des opérateurs et des opérandes afin de coder différentes équations. Tous les nœuds terminaux (nœuds feuilles de degré 0) dans l'arbre binaire correspondent aux opérandes, et tous les nœuds non terminaux correspondent aux opérateurs. Les opérateurs doubles correspondent aux nœuds de degré 2 et les opérateurs simples correspondent aux nœuds de degré 1. .
Comme le montre la figure 2, grâce à une chaîne calculable comme connexion, n'importe quel terme de fonction peut être transformé en un arbre binaire En même temps, un arbre binaire qui satisfait certaines règles mathématiques peut également être transformé en fonction. terme. De plus, une équation gouvernante avec plusieurs termes de fonction équivaut à une forêt composée de plusieurs arbres binaires. SGA-PDE représente toute équation différentielle partielle de forme ouverte régissant les mathématiques symboliques. En outre, l'article propose également une méthode pour générer de manière aléatoire des arbres binaires ayant une signification mathématique, qui peut garantir que les arbres binaires générés ne violent pas les principes mathématiques.
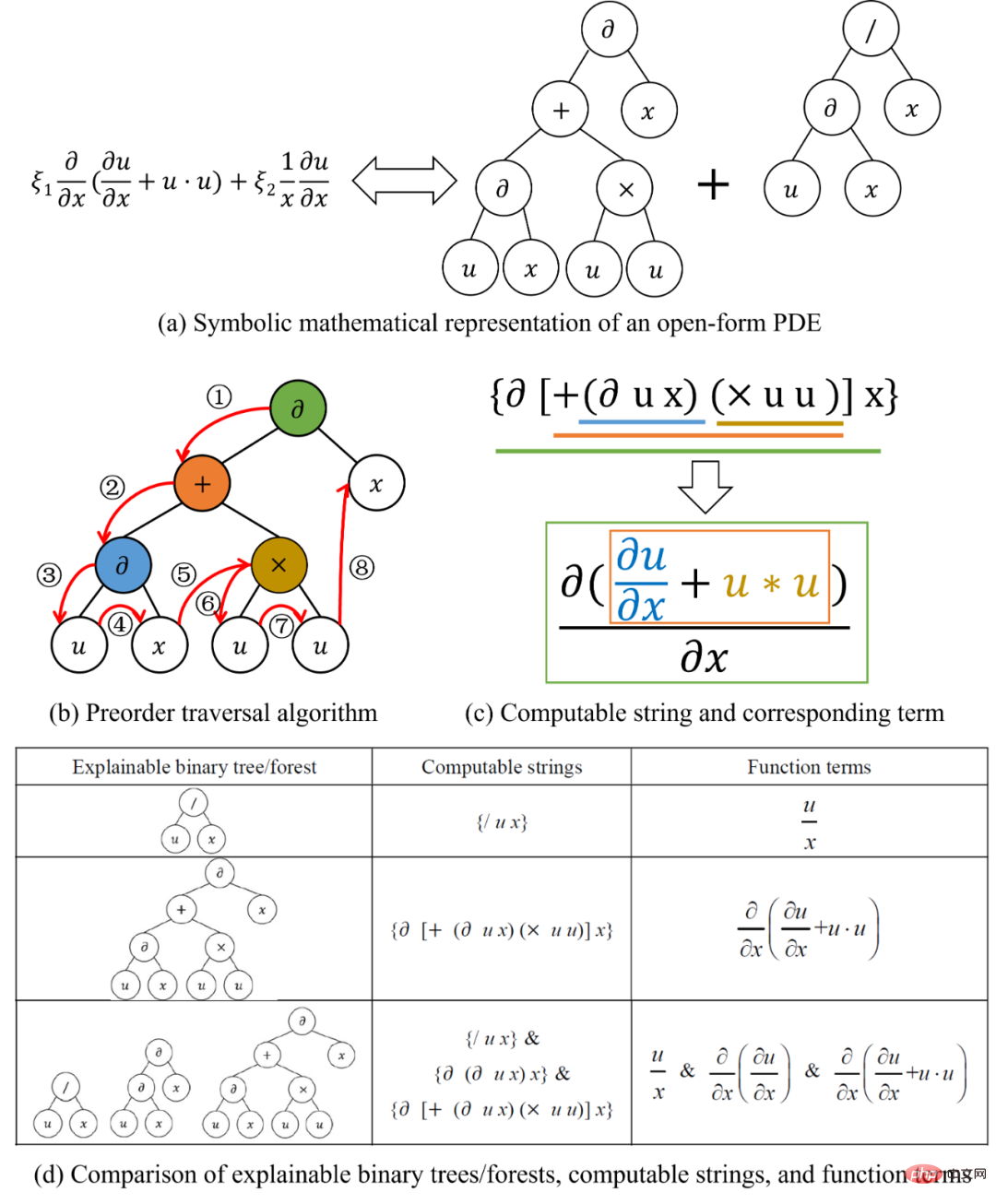
Figure 2 : Méthode de représentation et de transformation entre les arbres binaires et les termes de fonction
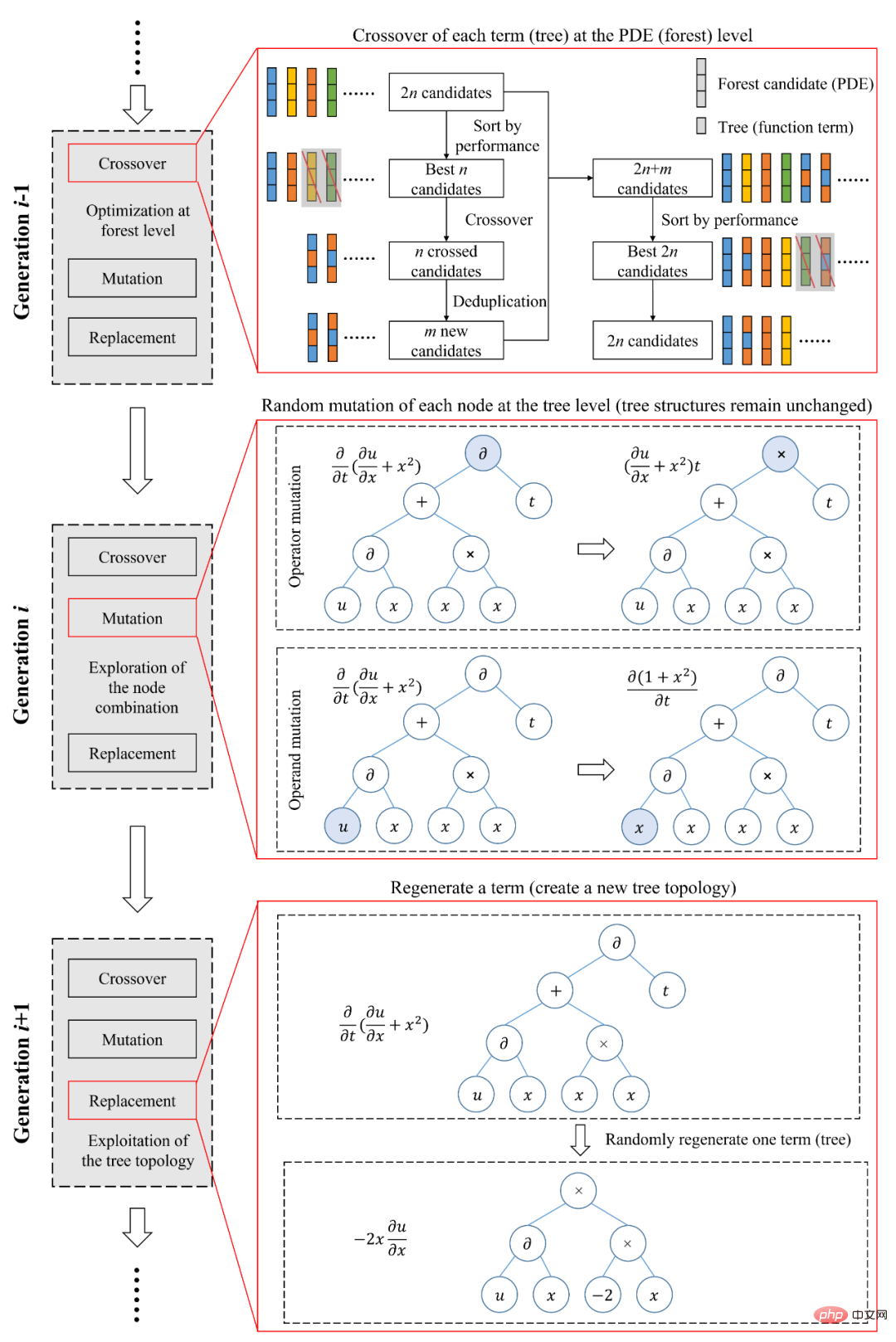
Parce que la méthode de représentation présentée dans la figure 2 peut correspondre de manière biunivoque entre les échantillons dans l'espace des fonctions et les échantillons dans l'espace de l'arbre binaire . Cela signifie que les représentations basées sur les mathématiques symboliques sont efficaces et non redondantes et peuvent être utilisées comme processus de codage dans les algorithmes génétiques. Les chercheurs ont proposé un algorithme génétique pour les structures arborescentes (Figure 3) pour extraire automatiquement des équations de contrôle cohérentes avec les données observées à partir de données expérimentales. Cet algorithme génétiquepour les structures arborescentes peut réaliser une optimisation à différents niveaux.
Le lien de réorganisation est optimiséau niveau de la forêt (équation) pour trouver la combinaison optimale d'arbres binaires (termes de fonction). Ce lien est similaire à la méthode de régression clairsemée courante actuelle, qui consiste en une optimisation au sein d'un ensemble candidat fermé.
Le lien de mutation est optimisé au niveau de l'arbre binaire (terme de fonction)En générant aléatoirement différents attributs de nœud, nous trouvons la combinaison optimale d'attributs de nœud sous une structure d'arbre binaire donnée. .
Le lien de remplacement est également optimisé au niveau de l'arbre binaire (terme de fonction), mais il générera une nouvelle structure d'arbre binaire, qui est une exploration de la structure arborescente et réalise l'optimisation d'un ensemble de candidats complètement ouverts. SGA-PDE peut prendre en compte l'utilisation et l'exploration de la topologie de l'arbre binaire grâce à une optimisation multi-niveaux, ce qui permet de trouver efficacement la forme d'équation optimale.
Les données expérimentales sont présentées dans la figure 4, où la colonne 2 montre les observations physiques sur le terrain,
est la seule information d'entrée dans SGA-PDE. Les dérivées premières sous-jacentes dans les colonnes 3 et 4 peuvent être obtenues en différenciant les observations physiques sur le terrain. La colonne 1 est la forme correcte de l'équation. Dans l'expérience, SGA-PDE utilise les mêmes opérandes et opérateurs prédéfinis et n'a pas besoin d'être ajusté à des problèmes spécifiques afin de vérifier la polyvalence de l'algorithme. Enfin, SGA-PDE a exploité avec succès l'équation de Burgers, l'équation de KdV, l'équation de Chafee-Infante, l'équation régissant l'écoulement gravitationnel visqueux avec dérivation de fonction composite et les équations à structure fractionnaire à partir des données. L'équation ci-dessus a de nombreuses formes complexes
telles que des termes exponentiels, des termes dérivés d'ordre supérieur, des termes d'interaction, des fonctions composites et des structures imbriquées.Le tableau 2 compare les résultats de calcul de divers algorithmes existants dans les cinq exemples de calcul ci-dessus. On peut voir que SGA-PDE comble le vide dans l'exploration des équations de contrôle de structures complexes
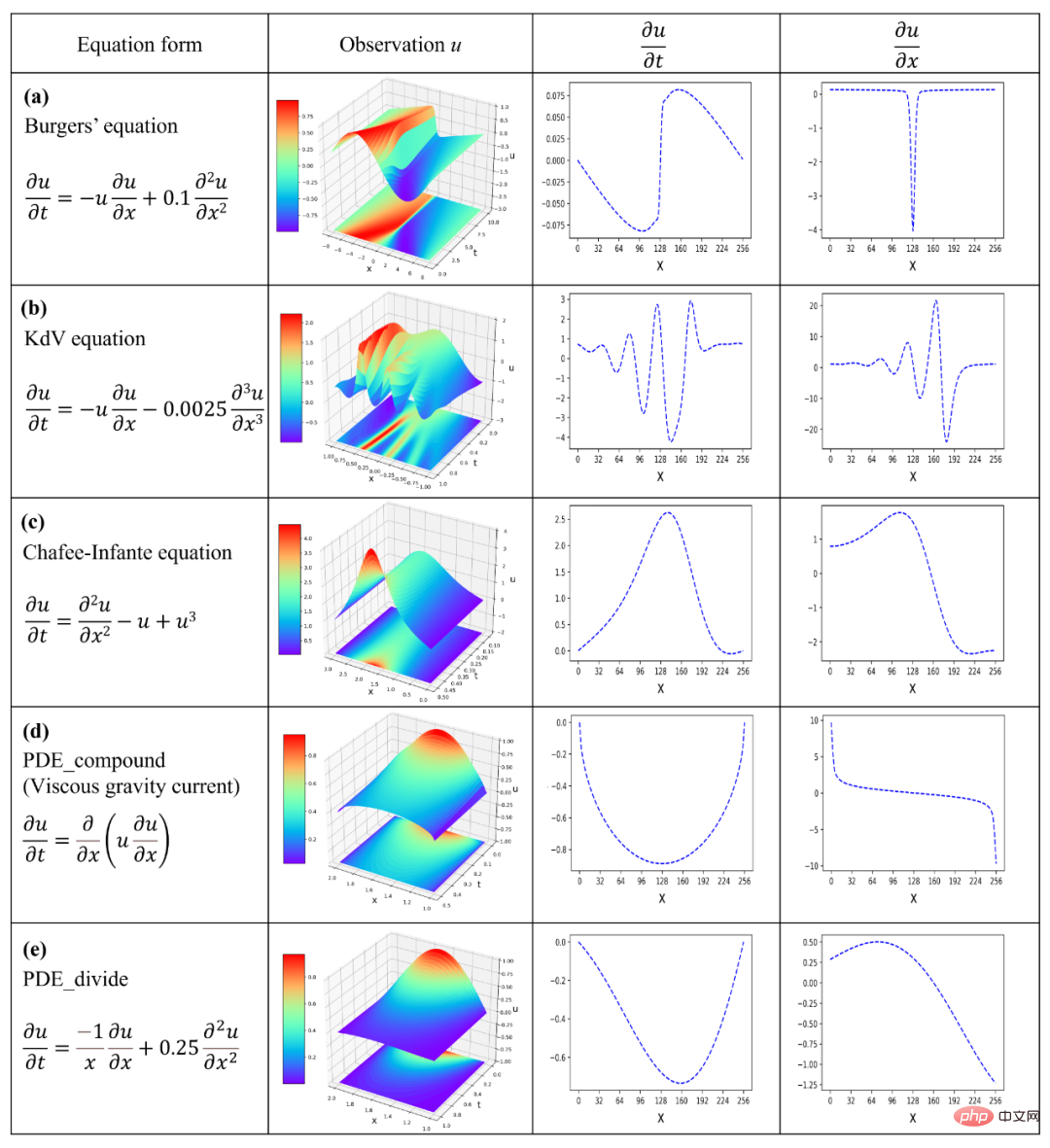 Figure 4 : Graphique de données expérimentales.
Figure 4 : Graphique de données expérimentales.

Tableau 2 Résultats expérimentaux de l'algorithme de découverte automatique des connaissances dans différents problèmes d'exploration d'équations de contrôle
Afin de mieux comprendre le processus d'optimisation de SGA-PDE, la figure 5 montre le chemin d'évolution lors de l'exploration de l'équation KdV. On constate que l’équation optimale générée par la première génération est loin de l’équation réelle. Dans le processus d'évolution ultérieur, avec les changements dans la structure topologique de l'arbre binaire et la signification des nœuds, ainsi que la recombinaison croisée entre les termes de fonction, la bonne solution a finalement été trouvée dans la 31ème génération, et à cette époque l'indice AIC a atteint la convergence donnée dans l'article standard. Il est intéressant de noter que si l’optimisation se poursuit, une expression plus parcimonieuse de l’équation KdV basée sur la dérivation d’une fonction composite se trouve à la génération 69. La figure 6 montre le processus d'optimisation de SGA-PDE pour trouver les équations gouvernantes à structure fractionnaire.
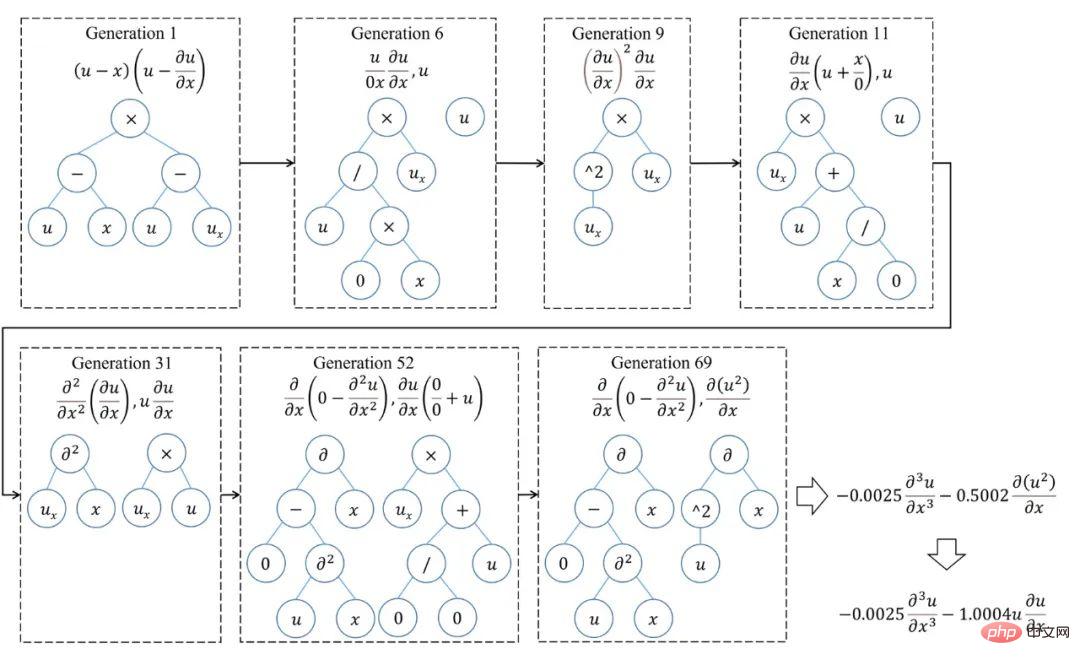
Figure 5 : Processus d'optimisation de SGA-PDE pour l'équation KdV
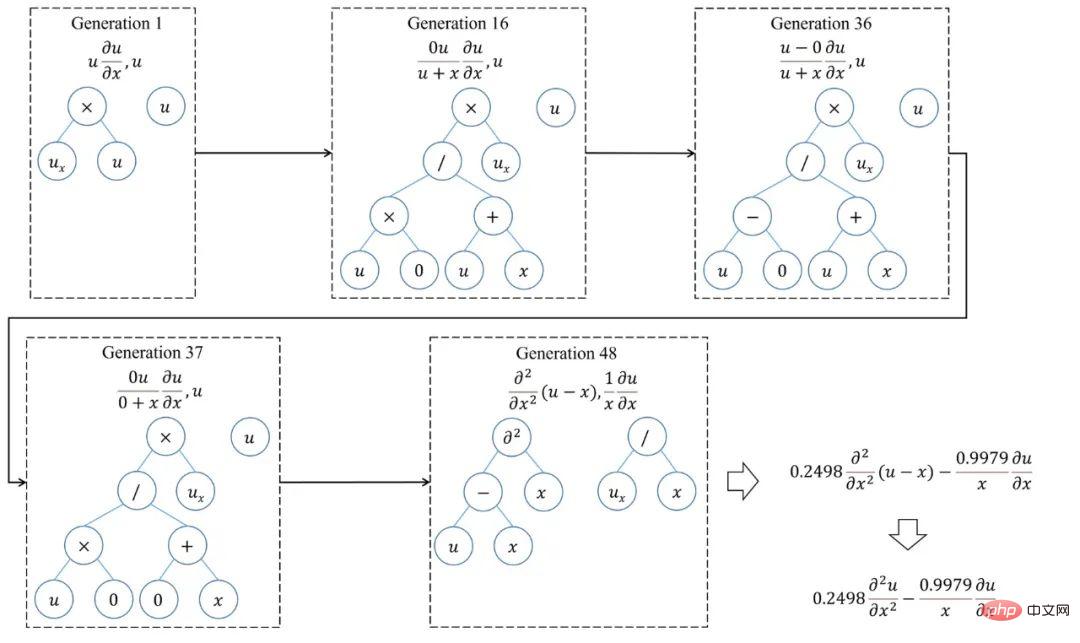
Figure 6 : Processus d'optimisation de SGA-PDE pour les équations à structure fractionnaire
Les équations de contrôle sont des connaissances de domaine Une représentation efficace Cependant, les paramètres d'équation et même les formes d'équation de nombreux problèmes réels sont incertains, ce qui rend difficile l'écriture d'équations de contrôle précises, ce qui limite considérablement l'application des connaissances du domaine dans l'apprentissage automatique.
SGA-PDE utilise les mathématiques symboliques pour transformer des équations et résout le problème de la représentation de toute forme d'équations aux dérivées partielles. De plus, SGA-PDE utilise un algorithme génétique conçu pour les arbres binaires et, grâce à l'optimisation itérative de la topologie et des attributs des nœuds de l'arbre, exploite automatiquement les équations de contrôle qui correspondent aux données d'observation du domaine ouvert. En optimisation, SGA-PDE ne s'appuie pas sur des informations préalables sous forme d'équations, et n'a pas non plus besoin de lui fournir un ensemble de candidats, réalisant ainsi une optimisation automatique d'équations structurelles complexes. Dans le même temps, SGA-PDE est également un algorithme sans gradient, qui évite le problème du calcul difficile du gradient entre la structure de l'équation et la valeur de la perte. Les recherches futures se concentreront sur : 1. Essayer de combiner des algorithmes d'apprentissage par renforcement ou d'optimisation combinatoire ; 2. Réduire l'espace de solution en intégrant des mécanismes physiques ; 3. Évaluer et améliorer l'applicabilité du SGA-PDE aux données clairsemées et aux données bruitées ; . Intégrer les méthodes d'intégration des connaissances aux méthodes de découverte des connaissances.
Lien papier (disponible gratuitement) :
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.023174
Code et exemple de lien de données :
https://github.com/ YuntianChen /SGA-PDE
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

