Une brève analyse de l'apprentissage automatique et des équations différentielles

Bien que l'apprentissage automatique existe depuis les années 1950, à mesure que les ordinateurs sont devenus plus puissants et que les données ont explosé, de nombreuses recherches ont été menées sur la manière dont les gens peuvent utiliser l'intelligence artificielle pour obtenir un avantage concurrentiel, améliorer leurs connaissances et augmenter leurs profits. Pour différents scénarios d'application, l'apprentissage automatique et les équations différentielles proposent un large éventail de scénarios.​

Tout le monde a déjà utilisé le machine learning, notamment le deep learning basé sur les réseaux de neurones, qui est très populaire. Avez-vous encore besoin de comprendre en profondeur les équations différentielles ? Quelle que soit la réponse, cela impliquera une comparaison entre les deux. Alors, quelle est la différence entre l’apprentissage automatique et les équations différentielles ?

Commencez par les équations différentielles du modèle amoureux

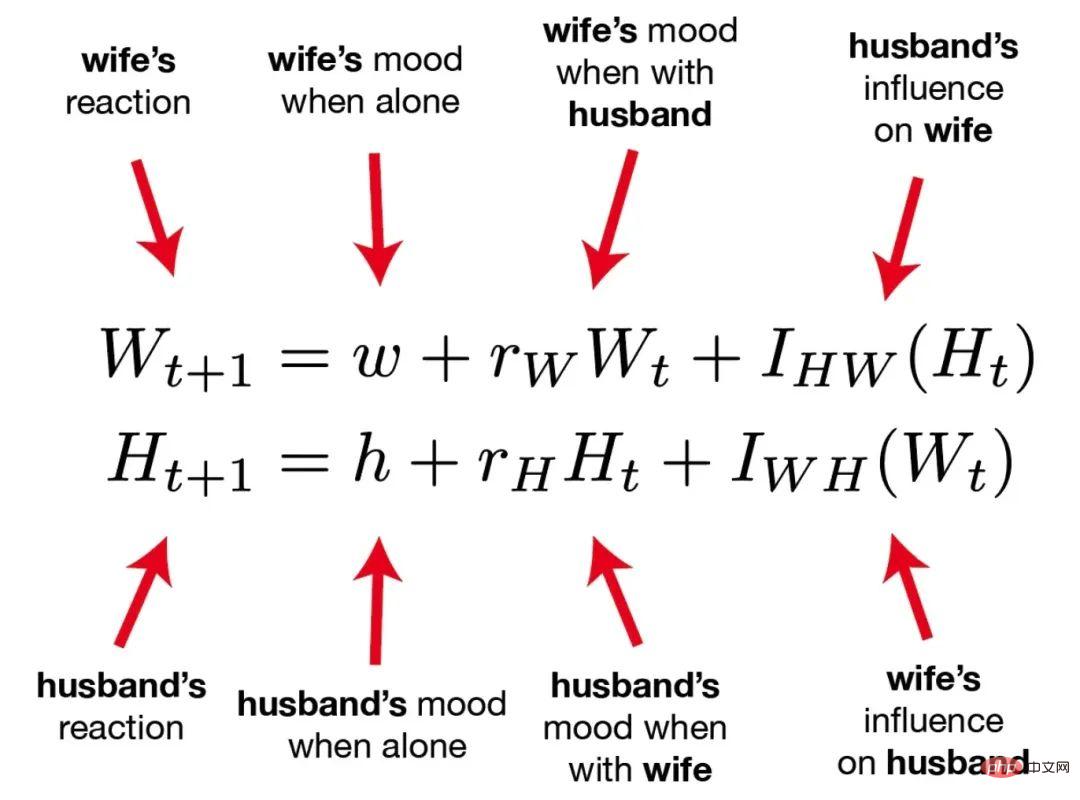
Ces deux équations prédisent la longévité de la relation amoureuse d'un couple. Basé sur les travaux pionniers du psychologue John Gottman, ce modèle prédit que les émotions positives soutenues sont la clé. au mariage. Un puissant facteur de réussite. Pour plus d'interprétation du modèle, vous pouvez vous référer au livre "Happy Marriage". L'auteur donne également 7 règles pour maintenir un mariage heureux :

1. Améliorez votre carte d'amour
2. Cultivez votre amour et vos éloges pour votre conjoint
3. Restez plus proches les uns des autres plutôt que loin
4. Laissez votre conjoint influencer votre décision
5. Commencez par la douceur et terminez par le compromis
6. Apprenez à vivre en harmonie avec les problèmes
7. Créez un sens commun

Tout le monde a vécu l'épidémie pendant trois ans, et nous savons ce qui est bon et mauvais. Alors, comment utiliser les équations différentielles pour décrire la relation entre patients et personnes contagieuses ?

Le modèle SIR suppose que le virus se propage par contact direct entre des personnes infectées et non infectées, les personnes malades se rétablissant automatiquement à un rythme fixe.

Ces équations différentielles contiennent toutes les dérivées (c'est-à-dire le taux de changement) de certaines fonctions inconnues, telles que S (t), I (t) et R (t) dans le modèle SIR, sont appelées solutions. à l'équation différentielle. Sur la base de la mécanique de ces équations, nous pouvons déduire comment le modèle est conçu, et les données seront ensuite utilisées pour vérifier nos hypothèses.

Classification des modèles mathématiques

Les modèles mathématiques comme les équations différentielles font à l'avance des hypothèses sur le mécanisme de base du système. En fait, tout le domaine de la modélisation mathématique a commencé au 17ème siècle pour démêler le mouvement planétaire. de la dynamique fondamentale qui se cache derrière. Depuis lors, les modèles mécanistiques fondés sur les mathématiques ont permis de mieux comprendre de nombreux phénomènes, depuis la biologie et l’ingénierie jusqu’à l’économie et les sciences sociales. De tels modèles de mécanismes peuvent être divisés en modèles basés sur des équations, tels que des équations différentielles, ou des modèles basés sur des agents.

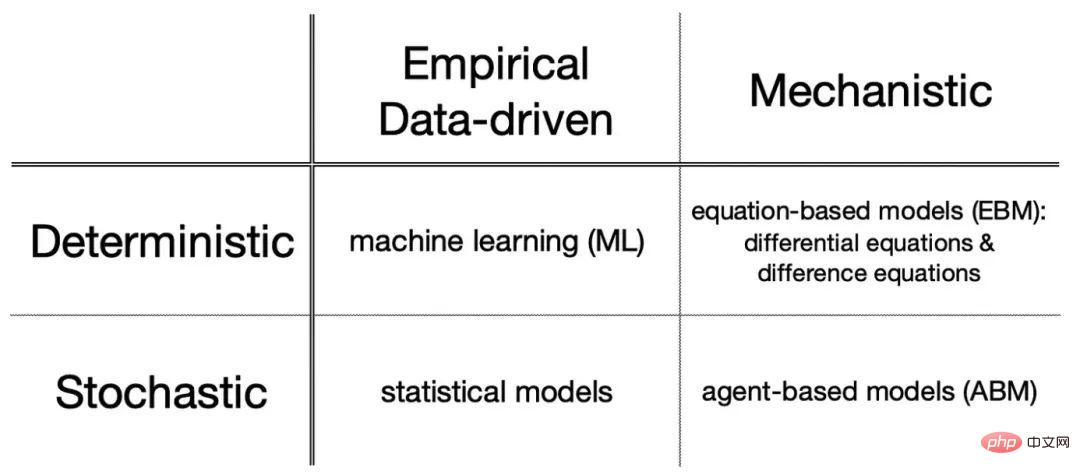
La modélisation basée sur l'expérience ou basée sur les données, comme l'apprentissage automatique, consiste à comprendre la structure d'un système grâce à des données riches. L'apprentissage automatique est particulièrement utile pour les systèmes complexes dans lesquels nous ne savons pas vraiment comment séparer le signal du bruit, et la simple formation d'un algorithme intelligent peut aider à résoudre le problème.

Les tâches d'apprentissage automatique peuvent être grossièrement divisées dans les catégories suivantes :

• apprentissage supervisé (par exemple, régression et classification) ;
• apprentissage non supervisé (par exemple, regroupement et réduction de dimensionnalité) ; Les systèmes avancés d’apprentissage automatique et d’intelligence artificielle sont désormais omniprésents dans notre vie quotidienne, depuis les assistants conversationnels intelligents basés sur des haut-parleurs (tels que Xiaodu) jusqu’à divers moteurs de recommandation, en passant par la technologie de reconnaissance faciale et même la voiture autonome de Tesla. Tout cela repose sur une modélisation mathématique et statistique intégrée sous des montagnes de code.
• De plus, ces modèles peuvent être classés comme « déterministes » (les prédictions sont fixes) ou « stochastiques » (les prédictions incluent le hasard).

Les modèles déterministes ignorent les variables aléatoires et prédisent toujours le même résultat dans les mêmes conditions de départ. En général, l’apprentissage automatique et les modèles basés sur des équations sont déterministes et le résultat est toujours prévisible. En d’autres termes, la sortie est entièrement déterminée par l’entrée.

Les modèles stochastiques prennent en compte les changements aléatoires dans la population en introduisant des probabilités dans le modèle. Une façon de capturer ces changements consiste à faire de chaque entité un agent distinct dans le modèle et à définir les comportements et mécanismes autorisés pour ces agents, qui ont certaines probabilités. Ce sont des modèles basés sur des agents.

Cependant, la possibilité de modéliser des acteurs individuels a un coût, et les modèles basés sur des agents sont plus réalistes. En raison du coût de calcul élevé et de l’interprétabilité du modèle, cela a inspiré un concept clé en modélisation mathématique : la complexité du modèle.

Complexité des modèles

Le dilemme de la complexité des modèles est une réalité à laquelle tous les modélisateurs sont confrontés. Notre objectif est de construire et d'optimiser des modèles qui ne sont ni trop simples ni trop complexes. Les modèles simples sont faciles à analyser, mais manquent souvent de pouvoir prédictif. Les modèles complexes peuvent paraître surréalistes, mais il est possible d’essayer de comprendre la vérité qui se cache derrière des problèmes complexes.

Nous devons faire un compromis entre simplicité et facilité d’analyse. Les modèles complexes d'apprentissage automatique s'efforcent d'apprendre le signal (c'est-à-dire la véritable structure du système) tout en rejetant le bruit (c'est-à-dire les interférences). Cela entraîne des performances médiocres du modèle sur les nouvelles données. En d’autres termes, les modèles d’apprentissage automatique sont moins généralisables.

L'acte délicat d'équilibrer la complexité d'un modèle est un "art", essayer de trouver un point idéal qui n'est ni trop simple ni trop complexe. Ce modèle idéal élimine le bruit, capture la dynamique sous-jacente de ce qui se passe et est raisonnablement explicable.

Il est important de noter que cela signifie qu'un bon modèle mathématique n'est pas toujours correct. Mais cela n'a pas d'importance. L'objectif est la généralisation, être capable d'expliquer à un public pourquoi le modèle fait ce qu'il fait, qu'il s'agisse d'universitaires, d'ingénieurs ou de chefs d'entreprise.

Tous les modèles sont faux, mais certains sont utiles. ——George Box, 1976 Dans l'apprentissage automatique et les statistiques, la complexité du modèle est appelée compromis biais-variance. Les modèles à biais élevé sont trop simples, ce qui entraîne un sous-ajustement, tandis que les modèles à variance élevée mémorisent le bruit au lieu du signal, ce qui entraîne un surajustement. Les data scientists s'efforcent d'atteindre cet équilibre délicat grâce à une sélection minutieuse d'algorithmes de formation et au réglage des hyperparamètres pertinents.

Équations différentielles vs apprentissage automatique

Dans la modélisation de mécanismes, nous observons et examinons attentivement un phénomène avant de faire des hypothèses sur le mécanisme sous-jacent du système, puis de valider le modèle avec des données. Nos hypothèses sont-elles correctes ? Si tel est le cas, puisqu’il s’agit d’un mécanisme trié sur le volet, il est tout à fait possible d’expliquer à n’importe qui quel modèle se comporte de cette façon. Si l’hypothèse est fausse, ce n’est pas grave, vous avez juste perdu du temps, ce n’est pas grave. La modélisation est après tout un essai et une erreur. Bricolez ces hypothèses ou même repartez de zéro. Modèles de mécanismes, généralement des équations sous forme d’équations différentielles, voire des modèles basés sur des agents.

Dans la modélisation basée sur les données, nous laissons d'abord les données commencer à fonctionner et construisons pour nous une vue panoramique du système. Tout ce que nous avons à faire est de garantir la qualité des données de cette machine et, espérons-le, de disposer de suffisamment de données. C’est l’apprentissage automatique. Si un phénomène est difficile à comprendre pour les gens ordinaires, une machine peut être réglée pour passer au crible le bruit et apprendre le signal insaisissable pour nous. Les tâches standard d'apprentissage automatique incluent la régression et la classification, qui sont évaluées à l'aide d'une gamme de métriques. Les réseaux neuronaux et l’apprentissage par renforcement sont également devenus populaires, permettant de créer des modèles et d’apprendre des signaux étonnamment complexes.

Bien que l'apprentissage automatique existe depuis les années 1950, à mesure que les ordinateurs sont devenus plus puissants et que les données ont explosé, la manière dont les gens peuvent utiliser l'intelligence artificielle pour obtenir un avantage concurrentiel, améliorer leurs connaissances et augmenter leurs profits s'est largement répandue. . Pour différents scénarios d'application, l'apprentissage automatique et les équations différentielles proposent un large éventail de scénarios.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!