Les principes et les solutions derrière les malentendus courants concernant le type Number en JavaScript

Cet article vous apporte des connaissances pertinentes sur JavaScript. Il présente principalement les connaissances pertinentes sur le type de nombre, y compris les principes derrière les malentendus courants sur le type de nombre et les solutions. Examinons-le ensemble, j'espère, utile à tout le monde.

[Recommandations associées : Tutoriel vidéo JavaScript, front-end Web]

Il n'existe qu'un seul type de valeur en JavaScript, qui est le type Number, qui est représenté en interne sous la forme d'un flottant double précision. type point, qui est le type double dans d'autres langages, il n'y a donc en fait pas de type entier en JavaScript. Les valeurs sont traitées comme des nombres à virgule flottante et la méthode de stockage est la même, conformément à la norme internationale IEEE 754. Par conséquent, 3 et 3,0 sont traités comme la même valeur en JavaScript :

3.0 === 3 // true

Pour le cas des entiers, la plage d'entiers pouvant être calculée avec précision est comprise entre −253-2^{53}−253 ~ 2532^{53}253 , Sans compter les deux points finaux, les entiers peuvent être utilisés en toute sécurité tant qu'ils se situent dans cette plage. En plus des décimales, les entiers peuvent également être représentés par des valeurs littérales octales ou hexadécimales. Le premier chiffre de la valeur littérale octale doit être zéro, suivi d'une séquence de chiffres octaux (0 ~ 7) si la valeur littérale est égale à zéro. hors plage, alors les zéros non significatifs seront ignorés et les valeurs suivantes seront analysées comme des décimales. Il convient de noter que cette représentation de l'octal en mode strict signalera une erreur. ES6 précise en outre que le préfixe 0o doit être. utilisé pour la représentation octale. Exemple :

(function(){
  console.log(0o11 === 011)
})()
// true
// 严格模式
(function(){
  'use strict';
  console.log(0o11 === 011)
})()
// Uncaught GyntaxError

Les deux premiers chiffres d'une valeur littérale hexadécimale doivent être 0x, suivis de n'importe quel chiffre hexadécimal (0 ~ 9 et A ~ F), où A ~ F peut être majuscule ou minuscule. ES6 a étendu la méthode d'écriture binaire, en utilisant le préfixe 0b (ou 0B).

Plus tôt, nous avons donné une brève introduction au type Number dans le runtime JavaScript, puis nous avons officiellement commencé à introduire ces problèmes courants, mais nous devons d'abord comprendre la méthode de stockage des données du type Number :

Méthode de stockage

.

Nombre en JavaScript Le type utilise une virgule flottante double précision, qui est le type double dans d'autres langages. Les nombres à virgule flottante double précision utilisent 8 octets, ou 64 bits, pour le stockage. selon la norme internationale IEEE 754. Procédures stockées En deux étapes,

• convertit le nombre à virgule flottante en nombre binaire correspondant et utilise la notation scientifique pour le représenter

• exprime le nombre converti en une valeur qui le représentera. être stockés dans l'ordinateur via la norme IEEE 754.

Selon la norme IEEE 754, tout nombre binaire à virgule flottante V peut être exprimé comme suit :

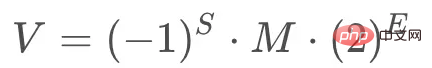
Par exemple, 5,0 en décimal s'écrit 101,0 en binaire, ce qui équivaut à 1,01*221,01 * 2^21,01* 22, où S=0, M=1,01, E=2.

IEEE 754 stipule que pour les nombres à virgule flottante de 32 bits, le bit le plus élevé est le bit de signe S, les 8 bits suivants sont l'exposant E et les 23 bits restants sont les chiffres significatifs M, comme le montre la figure ci-dessous. :

Pour 64 bits Le bit le plus élevé du nombre à virgule flottante est le bit de signe S, les 11 bits suivants sont l'exposant E et les 52 bits restants sont le chiffre significatif M, comme le montre la figure ci-dessous :

Remarque : IEEE754 Pour le chiffre significatif M et l'exposant E Il existe également des réglementations spéciales.

Comme mentionné précédemment, 1

Quant à l'indice E, la situation est plus compliquée. Tout d'abord, E est un exposant non signé, ce qui signifie que si E est de 8 bits, sa plage de valeurs est de 0 à 255, et si E est de 11 bits, sa plage de valeurs est de 0 à 2047. Mais on sait que E en notation scientifique peut avoir des valeurs négatives, donc IEEE 754 stipule que la valeur réelle de E doit être soustraite d'un nombre intermédiaire. Pour un E à 8 chiffres, ce nombre intermédiaire est 127, et pour un E à 11 chiffres. E , le nombre du milieu est 1023.

Par exemple, le E de 2102^{10}210 est 10, donc lorsqu'il est enregistré sous forme de nombre à virgule flottante de 32 bits, il doit être enregistré sous 10+127=137, soit 10001001.

Alors l'indice E peut être divisé en trois situations :

• E不全为0或不全为1：这时，浮点数就采用上面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前加上第一位的1。

• E全为0：这时，浮点数的指数E等于1 ~ 127（或1 ~ 1023），有效数字M不再加上第一位的1，而是还原成0.xxxxxxx的小数，这样做是为了表示±0，以及接近0的很小的数字。

• E全为1：这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位S）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。

示例：浮点数 9.0 如何用二进制表示？还原成十进制又是多少？

首先，浮点数 9.0 等于二进制的 1001.0，即 1.001∗231.001 *2^31.001∗23

那么，第一位的符号位 S=0，有效数字 M 等于 001 后面再加 20 个 0，凑满 23 位，指数 E 等于 3+127=130，即 10000010。

所以，写成二进制形式，应该是 S+E+M，即0 10000010 001 0000 0000 0000 0000 0000。这个 32 位的二进制数，还原成十进制，正是 1091567616。

注：虽然在 JavaScript 中无论是小数还是整数都是按照64位的浮点数形式存储，但是进行整数运算会自动转换为32位的有符号整数，例如位运算，有符号整数使用31位表示整数的数值，用第32位表示整数的符号，数值范围是−231-2^{31}−231 ~ 2312^{31}231。

二、浮点数运算的精度丢失

问题缘由

众所周知在 JavaScript 中 0.1+0.2 不等于 0.3，实际上所有浮点数值存储遵循 IEEE 754 标准的编程语言中都会存在这个问题，这是因为计算机中小数的存储先是转换成二进制进行存储的，而 0.1、0.2 转换成二进制分别为：

(0.1)10 => (00011001100110011001(1001)...)2 (0.2)10 => (00110011001100110011(0011)...)2

可以发现，0.1 和 0.2 转成二进制之后都是一个无限循环的数，前面提到尾数位只能存储最多 53 位有效数字，这时候就必须来进行四舍五入了，而这个取舍的规则就是在 IEEE 754 中定义的，0.1 最终能被存储的有效数字是

0001(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)101 + (0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)01 = 0100(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)111

最终的这个二进制数转换成十进制的就是 0.30000000000000004 ，这儿需要注意，53 位的存储位指的是能存 53 位有效数字，因此前置的 0 不算，要往后再取到  53 位有效数字为止。

因此，精度丢失的问题实际上用一句话概括就是计算机中用二进制存储小数，而大部分小数转成二进制后都是无限循环的值，因此存在取舍问题，也就是精度丢失。

解决办法

ES6 在 Number 对象上新增了一个极小常量：Number.EPSILON，值为 2.220446049250313e-16，引入这么一个常量就是为了为浮点数计算设置一个误差范围，如果这个误差小于 Number.EPSILON 我们就认为得到了准确结果。

三、大整数的运算精度丢失及溢出

问题缘由

在介绍问题的具体缘由之前我想先给大家介绍一下所谓最大安全整数范围以及最大数字绝对值的范围是如何得到的？

JavaScript 能够表示的数字的绝对值范围是 5e-324 ~ 1.7976931348623157e+308，这两个取值可以通过 Number.MIN_VALUE 和 Number.MAX_VALUE 这两个字段来表示，如果某次计算的结果得到了一个超出 JavaScript 数值范围的，那么这个数值会自动被转换为特殊的 Infinity 值，具体来说，如果这个数是负数，则会被转换成 -Infinity（负无穷），如果这个数值是正数，则会被转换成 Infinity（正无穷）。

示例：

console.log(Number.MAX_VALUE) // 1.7976931348623157e+308
console.log(Number.MIN_VALUE) // 5e-324
console.log(Number.MAX_VALUE + Number.MAX_VALUE) // Infinity

那么这个取值范围是如何得到的呢？

前面说到 JavaScript 中数值的保存采用的是双精度浮点型，遵循 IEEE 754 标准，在 ECMAScript 规范中规定指数 E 的范围在 -1074 ~ 971，双精度浮点型中有效数字 M 的存储位为52，但是有效数字 M 由于可以省略第一位1，节省一个存储位，因此有效数字M可以存储的范围为 1 ~ 2532^{53}253，因此 JavaScript 中 Number 能表示的最大数字绝对值范围是 2−10742^{-1074}2−1074 ~ 253+9712^{53+971}253+971。

注：通过 Number.isFinite()（ES6引入）和 isFinite() 方法可以判断一个数值是不是有穷的，即如果参数位于最小与最大数值之间时会返回 true。

让我们回归主题，为什么会出现大整数的运算精度丢失及溢出呢？

JavaScript 中最大安全整数的范围是 −253-2^{53}−253 ~ 2532^{53}253，不包括两个端点，即 -9007199254740991 ~ 9007199254740991，可以通过 Number.MIN_SAFE_INTEGER 和 Number.MAX_SAFE_INTEGER 字段查询，超出这个范围的整数计算都是不准确的，例如：

console.log(Number.MAX_SAFE_INTEGER) // 9007199254740991
console.log(Number.MIN_SAFE_INTEGER) // -9007199254740991
console.log(9007199254740991 + 2) // 9007199254740992

最大安全整数9007199254740991对应的二进制数如图：

53位有效数字都存储满了之后，想要表示更大的数字，就只能往指数数加一位，这时候尾数因为没有多余的存储空间，因此只能补0。

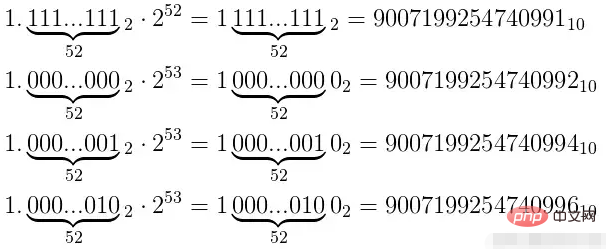
如图所示，在指数位为53的情况下，最后一位尾数位为0的数字可以被精确表示，而最后一位尾数位为1的数字都不能被精确表示。也就是可以被精确表示和不能被精确表示的比例是1:1。

同理，当指数为54的时候，只有最后两位尾数为00的可以被精确表示，也就是可以被精确表示和不能被精确表示的比例是1:3，当有效位数达到 x(x>53) 的时候，可以被精确表示和不能被精确表示的比例将是1 : 2^(x-53)^ - 1。

可以预见的是，在指数越来越高的时候，这个指数会成指数增长，因此在 Number.MAX_SAFE_INTEGER ~ Number.MAX_VALUE 之间可以被精确表示的整数可以说是凤毛麟角。

之所以会有最大安全整数这个概念，本质上还是因为数字类型在计算机中的存储结构。在尾数位不够补零之后，只要是多余的尾数为1所对应的整数都不能被精确表示。

可以发现，不管是浮点数计算的计算结果错误和大整数的计算结果错误，最终都可以归结到JS的精度只有53位（尾数只能存储53位的有效数字）。

解决办法

那么我们在日常工作中碰到这两个问题该如何解决呢？

大而全的解决方案就是使用 mathjs，看一下 mathjs 的输出：

math.config({
    number: 'BigNumber',      
    precision: 64 
});
console.log(math.format(math.eval('0.1 + 0.2'))); // '0.3'
console.log(math.format(math.eval('0.23 * 0.34 * 0.92'))); // '0.071944'
console.log(math.format(math.eval('9007199254740991 + 2'))); 
// '9.007199254740993e+15'

【相关推荐：JavaScript视频教程、web前端】

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!