En savoir plus sur l'algorithme de comparaison double dans Vue

L'algorithme

diff est la partie la plus complexe du moteur de rendu. Cet article vous présentera l'algorithme de comparaison double dans Vue. J'espère qu'il vous sera utile !

Vue et React sont tous deux des frameworks frontaux basés sur vdom. Le rendu des composants renverra vdom, et le moteur de rendu synchronisera vdom avec dom via l'API d'ajout, de suppression et de modification. (Partage vidéo d'apprentissage : Tutoriel vidéo Vuejs)

Lors du nouveau rendu, un nouveau vdom sera généré. Le moteur de rendu comparera les deux arbres vdom et mettra à jour la différence avec le dom via l'API d'ajout, de suppression et de modification.

L'algorithme qui compare deux arbres vdom et trouve les différences s'appelle l'algorithme diff.

L'algorithme de comparaison est la partie la plus complexe du moteur de rendu et constitue également une question brûlante dans les entretiens. Aujourd'hui, nous allons explorer l'algorithme diff via l'algorithme diff de Vue.

algorithme de comparaison

Nous savons que la complexité de la comparaison de deux arbres est O(n^3), car chaque nœud doit être comparé à tous les nœuds de l'autre arbre, qui est n , si un nœud modifié est trouvé, la complexité de l'exécution de l'insertion, de la suppression et de la modification est également n. Cela est vrai pour tous les nœuds, multipliés par n, donc la complexité est O(n * n * n).

Une telle complexité est inacceptable pour un framework front-end, ce qui signifie que 1000 nœuds doivent être traités 1000*1000*1000 pour un rendu, soit un total d'1 milliard de fois.

Ainsi le diff du framework front-end s'accorde sur deux principes de traitement : Comparez uniquement la même couche, et si le type change, les nœuds enfants ne seront plus comparés.

Parce que le mouvement inter-niveaux des nœuds DOM est relativement rare. Généralement, il s'agit de l'ajout, de la suppression et de la modification du DOM au même niveau.

De cette façon, vous n'avez besoin de parcourir qu'une seule fois et de comparer les types. La complexité est O(n). De plus, si le type change, les nœuds enfants ne seront plus comparés, ce qui peut économiser le parcours d'un grand nombre. de nœuds. De plus, étant donné que les nœuds dom associés sont enregistrés dans vdom, il n'est pas nécessaire de procéder à l'ajout, à la suppression et à la modification de dom, qui est O(1). La complexité globale de l'algorithme de diff est de complexité O(n).

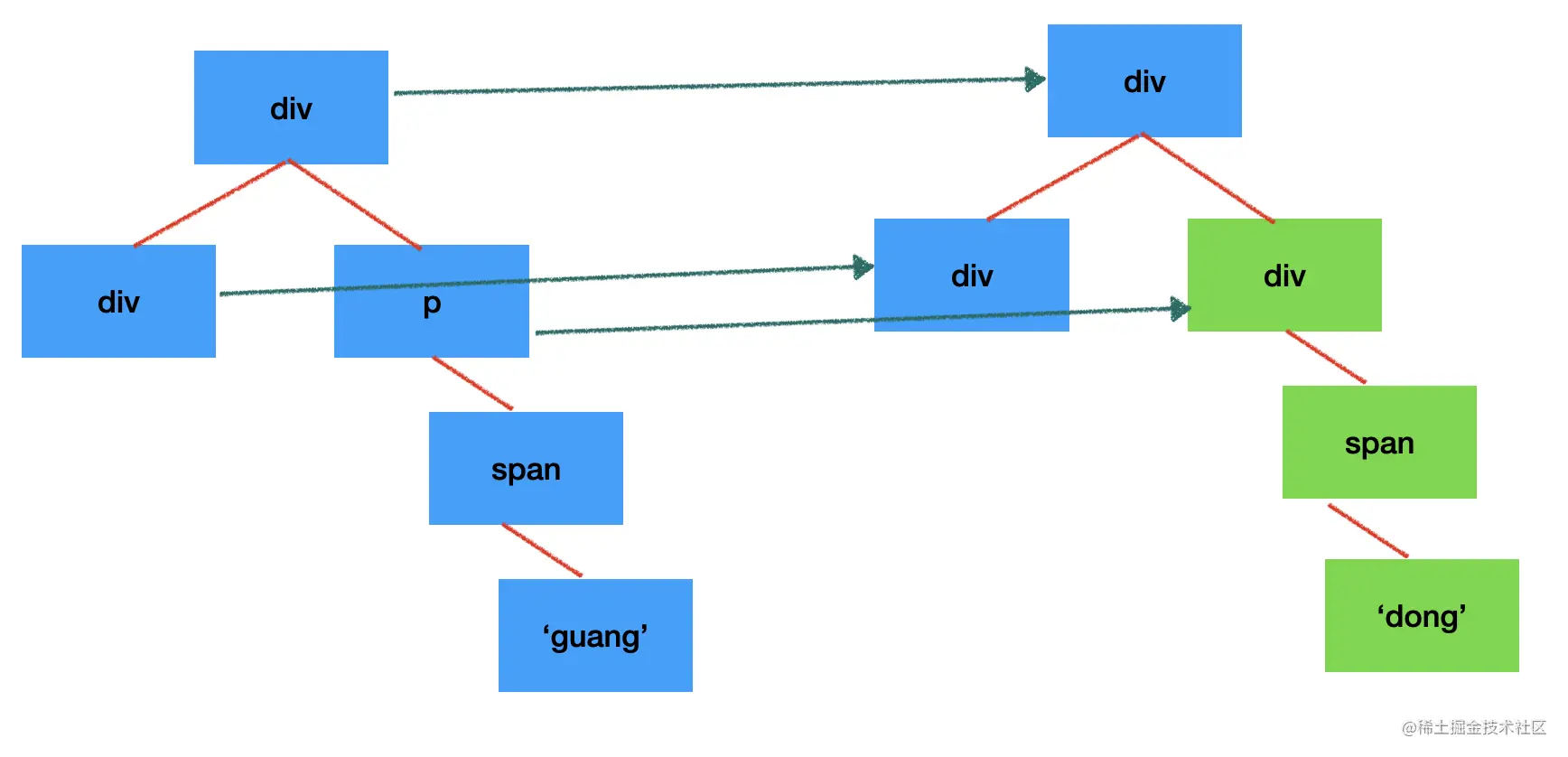
1000 nœuds sont rendus et comparés jusqu'à 1000 fois à la fois. Cette complexité se situe dans la plage acceptable.

Mais bien qu’un tel algorithme soit moins complexe, il pose encore des problèmes.

Par exemple, s'il y a 5 nœuds dans un ensemble, le type est ABCDE, et le prochain rendu sera EABCD. Si vous les comparez un par un et constatez que le type est différent, les 5 nœuds seront restitués. .

De plus, selon le principe des différents types, les nœuds enfants ne sont plus comparés. Si ces nœuds ont des nœuds enfants, ils seront également restitués.

Le fonctionnement de dom est relativement lent, donc bien que la complexité de l'algorithme de comparaison soit faible, les performances de rendu ne sont pas élevées.

Ainsi, en plus de prendre en compte sa propre complexité temporelle, l'algorithme diff doit également prendre en compte un autre facteur : le nombre d'opérations dom.

Dans l'exemple ci-dessus, ABCDE se transforme en EABCD. Évidemment, il vous suffit de déplacer E, et il n'est pas du tout nécessaire de créer un nouvel élément.

Mais comment comparer et découvrir que le même nœud a bougé ?

Déterminer le type ? Cela ne fonctionnera pas. Il peut y avoir plusieurs nœuds du même type et ils ne peuvent pas être distingués.

Il est préférable que chaque nœud ait un identifiant unique.

Ainsi, lors du rendu d'un groupe de nœuds, le framework front-end permettra au développeur de spécifier la clé et d'utiliser la clé pour déterminer si certains nœuds viennent de se déplacer, afin qu'ils puissent être réutilisés directement.

De cette façon, lorsque l'algorithme diff traite la comparaison d'un groupe de nœuds, il doit à nouveau optimiser l'algorithme en fonction de la clé.

Nous appellerons l'algorithme de comparaison de deux ensembles de nœuds basé sur la clé algorithme de comparaison multi-nœuds, qui fait partie de l'algorithme de comparaison de l'ensemble du vdom.

Ensuite, apprenons l'algorithme de comparaison multi-nœuds :

Diff simple

Supposons que vous rendiez un ensemble de nœuds ABCD, puis que vous restituiez à nouveau DCAB. Comment gérer cela ?

Le but de l'algorithme de comparaison multi-nœuds est de réutiliser les nœuds autant que possible et de remplacer la création par le déplacement des nœuds.

Donc, pour chaque nœud du nouveau tableau vnode, nous devons savoir s'il existe une clé correspondante dans l'ancien tableau vnode. Si c'est le cas, déplacez-la vers la nouvelle position. Sinon, créez-en une nouvelle.

Voici à quoi cela ressemble :

const oldChildren = n1.children
const newChildren = n2.children

let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < newChildren.length; i++) {
    const newVNode = newChildren[i]
    let j = 0
    let find = false
    // 遍历旧的 children
    for (j; j < oldChildren.length; j++) {
      const oldVNode = oldChildren[j]
      // 如果找到了具有相同 key 值的两个节点，则调用 patch 函数更新
      if (newVNode.key === oldVNode.key) {
        find = true
        patch(oldVNode, newVNode, container)
        
        处理移动...
        
        break //跳出循环，处理下一个节点
      }
   }
   // 没有找到就是新增了
   if (!find) {
      const prevVNode = newChildren[i - 1]
      let anchor = null
      if (prevVNode) {
        anchor = prevVNode.el.nextSibling
      } else {
        anchor = container.firstChild
      }
      patch(null, newVNode, container, anchor)
   }
}

La fonction du patch ici consiste à mettre à jour les propriétés du nœud et à réinitialiser l'écouteur d'événements. S'il n'y a pas d'ancien nœud correspondant, le nœud est inséré et un nœud après lui doit être transmis comme ancre d'ancrage.

Nous parcourons et traitons le nouveau vnode :

Trouvez d'abord le nœud correspondant dans l'ancien tableau de vnode. S'il est trouvé, cela signifie qu'il peut être réutilisé. Ensuite, déplacez-le.

S'il n'est pas trouvé, effectuez l'insertion et le point d'ancrage est le prochain frère du nœud précédent.

那如果找到了可复用的节点之后，那移动到哪里呢？

其实新的 vnode 数组中记录的顺序就是目标的顺序。所以把对应的节点按照新 vnode 数组的顺序来移动就好了。

const prevVNode = newChildren[i - 1]
if (prevVNode) {
    const anchor = prevVNode.el.nextSibling
    insert(newVNode.el, container, anchor)
}

要插入到 i 的位置，那就要取 i-1 位置的节点的 nextSibling 做为锚点来插入当前节点。

但是并不是所有的节点都需要移动，比如处理到第二个新的 vnode，发现它在旧的 vnode 数组中的下标为 4，说明本来就是在后面了，那就不需要移动了。反之，如果是 vnode 查找到的对应的旧的 vnode 在当前 index 之前才需要移动。

也就是这样：

let j = 0
let find = false
// 遍历旧的 children
for (j; j < oldChildren.length; j++) {
    const oldVNode = oldChildren[j]
    // 如果找到了具有相同 key 值的两个节点，则调用 patch 函数更新之
    if (newVNode.key === oldVNode.key) {
        find = true
        patch(oldVNode, newVNode, container)

        if (j < lastIndex) { // 旧的 vnode 数组的下标在上一个 index 之前，需要移动
          const prevVNode = newChildren[i - 1]
          if (prevVNode) {
            const anchor = prevVNode.el.nextSibling
            insert(newVNode.el, container, anchor)
          }
        } else {// 不需要移动
          // 更新 lastIndex
          lastIndex = j
        }
        break
    }
}

查找新的 vnode 在旧的 vnode 数组中的下标，如果找到了的话，说明对应的 dom 就是可以复用的，先 patch 一下，然后移动。

移动的话判断下下标是否在 lastIndex 之后，如果本来就在后面，那就不用移动，更新下 lastIndex 就行。

如果下标在 lastIndex 之前，说明需要移动，移动到的位置前面分析过了，就是就是新 vnode 数组 i-1 的后面。

这样，我们就完成了 dom 节点的复用和移动。

新的 vnode 数组全部处理完后，旧的 vnode 数组可能还剩下一些不再需要的，那就删除它们：

// 遍历旧的节点
for (let i = 0; i < oldChildren.length; i++) {
    const oldVNode = oldChildren[i]
    // 拿着旧 VNode 去新 children 中寻找相同的节点
    const has = newChildren.find(
      vnode => vnode.key === oldVNode.key
    )
    if (!has) {
      // 如果没有找到相同的节点，则移除
      unmount(oldVNode)
    }
}

这样，我们就完成了两组 vnode 的 diff 和对应 dom 的增删改。

小结一下：

diff 算法的目的是根据 key 复用 dom 节点，通过移动节点而不是创建新节点来减少 dom 操作。

对于每个新的 vnode，在旧的 vnode 中根据 key 查找一下，如果没查找到，那就新增 dom 节点，如果查找到了，那就可以复用。

复用的话要不要移动要判断下下标，如果下标在 lastIndex 之后，就不需要移动，因为本来就在后面，反之就需要移动。

最后，把旧的 vnode 中在新 vnode 中没有的节点从 dom 树中删除。

这就是一个完整的 diff 算法的实现。

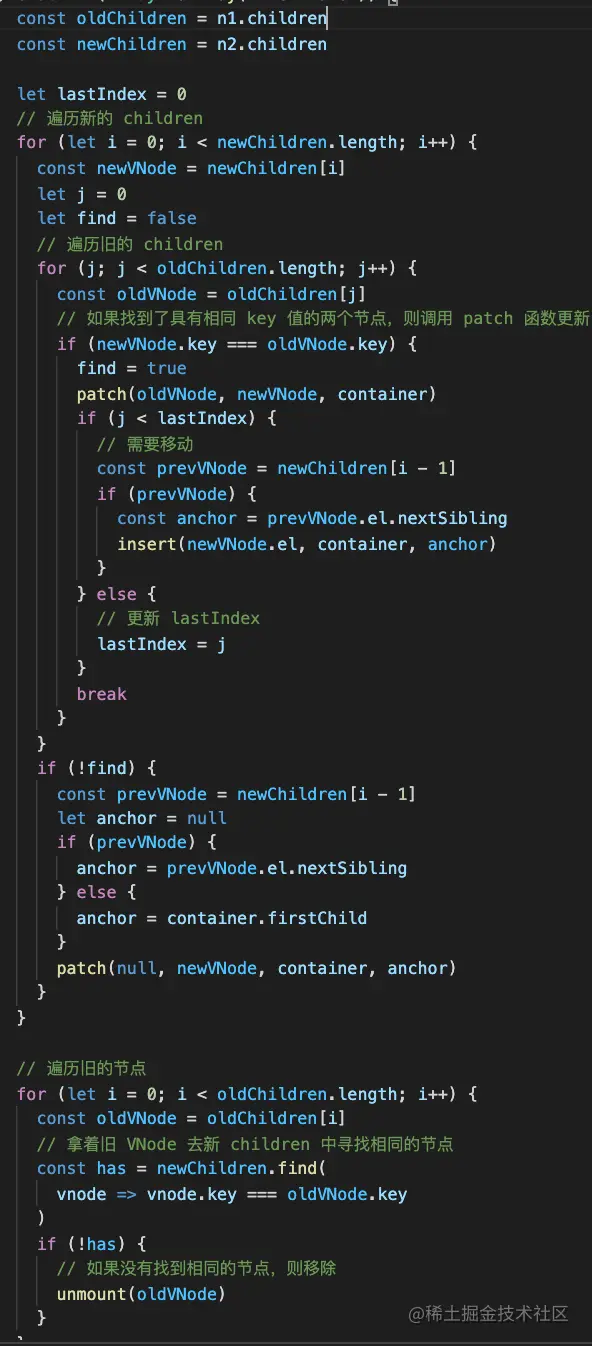
这个 diff 算法我们是从一端逐个处理的，叫做简单 diff 算法。

简单 diff 算法其实性能不是最好的，比如旧的 vnode 数组是 ABCD，新的 vnode 数组是 DABC，按照简单 diff 算法，A、B、C 都需要移动。

那怎么优化这个算法呢？

从一个方向顺序处理会有这个问题，那从两个方向同时对比呢？

这就是双端 diff 算法：

双端 diff

简单 diff 算法能够实现 dom 节点的复用，但有的时候会做一些没必要的移动。双端 diff 算法解决了这个问题，它是从两端进行对比。

我们需要 4 个指针，分别指向新旧两个 vnode 数组的头尾：

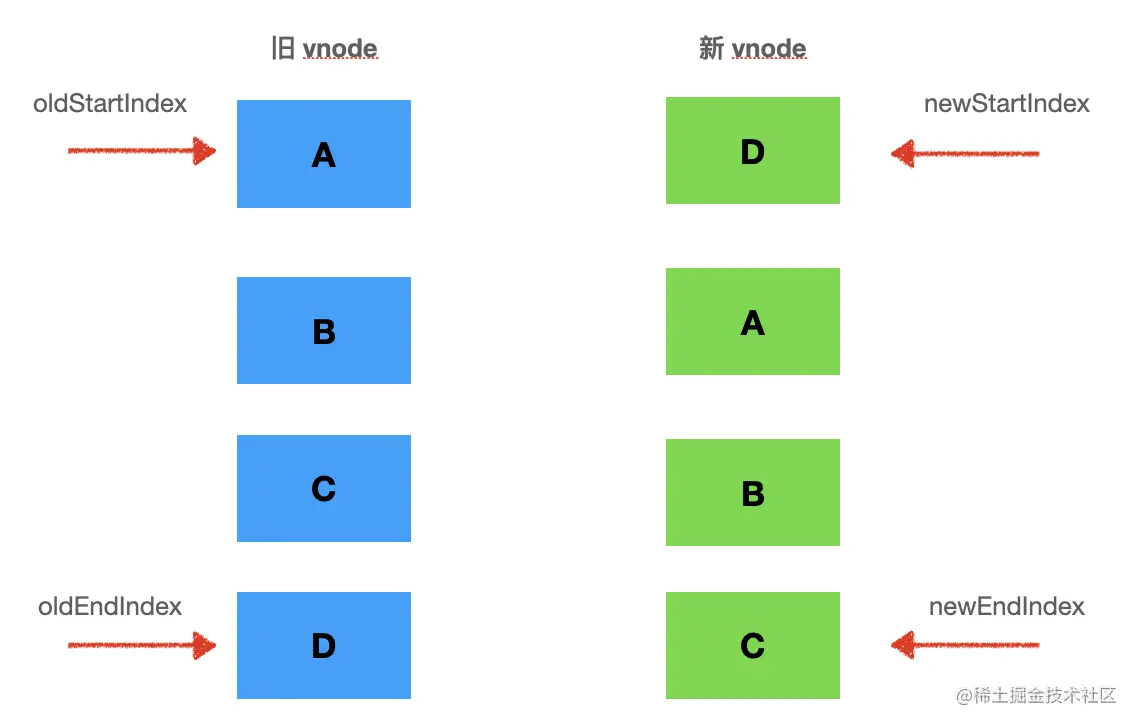
头和尾的指针向中间移动，直到 oldStartIdx

每次对比下两个头指针指向的节点、两个尾指针指向的节点，头和尾指向的节点，是不是 key是一样的，也就是可复用的。

如果是可复用的话就直接用，调用 patch 更新一下，如果是头尾这种，还要移动下位置。

也就是这样的：

while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) { // 头头
    patch(oldStartVNode, newStartVNode, container)
    oldStartVNode = oldChildren[++oldStartIdx]
    newStartVNode = newChildren[++newStartIdx]
  } else if (oldEndVNode.key === newEndVNode.key) {//尾尾
    patch(oldEndVNode, newEndVNode, container)
    oldEndVNode = oldChildren[--oldEndIdx]
    newEndVNode = newChildren[--newEndIdx]
  } else if (oldStartVNode.key === newEndVNode.key) {//头尾，需要移动
    patch(oldStartVNode, newEndVNode, container)
    insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)

    oldStartVNode = oldChildren[++oldStartIdx]
    newEndVNode = newChildren[--newEndIdx]
  } else if (oldEndVNode.key === newStartVNode.key) {//尾头，需要移动
    patch(oldEndVNode, newStartVNode, container)
    insert(oldEndVNode.el, container, oldStartVNode.el)

    oldEndVNode = oldChildren[--oldEndIdx]
    newStartVNode = newChildren[++newStartIdx]
  } else {
    
    // 头尾没有找到可复用的节点
  }
}

头头和尾尾的对比比较简单，头尾和尾头的对比还要移动下节点。

比如旧 vnode 的头节点是新的 vnode 的尾节点，那就要把它移动到旧的 vnode 的尾节点的位置。

也就是：

insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)

插入节点的锚点节点是 oldEndVNode 对应的 dom 节点的 nextSibling。

如果旧 vnode 的尾节点是新 vnode 的头结点，那就要把它移动到旧 vnode 的头结点的位置。

也就是：

insert(oldEndVNode.el, container, oldStartVNode.el)

插入节点的锚点节点是 oldStartVNode 对应的 dom 节点（因为要插在它之前）。

从双端进行对比，能尽可能的减少节点移动的次数。

当然，还要处理下如果双端都没有可复用节点的情况：

如果双端都没有可复用节点，那就在旧节点数组中找，找到了就把它移动过来，并且原位置置为 undefined。没找到的话就插入一个新的节点。

也就是这样：

const idxInOld = oldChildren.findIndex(
  node => node.key === newStartVNode.key
)
if (idxInOld > 0) {
  const vnodeToMove = oldChildren[idxInOld]
  patch(vnodeToMove, newStartVNode, container)
  insert(vnodeToMove.el, container, oldStartVNode.el)
  oldChildren[idxInOld] = undefined
} else {
  patch(null, newStartVNode, container, oldStartVNode.el)
}

因为有了一些 undefined 的节点，所以要加上空节点的处理逻辑：

if (!oldStartVNode) {
    oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
    oldEndVNode = newChildren[--oldEndIdx]
}

这样就完成了节点的复用和移动的逻辑。

那确实没有可复用的节点的那些节点呢？

经过前面的移动之后，剩下的节点都被移动到了中间，如果新 vnode 有剩余，那就批量的新增，如果旧 vnode 有剩余那就批量的删除。

因为前面一个循环的判断条件是 oldStartIdx

所以判断条件是这样的：

if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
  // 添加新节点
  for (let i = newStartIdx; i <= newEndIdx; i++) {
    patch(null, newChildren[i], container, oldStartVNode.el)
  }
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
  // 移除操作
  for (let i = oldStartIdx; i <= oldEndIdx; i++) {
    unmount(oldChildren[i])
  }
}

这样就是一个完整的 diff 算法了，包括查找可复用节点和移动节点、新增和删除节点。

而且因为从两侧查找节点，会比简单 diff 算法性能更好一些。

比如 ABCD 到 DABC，简单 diff 算法需要移动 ABC 三个节点，而双端 diff 算法只需要移动 D 一个节点。

小结一下：

双端 diff 是头尾指针向中间移动的同时，对比头头、尾尾、头尾、尾头是否可以复用，如果可以的话就移动对应的 dom 节点。

如果头尾没找到可复用节点就遍历 vnode 数组来查找，然后移动对应下标的节点到头部。

最后还剩下旧的 vnode 就批量删除，剩下新的 vnode 就批量新增。

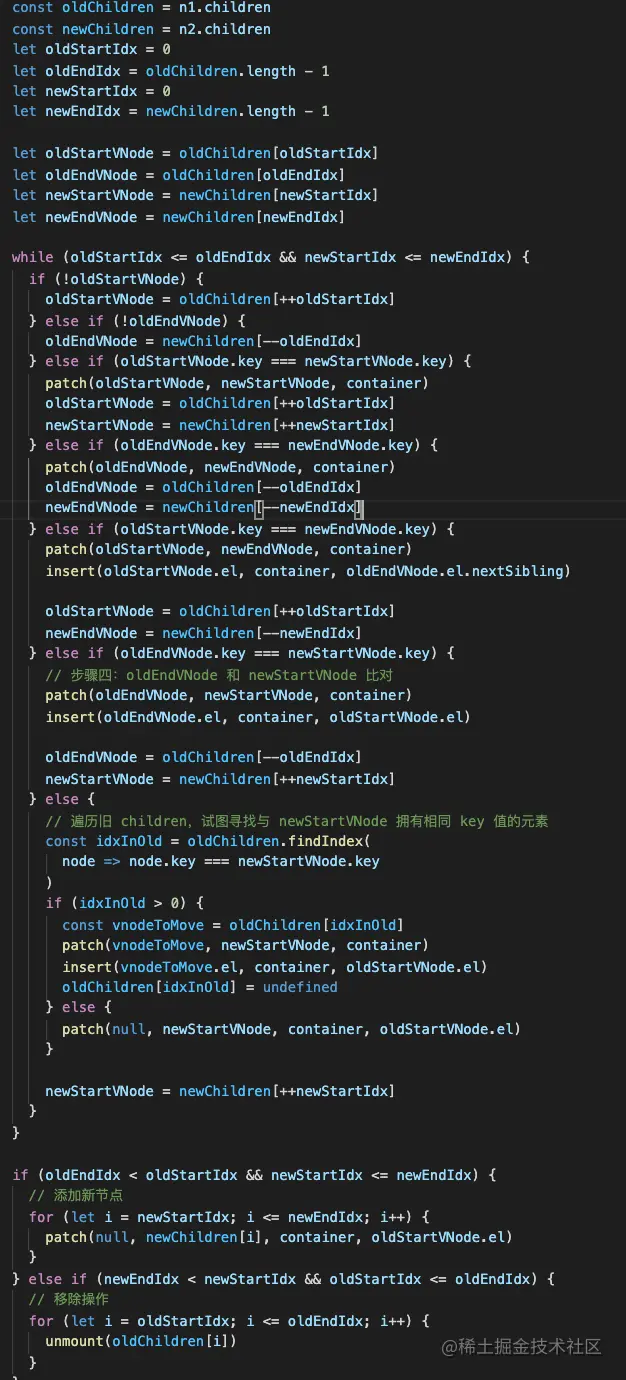
双端 diff 算法是 Vue2 采用的 diff 算法，性能还不错。

后来，Vue3 又对 diff 算法进行了一次升级，叫做快速 diff 算法。这个后面再讲。

总结

React 和 Vue 都是基于 vdom 的前端框架，组件产生 vdom，渲染器再把 vdom 通过增删改的 dom api 更新到 dom。

当再次渲染出 vdom 时，就要新旧两棵 vdom 树做 diff，只更新变化的 dom 节点。

两棵树的 diff 是 O(n^3) 的，时间复杂度太高，因此前端框架规定了只做同层 diff，还有 type 不一样就认为节点不一样，不再对比子节点。这样时间复杂度一下子就降到了 O(n)。

但是对于多个子字节点的 diff 不能粗暴的删除和新增，要尽量复用已有的节点，也就是通过移动代替新增。

所以多节点的时候，要指定 key，然后 diff 算法根据 key 来查找和复用节点。

简单 diff 算法是依次根据 key 查找旧节点的，移动的话通过 lastIndex 判断，大于它就不用动，小于它才需要移动。剩下的节点再批量删除和新增。

但是简单 diff 算法局限性还是比较大的，有些情况下性能并不好，所以 vue2 用的是双端 diff 算法。

双端 diff 算法是头尾指针向中间移动，分别判断头尾节点是否可以复用，如果没有找到可复用的节点再去遍历查找对应节点的下标，然后移动。全部处理完之后也要对剩下的节点进行批量的新增和删除。

其实 diff 算法最重要的就是找到可复用的节点，然后移动到正确的位置。只不过不同的算法查找顺序不一样。

vue2 是用的双端 diff 的算法，而 vue3 则通过最长递增子序列的算法做了进一步的优化，关于优化后的 diff 算法，我们之后再聊。

【相关视频教程推荐：web前端】

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!