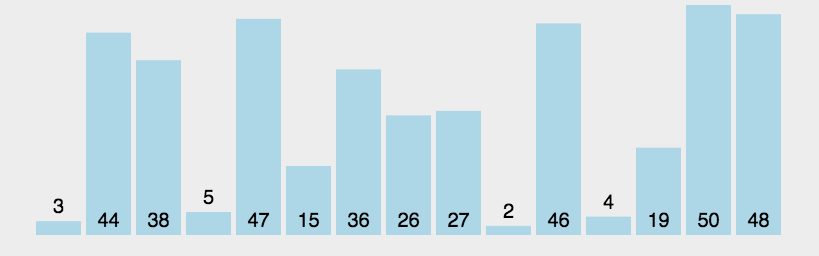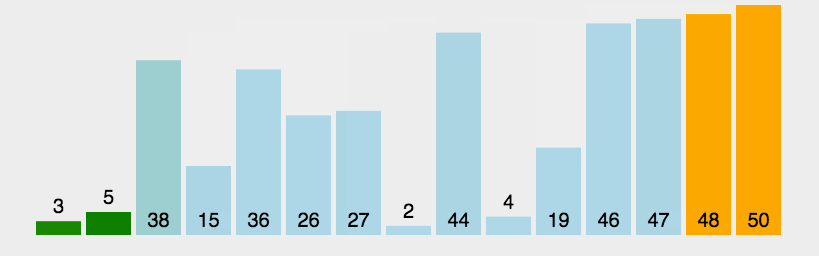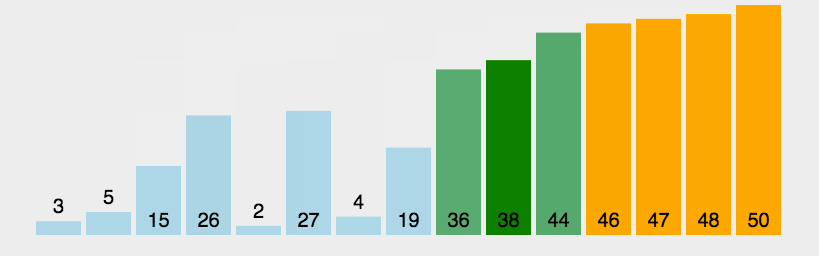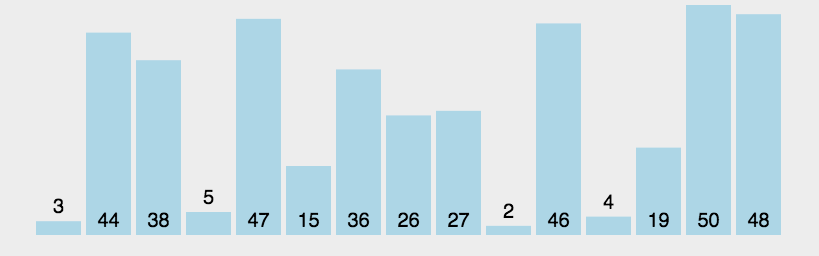Maison >développement back-end >Tutoriel Python >Explication graphique détaillée de l'algorithme de tri à bulles Python
Explication graphique détaillée de l'algorithme de tri à bulles Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2022-06-06 19:21:083596parcourir
Cet article vous apporte des connaissances pertinentes sur python. Il présente principalement des problèmes liés au tri des bulles, y compris la description des algorithmes, l'analyse, l'implémentation du code, etc. est utile.

Apprentissage recommandé : Tutoriel vidéo Python
1 Description de l'algorithme
Bubble Sort (Bubble Sort) est un algorithme de tri simple. Il parcourt à plusieurs reprises le tableau à trier, en comparant deux éléments à la fois et en les échangeant s'ils sont dans le mauvais ordre. Le travail de parcours du tableau est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, ce qui signifie que le tableau a été trié. Le nom de cet algorithme vient du fait que les éléments plus petits « flotteront » lentement vers le haut du tableau grâce à l’échange.
2. Analyse d'algorithme
1. Si le premier est supérieur au second (par ordre croissant), échangez-les tous les deux.
2. Faites la même chose pour chaque paire d'éléments adjacents, de la première paire au début à la dernière paire à la fin. Une fois cette étape terminée, l’élément final sera le plus grand nombre.
3. Répétez les étapes ci-dessus pour tous les éléments sauf le dernier.
4. Continuez à répéter les étapes ci-dessus pour de moins en moins d'éléments à chaque fois jusqu'à ce qu'il n'y ait plus de paires de nombres à comparer.
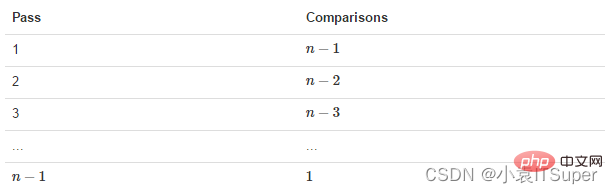
Ensuite, nous devons effectuer n-1 processus de bouillonnement, et le nombre de comparaisons correspondant pour chaque fois est comme indiqué dans la figure ci-dessous :
3. le processus en cours. Jetons un coup d'œil à l'implémentation de l'animation
:Nous trions la liste non ordonnée suivante
4. Implémentation du code
5 . Mise à niveau de l'algorithme
Code d'implémentation :import timepop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为:", pop_list)# 记录开始时间start = time.time()# 外层循环控制轮数for i in range(len(pop_list) - 1): # 内层循环控制比较次数 for j in range(len(pop_list) - i - 1): # 如果前一个数字比后一个数字大,就交换位置 if pop_list[j] > pop_list[j + 1]: # python特有交换位置方式 pop_list[j], pop_list[j + 1] = pop_list[j + 1], pop_list[j]print("排序好的列表为:", pop_list)# 记录结束时间end = time.time()print("算法总耗时:", end - start)Résultats en cours d'exécution :
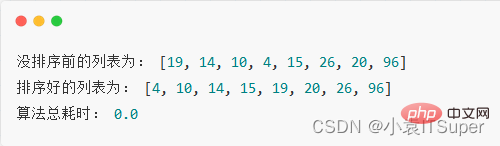
Code d'implémentation :
O(n)import timedef bubble_sort(pop_list): for j in range(len(pop_list) - 1, 0, -1): count = 0 for i in range(0, j): if pop_list[i] > pop_list[i + 1]: pop_list[i], pop_list[i + 1] = pop_list[i + 1], pop_list[i] count += 1 if count == 0: returnpop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为:", pop_list)# 记录开始时间start = time.time()bubble_sort(pop_list)print("排序好的列表为:", pop_list)# 记录结束时间end = time.time()print("算法总耗时:", end - start)Résultat de l'exécution :
6. Analyse de la complexité temporelle
🎜🎜🎜Analyse de tri : Il existe un total de 8 nombres dans le tableau à trier, 7 comparaisons ont été effectuées au premier tour de tri, 6 comparaisons ont été effectuées au deuxième tour de tri, et ainsi de suite, et 1 comparaison a été effectuée au dernier tour.La plus mauvaise complexité temporelle :
- Complexité temporelle optimale :
O(n)(Indique qu'après une traversée une fois, il s'avère qu'aucun élément ne peut être échangé et le tri se termine .)O(n)(表示遍历一次发现没有任何可以交换的元素,排序结束。)- 最坏时间复杂度:
O(n^2)- 稳定性:稳定
- 排序分析:待排数组中一共有8个数,第一轮排序时进行了7次比较,第二轮排序时进行了6比较,依次类推,最后一轮进行了1次比较。
- 数组元素总数为N时,则一共需要的比较次数为:
(N-1)+ (N-2)+ (N-3)+ ...1=N*(N-1)/2- 算法约做了
N^2/2次比较。因为只有在前面的元素比后面的元素大时才交换数据,所以交换的次数少于比较的次数。如果数据是随机的,大概有一半数据需要交换,则交换的次数为N^2/4(不过在最坏情况下,即初始数据逆序时,每次比较都需要交换)。- 交换和比较的操作次数都与 N^2 成正比,由于在大O表示法中,常数忽略不计,冒泡排序的时间复杂度为
O(N^2)O(n^2)
🎜🎜🎜🎜Lorsque le nombre total d'éléments du tableau est N, le nombre total de comparaisons requises est :
(N-1)+ (N-2)+ (N-3) + .. .1=N*(N-1)/2L'algorithme 🎜🎜🎜🎜 effectue approximativement des comparaisons
N^2/2. Étant donné que les données sont échangées uniquement lorsque l'élément précédent est supérieur à l'élément suivant, le nombre d'échanges est inférieur au nombre de comparaisons. Si les données sont aléatoires et qu'environ la moitié des données doivent être échangées, le nombre d'échanges est N^2/4 (mais dans le pire des cas, lorsque les données initiales sont dans l'ordre inverse, chaque la comparaison doit être échangée). 🎜🎜🎜🎜Le nombre d'opérations d'échange et de comparaison est proportionnel à N^2 Puisque dans la notation grand O, les constantes sont ignorées, la complexité temporelle du tri à bulles est
O (N. ^2). 🎜🎜🎜🎜🎜Apprentissage recommandé : 🎜Tutoriel vidéo Python🎜🎜Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Résumé des points de connaissances multi-processus Python
- Introduction détaillée au module numpy de python
- Explication graphique détaillée de la façon d'utiliser Python pour dessiner des graphiques de visualisation dynamique
- Exemples détaillés des quatre principales caractéristiques de Python orienté objet
- Fonctions de concaténation et de fusion d'analyse de données Python (exemples détaillés)