Maison >développement back-end >Tutoriel Python >Analysons ensemble les applications et les exercices liés aux files d'attente Python
Analysons ensemble les applications et les exercices liés aux files d'attente Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2022-03-30 18:35:142814parcourir
Cet article vous apporte des connaissances pertinentes sur python, qui présente principalement des exercices d'application liés aux files d'attente, notamment comment utiliser deux piles pour implémenter une file d'attente, comment utiliser deux files d'attente pour implémenter une pile et juger de la continuité des éléments de la pile, etc. J'espère que cela sera utile à tout le monde.

Apprentissage recommandé : Tutoriel Python
0. Objectifs d'apprentissage
Nous avons appris les concepts associés aux files d'attente et à leur mise en œuvre, et avons également compris la large application des files d'attente dans des problèmes pratiques. L'objectif principal de cette section. Il s'agit d'approfondir davantage la compréhension des files d'attente grâce à des exercices liés aux files d'attente, et en même temps, les files d'attente peuvent être utilisées pour réduire la complexité temporelle de la résolution de certains problèmes complexes.
1. Utilisez deux piles pour implémenter une file d'attente
[Question] Étant donné deux piles, implémentez une file d'attente en utilisant uniquement les opérations de base de la pile.
[Idée] La clé pour résoudre ce problème réside dans la fonction d'inversion de la pile. Une série d'éléments poussés sur la pile sera renvoyée dans l'ordre inverse lorsqu'elle sera retirée de la pile. Par conséquent, l'utilisation de deux piles peut obtenir le retour des éléments dans le même ordre (la séquence inversée des éléments sera à nouveau inversée pour obtenir l'ordre d'origine). L'opération spécifique est illustrée dans la figure ci-dessous :
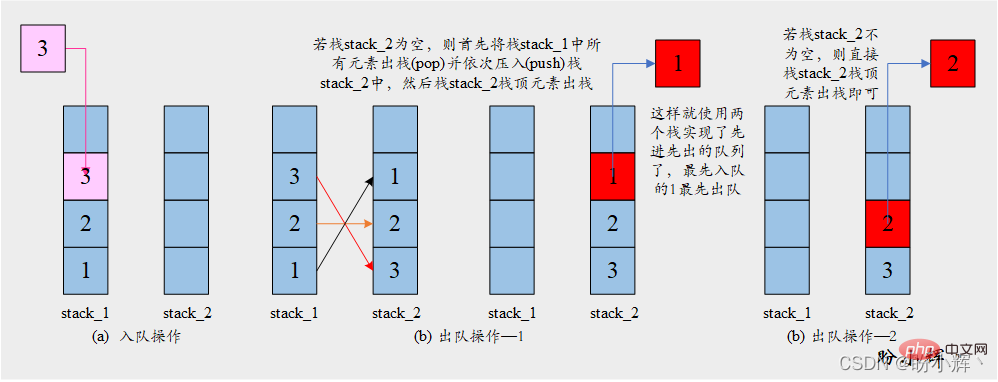
[Algorithme]
Mettre en file d'attente
mettre en file d'attente:
Pousser les éléments sur la pilestack_1
Retirerdequeue:
Si la pilestack_2n'est pas vide :
Retirerstack_2de la file d'attente : pop l'élément supérieur de la pile
Sinon :
Supprimez tous les éléments destack_1et poussez-les dansstack_2
stack_2Pop l'élément supérieur de la pileenqueue:
将元素推入栈stack_1
出队dequeue:
如果栈stack_2不为空:
stack_2栈顶元素出栈
否则:
将所有元素依次从stack_1弹出并压入stack_2
stack_2栈顶元素出栈
[代码]
class Queue: def __init__(self): self.stack_1 = Stack() self.stack_2 = Stack() def enqueue(self, data): self.stack_1.push(data) def dequeue(self): if self.stack_2.isempty(): while not self.stack_1.isempty(): self.stack_2.push(self.stack_1.pop()) return self.stack_2.pop()
[时空复杂度] 入队时间复杂度为 O(1),如果栈 stack_2 不为空,那么出队的时间复杂度为 O(1),如果栈 stack_2 为空,则需要将元素从 stack_1 转移到 stack_2,但由于 stack_2 中转移的元素数量和出队的元素数量是相等的,因此出队的摊销时间复杂度为 O(1)。
2. Analysons ensemble les applications et les exercices liés aux files dattente Python
[问题] 给定两个队列,仅使用队列的基本操作实现一个栈。
[思路] 由于队列并不具备反转顺序的特性,入队顺序即为元素的出队顺序。因此想要获取最后一个入队的元素,需要首先将之前所有元素出队。因此为了使用两个队列实现栈,我们需要将其中一个队列 store_queue 用于存储元素,另一个队列 temp_queue 则用来保存为了获取最后一个元素而保存临时出队的元素。push 操作将给定元素入队到存储队列 store_queue 中;pop 操作首先把存储队列 store_queue 中除最后一个元素外的所有元素都转移到临时队列 temp_queue 中,然后存储队列 store_queue
[Code]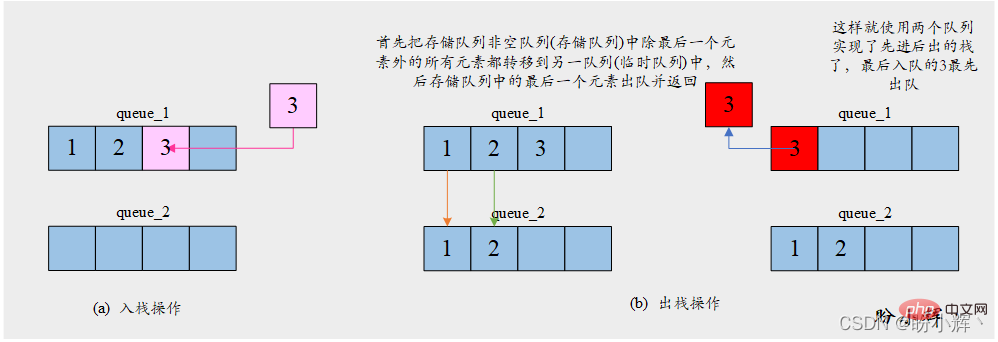
class Stack:
def __init__(self):
self.queue_1 = Queue()
self.queue_2 = Queue()
def isempty(self):
return self.queue_1.isempty() and self.queue_2.isempty()
def push(self, data):
if self.queue_2.isempty():
self.queue_1.enqueue(data)
else:
self.queue_2.enqueue(data)
def pop(self):
if self.isempty():
raise IndexError("Stack is empty")
elif self.queue_2.isempty():
while not self.queue_1.isempty():
p = self.queue_1.dequeue()
if self.queue_1.isempty():
return p
self.queue_2.enqueue(p)
else:
while not self.queue_2.isempty():
p = self.queue_2.dequeue()
if self.queue_2.isempty():
return p
self.queue_1.enqueue(p)
[Complexité temporelle et spatiale] La complexité temporelle de la mise en file d'attente est O(1) , si la pile stack_2 n'est pas vide, alors la complexité temporelle du retrait de la file d'attente est O(1) span> si la pile stack_2 est vide, les éléments doivent donc être transférés de stack_1 à stack_2, mais en raison du éléments transférés dans stack_2 Le nombre et le nombre d'éléments retirés de la file d'attente sont égaux, donc la complexité temporelle amortie de la sortie de la file d'attente est O (1).
store_queue pour stocker les éléments, et l'autre file d'attente temp_queue pour enregistrer les éléments dans récupère le dernier élément temporairement retiré de la file d'attente. L'opération push met l'élément donné en file d'attente dans la file d'attente de stockage store_queue ; l'opération pop met d'abord l'élément donné en file d'attente dans la file d'attente de stockage store_queue. Tous les éléments sauf le dernier élément sont transférés vers la file d'attente temporaire temp_queue, puis le dernier élément de la file d'attente de stockage store_queue est retiré de la file d'attente et renvoyé. L'opération spécifique est illustrée dans la figure ci-dessous : 🎜🎜🎜🎜🎜🎜[Algorithme]🎜🎜算法运行过程需要始终保持其中一个队列为空,用作临时队列
入栈push:在非空队列中插入元素data。
若队列queue_1为空:
将data插入 队列queue_2中
否则:
将data插入 队列queue_1中
出栈pop:将队列中的前n−1 个元素插入另一队列,删除并返回最后一个元素
若队列queue_1不为空:
将队列queue_1的前n−1 个元素插入queue_2,然后queue_1的最后一个元素出队并返回
若队列queue_2不为空:
将队列queue_2的前 n−1 个元素插入queue_1,然后queue_2的最后一个元素出队并返回
[代码]
class Stack:
def __init__(self):
self.queue_1 = Queue()
self.queue_2 = Queue()
def isempty(self):
return self.queue_1.isempty() and self.queue_2.isempty()
def push(self, data):
if self.queue_2.isempty():
self.queue_1.enqueue(data)
else:
self.queue_2.enqueue(data)
def pop(self):
if self.isempty():
raise IndexError("Stack is empty")
elif self.queue_2.isempty():
while not self.queue_1.isempty():
p = self.queue_1.dequeue()
if self.queue_1.isempty():
return p
self.queue_2.enqueue(p)
else:
while not self.queue_2.isempty():
p = self.queue_2.dequeue()
if self.queue_2.isempty():
return p
self.queue_1.enqueue(p)
[时空复杂度] push 操作的时间复杂度为O(1),由于 pop 操作时,都需要将所有元素从一个队列转移到另一队列,因此时间复杂度O(n)。
3. 栈中元素连续性判断
[问题] 给定一栈 stack1,栈中元素均为整数,判断栈中每对连续的数字是否为连续整数(如果栈有奇数个元素,则排除栈顶元素)。例如,输入栈 [1, 2, 5, 6, -5, -4, 11, 10, 55],输入为 True,因为排除栈顶元素 55 后,(1, 2)、(5, 6)、(-5, -4)、(11, 10) 均为连续整数。
[思路] 由于栈中可能存在奇数个元素,因此为了正确判断,首次需要将栈中元素反转,栈顶元素变为栈底,然后依次出栈,进行判断。
[算法]
栈
stack中所有元素依次出栈,并插入队列queue中
队列queue中所有元素出队,并入栈stack
while 栈stack不为空:
栈顶元素e1出栈,并插入队列queue中
如果栈stack不为空:
栈顶元素e2出栈,并插入队列queue中
如果|e1-e2|!=1:
返回False,跳出循环
队列queue中所有元素出队,并入栈stack
[代码]
def check_stack_pair(stack): queue = Queue() flag = True # 反转栈中元素 while not stack.isempty(): queue.enqueue(stack.pop()) while not queue.isempty(): stack.push(queue.dequeue()) while not stack.isempty(): e1 = stack.pop() queue.enqueue(e1) if not stack.isempty(): e2 = stack.pop() queue.enqueue(e2) if abs(e1-e2) != 1: flag = False break while not queue.isempty(): stack.push(queue.dequeue()) return flag
[时空复杂度] 时间复杂度为 O(n),空间复杂度为 O(n)。
4. Analysons ensemble les applications et les exercices liés aux files dattente Python
[问题] 给定一个整数队列 queue,将队列的前半部分与队列的后半部分交错来重新排列元素。例如输入队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9],则输出应为 [1, 6, 2, 7, 3, 8, 4, 9, 5]。
[思路] 通过获取队列的前半部分,然后利用栈的反转特性,可以实现重排操作,如下图所示:
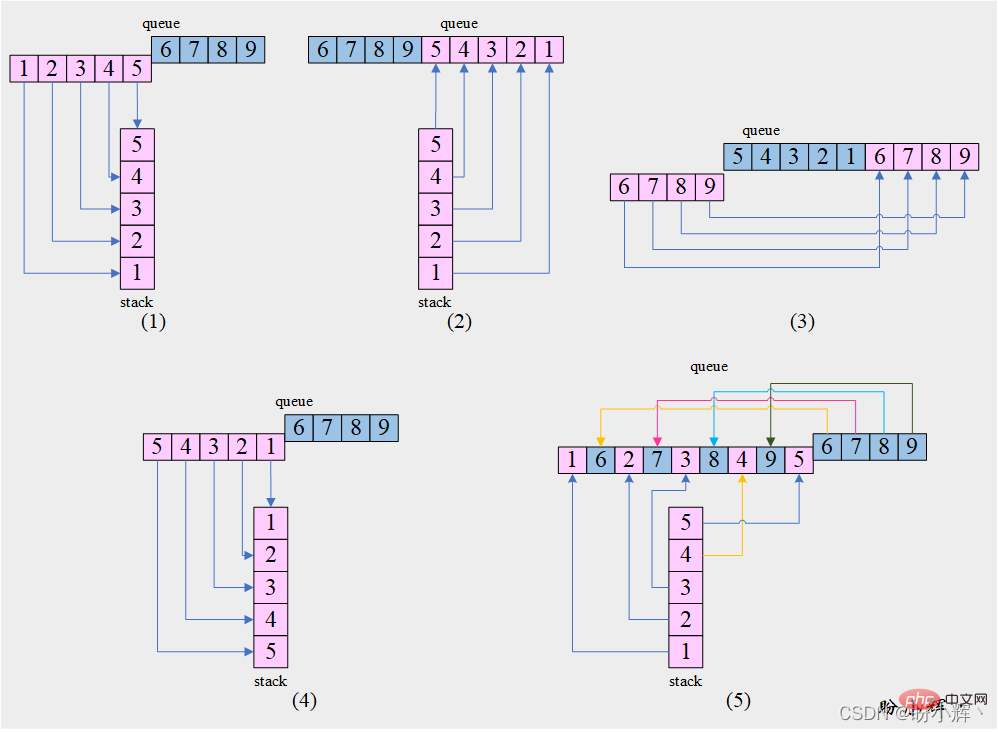
[算法]
如果队列
queue中的元素数为偶数:
half=queue.size//2
否则:
half=queue.size//2+1
1. 将队列queue的前半部分元素依次出队并入栈stack
2. 栈stack中元素出栈并入队queue
3. 将队列queue中在步骤 1中未出队的另一部分元素依次出队并插入队尾
4. 将队列queue的前半部分元素依次出队并入栈stack
5. 将栈stack和队列queue中的元素交替弹出并入队
6. 如果栈stack非空:
栈stack中元素出栈并入队
[代码]
def queue_order(queue): stack = Stack() size = queue.size if size % 2 == 0: half = queue.size//2 else: half = queue.size//2 + 1 res = queue.size - half for i in range(half): stack.push(queue.dequeue()) while not stack.isempty(): queue.enqueue(stack.pop()) for i in range(res): queue.enqueue(queue.dequeue()) for i in range(half): stack.push(queue.dequeue()) for i in range(res): queue.enqueue(stack.pop()) queue.enqueue(queue.dequeue()) if not stack.isempty(): queue.enqueue(stack.pop())
[时空复杂度] 时间复杂度为O(n),空间复杂度为 O(n)。
5. 反转队列中前 m 个元素的顺序
[问题] 给定一个整数 m 和一个整数队列 queue,反转队列中前 k 个元素的顺序,而其他元素保持不变。如 m=5,队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9],算法输出为 [5, 4, 3, 2, 1, 6, 7, 8, 9]。
[思路] 结合 [问题4] 我们可以发现,此题就是 [问题4] 的前 3 步,如下图所示:
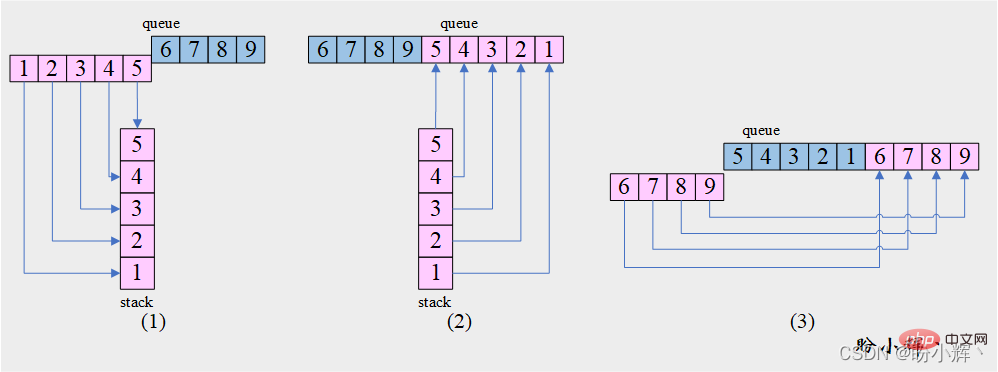
[算法]
1. 将队列
queue的前m个元素依次出队并入栈stack
2. 栈stack中元素出栈并入队queue
3. 将队列queue中在步骤 1中未出队的另一部分元素依次出队并插入队尾
[代码]
def reverse_m_element(queue, m): stack = Stack() size = queue.size if queue.isempty() or m>size: return for i in range(m): stack.push(queue.dequeue()) while not stack.isempty(): queue.enqueue(stack.pop()) for i in range(size-m): queue.enqueue(queue.dequeue())
[时空复杂度] 时间复杂度为O(n),空间复杂度为 O(n)。
Apprentissage recommandé : Tutoriel Python
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

