Maison >développement back-end >Tutoriel Python >Compréhension approfondie du traitement et de la visualisation des données Python
Compréhension approfondie du traitement et de la visualisation des données Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2022-03-21 17:43:432474parcourir
Cet article vous apporte des connaissances pertinentes sur python, qui introduit principalement les problèmes liés au traitement et à la visualisation des données, y compris l'utilisation préliminaire de NumPy, l'utilisation du package Matplotlib et l'affichage visuel des statistiques de données, etc. J'espère que cela aidera tout le monde.

Apprentissage recommandé : Tutoriel Python
1. Utilisation initiale de NumPy
Table est une représentation générale des données, mais elle est incompréhensible pour la machine, c'est-à-dire que ce sont des données méconnaissables, nous avons donc besoin d'Ajuster la forme du tableau.
Une représentation d'apprentissage automatique couramment utilisée est une matrice de données. 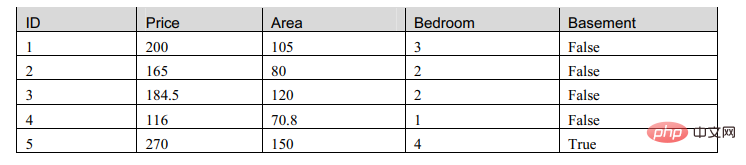
Nous avons examiné ce tableau et avons constaté qu'il existe deux types d'attributs dans la matrice, l'un est de type numérique et l'autre est de type booléen. Nous allons donc maintenant construire un modèle pour décrire cette table :
# 数据的矩阵化import numpy as np data = np.mat([[1,200,105,3,False],[2,165,80,2,False],[3,184.5,120,2,False], [4,116,70.8,1,False],[5,270,150,4,True]])row = 0for line in data: row += 1print( row )print(data.size)print(data)
La première ligne de code ici signifie introduire NumPy et le renommer en np. Dans la deuxième ligne, nous utilisons la méthode mat() dans NumPy pour créer une matrice de données, et row est la variable introduite pour calculer le nombre de lignes.
La taille ici signifie un tableau de 5*5. Vous pouvez voir les données en imprimant les données directement : 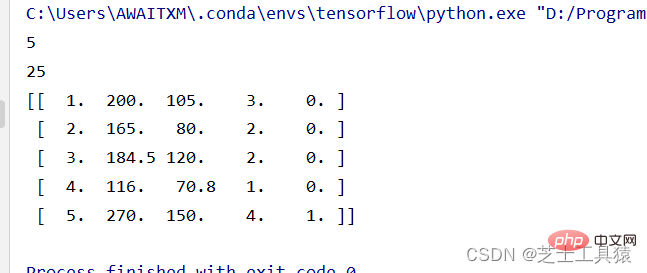
2. Utilisation du package Matplotlib – traitement graphique des données
Regardons le tableau du haut. Deuxième La colonne est. la différence entre les prix des logements. Il n'est pas facile de voir la différence intuitivement (car il n'y a que des chiffres), nous espérons donc la dessiner (La façon d'étudier les différences numériques et les anomalies est de dessiner la distribution des données) :
import numpy as npimport scipy.stats as statsimport pylab data = np.mat([[1,200,105,3,False],[2,165,80,2,False],[3,184.5,120,2,False], [4,116,70.8,1,False],[5,270,150,4,True]])coll = []for row in data: coll.append(row[0,1])stats.probplot(coll,plot=pylab)pylab.show()
Le résultat de ce code est de générer une image :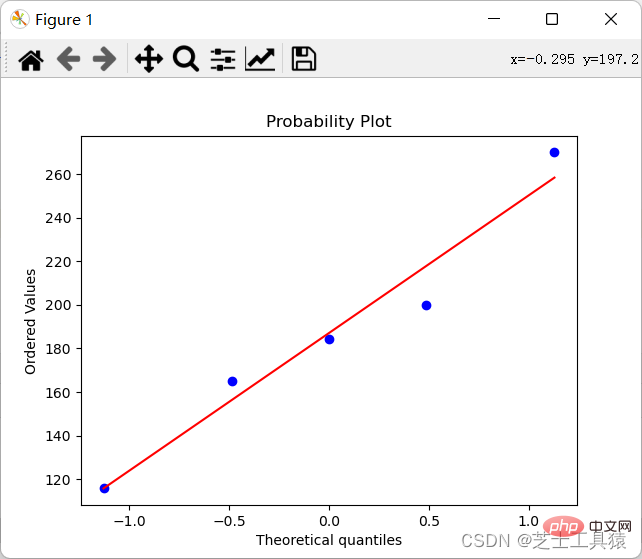
Pour que l'on puisse voir clairement la différence.
L'exigence d'un diagramme de coordonnées est d'afficher les valeurs spécifiques des données à travers différentes lignes et colonnes.
Bien sûr, nous pouvons également afficher le diagramme de coordonnées : 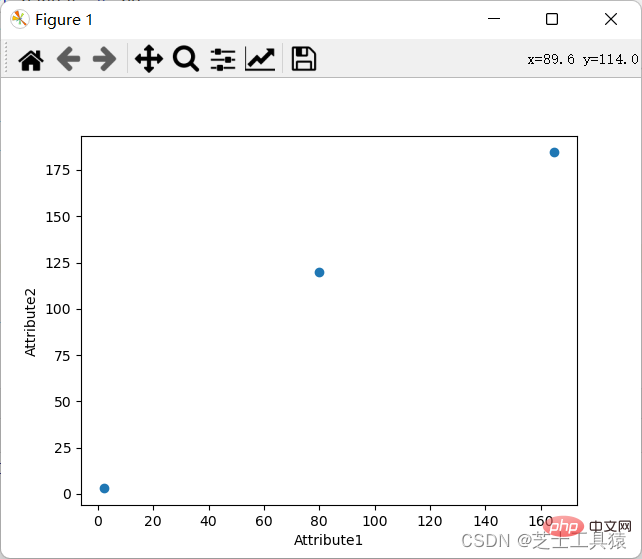
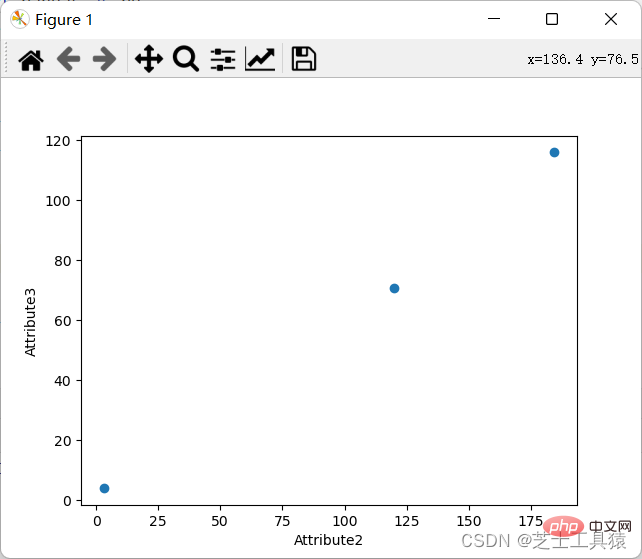
3. Méthode théorique du Deep Learning – calcul de similarité (peut être ignoré)
Il existe de nombreuses méthodes pour calculer la similarité. Nous choisissons les deux plus couramment utilisées, à savoir le calcul de similarité géodique euclidienne et de similarité cosinus.
1.Calcul de similarité basé sur la distance euclidienne
La distance euclidienne est utilisée pour représenter la vraie distance entre deux points dans l'espace tridimensionnel. Nous connaissons tous la formule, mais nous entendons rarement le nom : 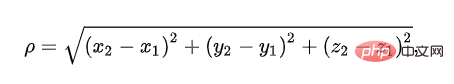
Voyons donc son application pratique :
Ce tableau représente les notes des éléments par 3 utilisateurs : 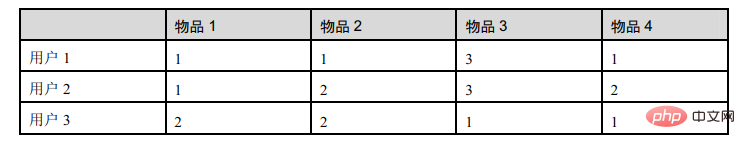
d12 indique la similitude entre l'utilisateur 1 et l'utilisateur 2 degrés, alors il y a : 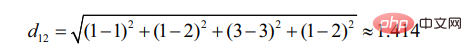
De même, d13 : 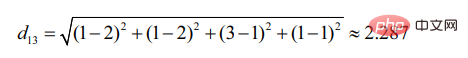
On voit que l'utilisateur 2 est plus similaire à l'utilisateur 1 (plus la distance est petite, plus la similitude est grande).
2. Calcul de similarité basé sur l'angle cosinus
Le point de départ du calcul de l'angle cosinus est la différence de l'angle inclus. 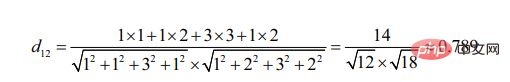
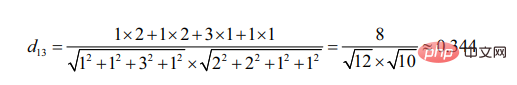
On peut voir que par rapport à l'utilisateur 3, l'utilisateur 2 est plus similaire à l'utilisateur 1 (plus les deux cibles sont similaires, plus l'angle formé par leurs segments de ligne est petit)
4. Affichage visuel de statistiques de données (basées sur les précipitations de la ville de Bozhou à titre d'exemple)
Quartiles de données
Les quartiles sont un type de quantile en statistique, c'est-à-dire que les données sont classées de petite à grande, puis divisées en quatre parties égales, en trois divisions Les données à la position du point sont les quartiles.
Premier quartile (Q1), également appelé quartile inférieur;
Deuxième quartile (Q1), également appelé médiane;
L'écart entre le troisième quartile et le premier quartile est également appelé écart inter-quartile (IQR).
若n为项数,则:
Q1的位置 = (n+1)*0.25
Q2的位置 = (n+1)*0.50
Q3的位置 = (n+1)*0.75
四分位示例:
关于这个rain.csv,有需要的可以私我要文件,我使用的是亳州市2010-2019年的月份降水情况。
from pylab import *import pandas as pdimport matplotlib.pyplot as plot
filepath = ("C:\\Users\\AWAITXM\\Desktop\\rain.csv")# "C:\Users\AWAITXM\Desktop\rain.csv"dataFile = pd.read_csv(filepath)summary = dataFile.describe()print(summary)array = dataFile.iloc[:,:].values
boxplot(array)plot.xlabel("year")plot.ylabel("rain")show()
以下是plot运行结果: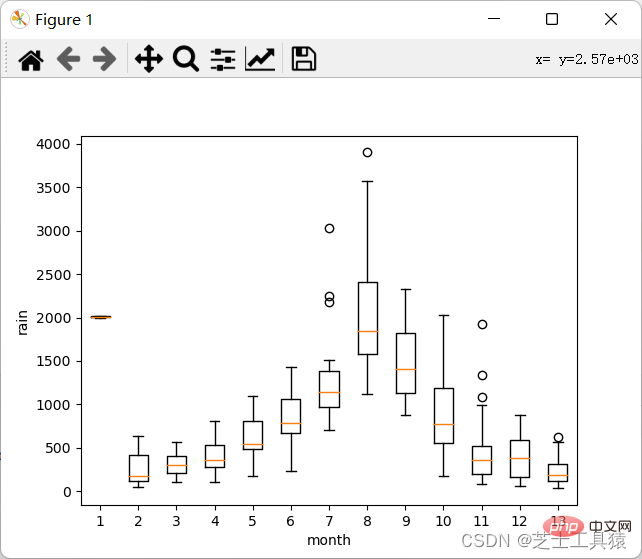
这个是pandas的运行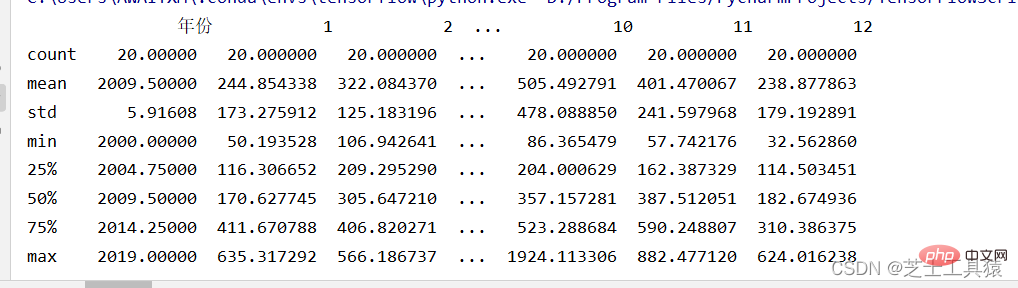
这里就可以很清晰的看出来数据的波动范围。
可以看出,不同月份的降水量有很大差距,8月最多,1-4月和10-12月最少。
那么每月的降水增减程度如何比较?
from pylab import *import pandas as pdimport matplotlib.pyplot as plot
filepath = ("C:\\Users\\AWAITXM\\Desktop\\rain.csv")# "C:\Users\AWAITXM\Desktop\rain.csv"dataFile = pd.read_csv(filepath)summary = dataFile.describe()minRings = -1maxRings = 99nrows = 11for i in range(nrows):
dataRow = dataFile.iloc[i,1:13]
labelColor = ( (dataFile.iloc[i,12] - minRings ) / (maxRings - minRings) )
dataRow.plot(color = plot.cm.RdYlBu(labelColor),alpha = 0.5)plot.xlabel("Attribute")plot.ylabel(("Score"))show()
结果如图: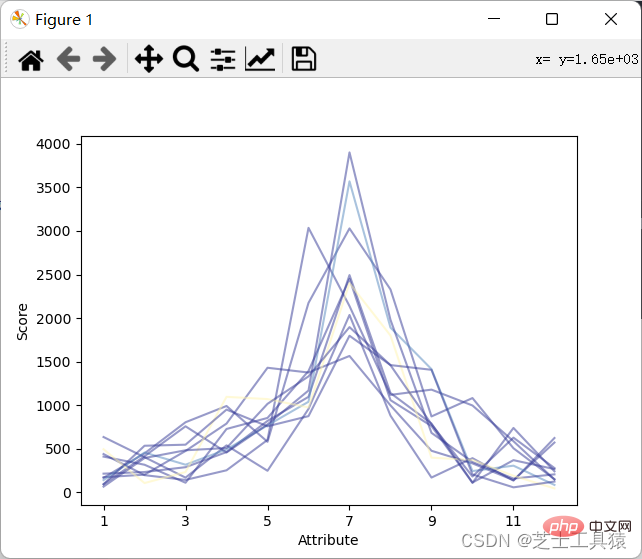
可以看出来降水月份并不规律的上涨或下跌。
那么每月降水是否相关?
from pylab import *import pandas as pdimport matplotlib.pyplot as plot
filepath = ("C:\\Users\\AWAITXM\\Desktop\\rain.csv")# "C:\Users\AWAITXM\Desktop\rain.csv"dataFile = pd.read_csv(filepath)summary = dataFile.describe()corMat = pd.DataFrame(dataFile.iloc[1:20,1:20].corr())plot.pcolor(corMat)plot.show()
结果如图: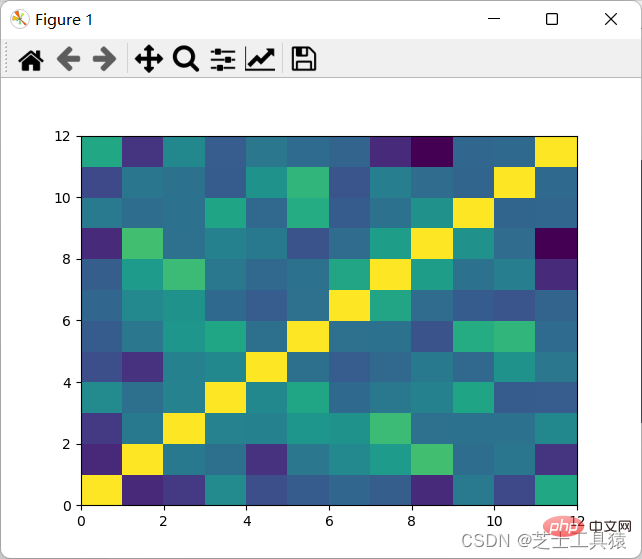
可以看出,颜色分布十分均匀,表示没有多大的相关性,因此可以认为每月的降水是独立行为。
今天就记录到这里了,我们下次再见!希望本文章对你也有所帮助。
推荐学习:python学习教程
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

