Explication détaillée de la traversée de l'arbre binaire et des méthodes d'opérations logiques

Tout d'abord, nous devons encore expliquer que le contenu principal que nous étudions est celui des arbres binaires, car les arbres binaires sont l'application la plus typique des arbres. Qu'il s'agisse d'un examen ou d'un entretien, c'est un incontournable et un incontournable. contenu.

Tout d'abord, avant d'apprendre le fonctionnement de l'arbre, il faut d'abord comprendre que le cœur du fonctionnement de l'arbre est la « traversée ». Pourquoi tu dis ça ? Contrairement aux piles et aux files d’attente, la structure arborescente n’est en réalité plus unidimensionnelle. Elle comporte des branches, des angles différents et, plus important encore, elle comporte le concept de hiérarchie.

Les objets dans un espace unidimensionnel sont nos « lignes » communes, qui n'ont qu'une longueur mais pas de hauteur, et cette longueur est sa seule dimension. Les piles et les files d'attente sont évidemment unidimensionnelles. L'arbre est différent en raison du concept de hiérarchie, il a une « hauteur », c'est-à-dire qu'il a été amélioré en un concept bidimensionnel. Tout comme l'ensemble de noms introduits dans l'article précédent, il existe la notion de « hauteur (profondeur) d'un arbre ».

Après avoir pu parcourir un arbre, nous pouvons ajouter, supprimer, modifier et d'autres opérations sur les nœuds de l'arbre en fonction du parcours. Ces opérations logiques de base sont toutes basées sur le parcours. leurs opérations logiques ne commencent-elles pas également par le parcours ? Qu'il s'agisse de sauter ou d'entrer dans la pile ou de sortir ou de mettre en file d'attente, nous sommes tous basés sur une règle de parcours fixe (FILO, FIFO).

Pour les choses bidimensionnelles, comment les parcourir est un point clé. Nous n'avons besoin que de parcourir la structure de données unidimensionnelle de manière séquentielle, mais les résultats des données bidimensionnelles ne peuvent pas simplement être parcourus un par un dans l'ordre, car il existe des relations hiérarchiques entre les nœuds, nous devons donc considérer le courant Si le nœud n'a pas nœuds enfants, que devons-nous faire de notre opération de traversée ?

Heureusement, nous apprenons ces connaissances en nous tenant sur les épaules de géants. De nombreux seniors ont résumé pour nous quelques méthodes très simples de traversée d’arbres. Dans quelle mesure sont-elles simples ? Commençons par sortir du sujet, voyons comment construire un arbre, qui est l'arbre binaire que nous avons montré dans l'article précédent.

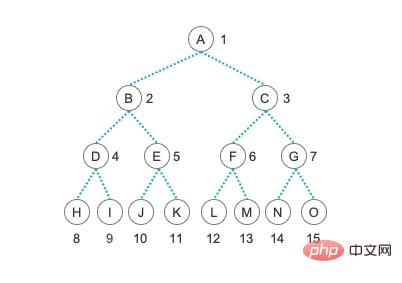
Structure de stockage en chaîne des arbres binaires

Utiliser le stockage en chaîne pour stocker les arbres binaires est très simple et très visuel. Mes amis, veuillez mettre de côté vos questions sur le stockage séquentiel des arbres binaires, car nous l'expliquerons dans le prochain article. Quand utiliser le stockage séquentiel.

class BiTree
{
    public $data;
    public $lChild;
    public $rChild;
}

En fait, dans le stockage en chaîne, on utilise les nœuds un par un pour sauver l'arbre. Chaque nœud d'arbre binaire possède un champ de données, qui est l'attribut data. Les deux autres attributs peuvent être considérés comme deux pointeurs fourchus, à savoir le nœud enfant gauche lChild et le nœud enfant droit rChild de ce nœud.

En comparant la pile et la file d'attente, nous venons de remplacer le nœud suivant par les nœuds enfants gauche et droit. En substance, ce n'est pas très différent de la pile et de la file d'attente. Pour parler franchement, du point de vue de la structure des données, nous utilisons toujours le stockage unidimensionnel pour représenter des concepts bidimensionnels, et la transformation de ce concept nous oblige à partir du point de vue de la compréhension conceptuelle.

Construction d'un arbre binaire

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i])) {
        return null;
    }
    $t = new BiTree();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

Avec une méthode aussi simple, nous pouvons compléter l'établissement d'un arbre binaire enchaîné. Mes amis, regardez attentivement, cette simple opération de construction d'arbre contient en fait beaucoup de mystères :

• Nous utilisons un tableau pour représenter chaque nœud de l'arbre dans l'ordre, comme entrer A, B, C, D, E dans l'ordre ... (Nous les reverrons dans le stockage séquentiel de l'arbre)

• Le contenu attribué est les données de l'indice $i actuel. Notez que nous avons effectué une opération récursive lors de l'attribution de valeurs à gauche et. bons enfants

• Lors de l'apprentissage de la pile, nous avons appris que la "récursivité" est une opération de type pile. Par conséquent, dans ce code, nous construisons l'arbre sous la forme d'une pile

• Remarquez qu'à chaque fois je 2. et moi 2 + 1, non ? Veuillez examiner la propriété 5 des arbres binaires

Enfin, nous testons si cette méthode peut réussir à construire une structure arborescente liée.

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];

$tree = CreateBiTree($treeList, 1);
print_r($tree);

// BiTree Object
// (
//     [data] => A
//     [lChild] => BiTree Object
//         (
//             [data] => B
//             [lChild] => BiTree Object
//                 (
//                     [data] => D
//                     [lChild] => BiTree Object
//                         (
//                             [data] => H
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => I
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//             [rChild] => BiTree Object
//                 (
//                     [data] => E
//                     [lChild] => BiTree Object
//                         (
//                             [data] => J
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => K
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//         )

//     [rChild] => BiTree Object
//         (
//             [data] => C
//             [lChild] => BiTree Object
//                 (
//                     [data] => F
//                     [lChild] => BiTree Object
//                         (
//                             [data] => L
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => M
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//             [rChild] => BiTree Object
//                 (
//                     [data] => G
//                     [lChild] => BiTree Object
//                         (
//                             [data] => N
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => O
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//         )

// )

Le contenu imprimé doit être très clair, non ? Le nœud A a deux nœuds enfants gauche et droit, à savoir B et C, le nœud B a deux nœuds enfants gauche et droit, respectivement D et E, et ainsi de suite. La structure finale est exactement la même que la structure de notre arbre binaire ci-dessus. Ici, nous devons également faire attention au fait que pour le tableau transmis, nous donnons le premier élément, c'est-à-dire les données avec un indice 0, vide, et construisons l'arborescence à partir du deuxième élément, qui est l'élément avec un indice 1. Il s'agit également de pouvoir utiliser intuitivement et commodément la propriété 5 de l'arbre binaire pour construire rapidement cet arbre.

二叉树的遍历

说完二叉树的建树了，其实我们就已经接触到了一种二叉树的遍历形式。注意看我们建树方法中的代码，我们是先给结点的 data 赋值，然后建立这个结点的左、右孩子结点，并为它们赋值后再继续使用同样的操作一路建立完成所有的结点。现在，我们将这个操作反过来，不是建立结点，而是读取这些结点的内容，先读取结点的内容，然后再读取这个结点左右孩子结点的内容，这就是“先序遍历”。

先序遍历

/**
 * 前序遍历
 */
function PreOrderTraverse(?BiTree $t)
{
    if ($t) {
        echo $t->data, ',';
        PreOrderTraverse($t->lChild);
        PreOrderTraverse($t->rChild);
    }
}

PreOrderTraverse($tree);

// A,B,D,H,I,E,J,K,C,F,L,M,G,N,O,

是不是很神奇？就连建树我们竟然也使用的是同一种遍历的方法，可以看出对于二叉树这种复杂的数据结构来说，遍历的重要作用了吧。

大家可以看一个遍历读取出来的结点顺序，貌似和我们输入的顺序不一样呀！没错，先序遍历是通过递归，先按一个方向走到底，当这个结点没有子结点之后，通过递归栈的特性再向上弹出。并且在遍历孩子结点之前先输出当前这个结点的内容。注意，这一句话很重要！所以我们的顺序就是 A,B,D,H ，当 H 没有子结点之后，我们就回到父结点 D 再进入它的右子结点 I ，具体顺序可以参考下图：

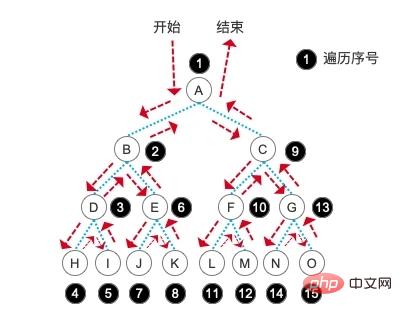
我们代码中的先序遍历和先序建树的结点顺序是完全不一样的，这一点也是要搞清楚的。建树的过程我们根据二叉树的 性质5 直接为它指定了数据下标。而在遍历过程中则是一个结点一个结点的去扫描遍历整颗树的。

中序遍历

顾名思义，中序遍历其实就是在遍历完左孩子结点之后再输出当前这个结点的内容，所以我们只需要微调先序遍历的代码即可。

/**
 * 中序遍历
 */
function InOrderTraverse(?BiTree $t)
{
    if ($t) {
        InOrderTraverse($t->lChild);
        echo $t->data, ',';
        InOrderTraverse($t->rChild);
    }
}

InOrderTraverse($tree);

// H,D,I,B,J,E,K,A,L,F,M,C,N,G,O,

中序遍历的步骤就是我们会直接先走到最左边的子结点，当遇到最后一个结点时，输出内容，也就是图中的 H 结点，接着回到它的父结点 D 结点，这时根据中序的原理输出 D ，再进入它的右孩子结点并输出 I 。

D 结点的子树及它本身遍历完成后，返回 D 结点的上级结点 B 结点，输出 B ，然后进入 B 结点的右孩子结点 E 。再次进入到 E 的最左孩子结点 J ，然后参考 D 结点的遍历形式完成整颗树的遍历。具体顺序参考下图：

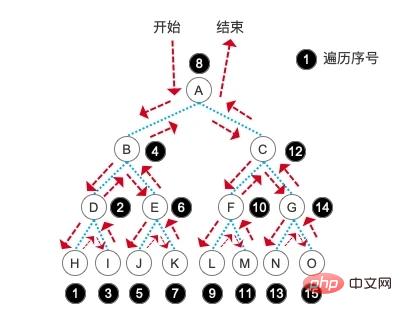
后序遍历

在学习了先序和中序之后，从名字就可以看出来后序就是在遍历完一个结点的左右孩子之后最后输出这个结点的内容，代码当然也是简单地微调一下就可以了。

/**
 * 后序遍历
 */
function PostOrderTraverse(?BiTree $t)
{
    if ($t) {
        PostOrderTraverse($t->lChild);
        PostOrderTraverse($t->rChild);
        echo $t->data, ',';
    }
}

PostOrderTraverse($tree);

// H,I,D,J,K,E,B,L,M,F,N,O,G,C,A,

具体原理就不详细说明了，相信在学习了先序和中序之后，你一定能马上想明白后序遍历到底是什么意思了。直接上图：

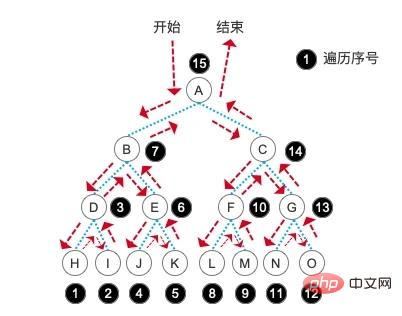
层序遍历

最后，我们要讲的就是层序遍历。既然有“层”这个关键字了，相信大家马上就能联想到，是不是一层一层地去遍历啊！没错，层序遍历就是这个意思，我们按照树的层次，一层一层地输出相应的结点信息。需要注意的，在这里我们会用到队列，而不是栈了。

/**
 * 层序遍历
 */
$q = InitLinkQueue();
function LevelOrderTraverse(?BiTree $t)
{
    global $q;
    if (!$t) {
        return;
    }

    EnLinkQueue($q, $t);
    $node = $q;
    while ($node) {
        $node = DeLinkQueue($q);
        if ($node->lChild) {
            EnLinkQueue($q, $node->lChild);
        }
        if ($node->rChild) {
            EnLinkQueue($q, $node->rChild);
        }
        echo $node->data, ',';
    }
}

LevelOrderTraverse($tree);

// A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,

InitLinkQueue() EnLinkQueue() 、 EnLinkQueue() 这些都是我们之前学习队列的时候所写的对于队列的逻辑操作方法。是不是很开心呀，之前的知识又用上了。层序遍历的核心思想就是运用队列的概念，遇到一个结点，就把这个结点入队，然后判断它是否有子结点，然后相继把子结点入队。

每遍历一个结点，就把队首的结点出队，这样就完成了按树的层次遍历的能力。文字说明还是太抽象，我们还是通过图片来展示这一过程：

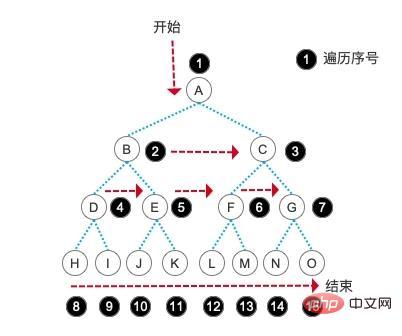
大家有没有发现，层序遍历的输出结果就和我们建树时的数组顺序完全相同了。很好玩吧，所以说代码的世界总是有无穷的乐趣等着我们去发现哦！

总结

今天的内容有没有懵圈？如果懵圈了就多找资料好好研究一下，先序、中序、后序都是利用栈来进行树的结点遍历的，而层序遍历则是利用了队列。一环套一环呀，前面学习的内容都派上用场了吧！不过这只是个开始，在学习图的时候，我们会在深度遍历和广度遍历中再次看到栈和队列的身影，它们可都是亲戚哦。

这四种遍历方式在考试和面试中也是经常出现的，不管是它们的原理还是画图或者是根据图形来写出各种遍历的顺序，都是非常常见的考核内容，所以大家在这篇文章入门的基础上还是要更加深入的去根据一些教材来深入的理解这几种遍历，熟练的掌握它们。

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.2二叉树的遍历及逻辑操作.php

推荐学习：php视频教程

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!