Découvrez les arbres et les arbres binaires en trois minutes

Dans le domaine informatique, les [dossiers] que nous traitons quotidiennement et les données que nous stockons dans les bases de données sont toutes des applications typiques des arbres. Aujourd'hui, nous allons découvrir les définitions plus théoriques des arbres et des arbres binaires ainsi que certains de leurs attributs et caractéristiques.

Arbre

À partir des exemples ci-dessus dans la vie réelle, nous pouvons voir que la structure arborescente peut résumer certaines de ses caractéristiques.

Tree (Tree) est un ensemble fini de N (N>0) nœuds. C'est soit un arbre vide (N=0), soit un arbre T non vide.

Dans cette définition, nous devons clarifier deux problèmes : premièrement, l'arbre doit avoir des nœuds, et deuxièmement, selon le nombre de nœuds, il peut être divisé en deux types : les arbres vides et les arbres non vides. Mais ce n’est que la définition la plus élémentaire, elle possède certaines propriétés.

Il n'y a et il n'y a qu'un seul nœud appelé racine.

En d'autres termes, cet arbre doit s'étendre à partir d'un certain nœud, qui est comme la racine de l'arbre. À partir de là, commencent à se ramifier vers l’extérieur.

À l'exception du nœud racine, les nœuds restants peuvent être divisés en m ( m > 0 ) ensembles finis disjoints T1, T2..., Tm. Chaque ensemble lui-même est un arbre et est appelé sous-arbre (SubTree).

Ce paragraphe n'est peut-être pas facile à comprendre. En fait, pour parler franchement, chaque nœud n'a qu'un seul nœud supérieur et ne peut pas avoir plusieurs nœuds supérieurs. De la même manière, il ne peut y avoir de connexion entre les nœuds horizontaux, mais il peut y avoir plusieurs nœuds subordonnés.

Pour la définition d'arbre, on peut regarder l'image ci-dessous.

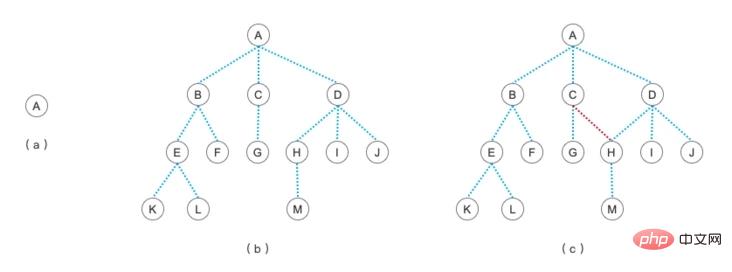
L'image ci-dessus répertorie brièvement à quoi ressemblent les arbres standards et les arbres non standards. Parmi eux :

• (a) est un arbre avec un seul nœud racine Tant qu'il y a un nœud, cela peut être appelé une structure arborescente

• (b) , est une structure arborescente standard

• .

  (c), notez qu'il y a une ligne de connexion entre ses nœuds C et H. Ce n'est pas un arbre. Un nœud ne peut être appelé un arbre que s'il a un nœud supérieur. [ Photo]

Termes liés aux arbres

Par rapport au push (into) et au pop out de la pile, ainsi qu'à la mise en file d'attente et à la sortie de la file d'attente, les termes liés à l'arbre sont beaucoup plus compliqués. Quoi qu’il en soit, vous devez d’abord vous souvenir de ces termes, sinon la terminologie utilisée dans ce qui sera discuté plus tard ne fera que vous rendre encore plus confus. Mais peu importe si nous ne parvenons pas à nous en souvenir pour le moment. Nous pouvons d’abord avoir une impression approximative, puis revenir la revoir lorsque nous la rencontrerons plus tard dans le processus d’apprentissage. Cela rendra l’impression plus profonde.

• Nœud : Un nœud peut contenir un ensemble de données, ou une branche pointant vers d'autres nœuds. Il peut être considéré comme l'endroit où se ramifient les branches (b) A, B, C, D, E, etc. dans la figure Ce sont les degrés des nœuds

• : Le nombre de sous-arbres appartenant à un nœud est appelé le degré du nœud. En fait, c'est le degré du nombre de sous-nœuds subordonnés qu'il possède (b). Dans la figure, le degré du nœud C est 1 et le degré du nœud D est 3

• Le degré de l'arbre : la valeur maximale du degré de chaque nœud dans l'arbre est le degré du plus grand nombre de nœuds enfants, qui est le degré de l'arbre, (b) Le degré de cet arbre sur la photo est 3

• Feuilles : nœuds de degré 0, c'est-à-dire nœuds sans nœuds enfants, (b) K, L, F, G , M, sur l'image I et J sont les nœuds feuilles de cet arbre

• Parents et enfants : les nœuds enfants d'un nœud sont ses enfants ; pour ces nœuds enfants, le nœud actuel est son parent, ( b) Dans sur l'image, les enfants de D sont H, I et J, et les parents de H, I et J sont D

• Niveau : en comptant à partir du nœud racine, le nœud racine est le premier niveau, et les enfants de la racine sont le deuxième niveau, et ainsi de suite, (b) le niveau du nœud G dans l'image est 3, (a) tous les niveaux de l'image sont seulement 1

• La profondeur (hauteur) du arbre : le niveau maximum actuel de l'arbre, Évidemment, la profondeur du graphique (b) est de 4

• Frères, ancêtres et descendants : les nœuds frères sont les parents de ces nœuds sont les mêmes nœuds ancêtres ; nœud racine vers un nœud spécifié Tous les nœuds passant sur la route ; les descendants sont tous des nœuds sur la route commençant à partir d'un certain nœud et atteignant le nœud cible. (b) Sur la figure, E et F sont frères, les ancêtres de E sont A et B, et les descendants de E sont K ou L

• cousins : tous les nœuds sont au même niveau mais avec des parents différents. Ils sont tous cousins. photo (b), les cousins ​​​​de G sont E et F. De plus, H, I et J sont aussi ses cousins

Arbre binaire

Pour l'arbre Après avoir une certaine compréhension du concept, approfondissons apprenez un autre concept, qui est également la forme arborescente la plus importante dans les structures de données et les algorithmes : les arbres binaires.

De manière générale, la forme de l'arborescence peut changer constamment. Par exemple, un nœud peut avoir 3 nœuds enfants, tandis qu'un autre nœud peut avoir 300 nœuds enfants. Un tel arbre sans aucune règle sera en fait très difficile à exploiter, et la définition d'un arbre binaire est beaucoup plus simple. En plus des propriétés d'un arbre, il a également un contenu supplémentaire : chaque nœud d'un arbre binaire en a au plus. deux nœuds enfants. , c'est-à-dire que le degré de l'arbre binaire entier doit être 2 et que le degré de tous les nœuds ne dépassera pas 2. Quant aux raisons pour lesquelles les arbres binaires sont faciles à utiliser, nous l'expliquerons en détail dans les propriétés des arbres binaires dans la section suivante. Toutes les structures arborescentes peuvent être converties en arbres binaires grâce à certaines déformations régulières.

Nous utilisons également un diagramme pour montrer ce qu'est un arbre binaire.

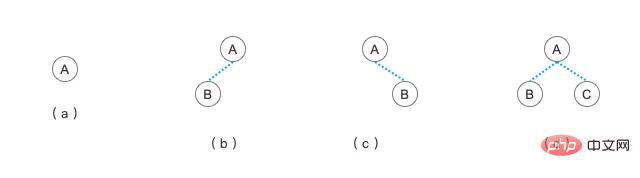
Dans un arbre binaire, le nœud enfant gauche et ses descendants peuvent être considérés comme le sous-arbre gauche du nœud actuel. Le nœud droit et ses nœuds descendants peuvent également être considérés comme le sous-arbre droit du nœud actuel. Selon les nœuds enfants du nœud, il existe plusieurs formes d'arbre binaire, comme le montre la figure ci-dessus.

• (a) Un arbre est un arbre avec un seul nœud, on peut aussi dire qu'il s'agit d'un arbre binaire avec un seul nœud

• (b) Un arbre est un arbre binaire avec un seul nœud gauche

• (c) L'arbre est un arbre binaire avec un seul nœud droit

• (d) L'arbre est un arbre binaire avec deux nœuds gauche et droit

Propriétés des arbres binaires

Propriété 1 : Au i-ième niveau de l'arbre binaire Il y a au plus 2i-1 nœuds (i >= 1)

Propriété 2 : Un arbre binaire de profondeur k a au plus 2k - 1 nœuds (k >= 1)

Propriété 3 : Pour tout arbre binaire T, si le nombre de ses nœuds terminaux est n0 et le nombre de nœuds de degré 2 est n2, alors n0 = n2 + 1

Propriété 4 : La profondeur d'un binaire complet arbre à n nœuds est log2n + 1

Propriété 5 : Si les nœuds d'un arbre binaire complet à n nœuds (sa profondeur est log2n + 1) sont numérotés dans l'ordre des couches (du premier niveau au log2n + 1ème niveau, chacun niveau de gauche à droite), alors pour tout nœud A i (1

1. Si i = 1, alors le nœud i est la racine d'un arbre binaire et n'a pas de parents ; si i > 1, alors ses parents sont des nœuds Point i / 2
2. Si 2i > n , alors le nœud i n'a plus d'enfant (le nœud i est un nœud feuille sinon son enfant gauche est le nœud 2i
3. ) ; Si 2i + 1 > n , alors le nœud i n'a pas de bon enfant ; sinon son bon enfant est le nœud 2i + 1

Nous n'entrerons pas dans les détails des preuves mathématiques des cinq propriétés des arbres binaires ci-dessus. le but de notre série d'articles est également d'utiliser des exemples simples. Laissez tout le monde apprendre l'essence des structures de données et des algorithmes, au lieu d'utiliser simplement et grossièrement des formules mathématiques pour dériver des preuves, nous pouvons alors simplement les compter sur l'image.

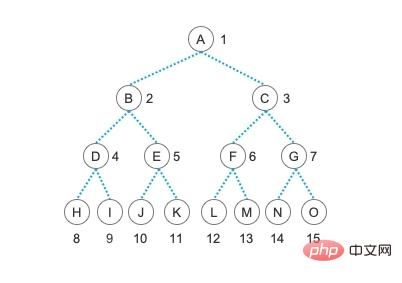
• Pour la propriété 1, selon la formule, notre arbre binaire actuel ne peut avoir qu'un maximum de 23-1 nœuds au troisième niveau, soit 4 nœuds. Il ne peut y avoir qu'un maximum de 24-1 sur la 4ème couche, soit 23 = 8 nœuds

• Pour la propriété 2, la profondeur de l'arbre dans l'image actuelle est de 4, c'est-à-dire qu'il y a un maximum de 24 - 1 = 15 Si le nœud

• a la propriété 3, on compte d'abord le nombre de nœuds de degré 2. Dans cette figure, il y a 7 nœuds de degré 2, soit A, B, C, D, E , F, G, les nœuds de la quatrième couche n'ont pas de nœuds enfants, c'est-à-dire qu'ils sont tous à 0 degré, également appelés nœuds terminaux (nœuds feuilles). Le nombre de ces nœuds est de 8 au total. Maintenant n2 = 7, selon la formule de propriété, nous pouvons obtenir n0 = n2 + 1 = 7 + 1 = 8

• Le nombre de nœuds dans le graphique est 15, en appliquant la formule de la propriété 4, nous pouvons obtenir log2n + 1 = log215 + 1 = 3,91 (arrondi à l'inférieur) + 1 = 3 + 1 = 4, la profondeur de l'arbre actuel est de 4, la propriété 4 et la propriété 2 peuvent être considérées comme complémentaires

• Pour la propriété 5, veuillez noter Pour le numéro sur le bord de chaque nœud, nous sélectionnons le nœud E comme exemple. Le nœud E est actuellement 5, donc ses parents sont 5/2 = 2 (arrondi à l'inférieur) ; l'enfant gauche de E est 2i, c'est-à-dire 2*5=10, et l'enfant droit de E est 2i + 1, soit est 2*5+1 = 11 ; la définition de la propriété 5 est plus abstraite, et elle utilise des nœuds feuilles pour illustrer, et vise l'ensemble de l'arbre binaire, mais en fait la signification est la même que celle que nous expliquons ici, Vous peut le vérifier avec d’autres nœuds. La propriété 5 est très importante pour l’utilisation de structures séquentielles pour stocker des arbres binaires dont nous parlerons plus tard !

Assurez-vous de maîtriser et de vous souvenir de ces cinq propriétés des arbres binaires et de leurs significations, car dans les études ultérieures, qu'il s'agisse de l'ordre des arbres binaires, des structures de stockage enchaînées ou de la traversée des arbres binaires, vous pourriez tomber sur contact avec eux. contenu dans les cinq propriétés. On peut dire qu'ils constituent l'âme la plus fondamentale de l'apprentissage des arbres binaires.

Forêt

Enfin, comprenons brièvement ce qu'est la « forêt ». Plusieurs arbres réunis forment une « forêt ». Tout comme le diagramme explicatif de l'arbre binaire ci-dessus, (a) (b) (c) (d) sont assemblés et vus dans leur ensemble, c'est une « forêt », et dans cette « forêt » il y a (a) (b) (c) (d) ces quatre arbres.

Il n'y a aucun lien entre les arbres de la forêt. Si nous voulons exploiter ou traverser une forêt, nous transformons souvent la forêt en arbre. Les algorithmes et les étapes spécifiques ne sont pas au centre de notre étude, donc tout le monde peut les comprendre. Les étudiants qui souhaitent étudier en profondeur peuvent rechercher du contenu pertinent ou consulter des manuels pertinents.

Résumé

En passant de la pile et de la file d'attente derrière l'arbre, avez-vous soudain l'impression d'avoir fait un grand pas ? Un peu confus ? Peu importe, le contenu d'aujourd'hui est en fait un contenu théorique de base. Si vous pouvez le comprendre, comprenez-le. Si vous ne le comprenez pas, continuez à étudier et revenez ensuite examiner ces concepts aujourd'hui.

Apprendre n'implique pas de répéter constamment le processus de progrès. Bien sûr, tout doit être basé sur la base. Après avoir compris la structure des données des arbres et quelques algorithmes de parcours simples, revenez pour comprendre ces concepts en profondeur et les mémoriser. Je pense que les questions liées aux arbres dans les entretiens généraux seront hors de question. Travaillons dur ensemble !

Apprentissage recommandé : Tutoriel vidéo php

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!