Comment le tri topologique est-il trié ?

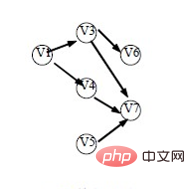
Méthode : 1. Trouver un nœud dans le graphique avec un degré en 0, supprimer ce nœud du graphique et l'ajouter à la séquence E ; 2. Supprimer toutes les arêtes associées du nœud trouvé en 1 du graphique ; Supprimer ; 3. Répétez les étapes 1 et 2 jusqu'à ce que tous les nœuds du graphique soient supprimés ou qu'un nœud avec un degré entrant de 0 ne soit pas trouvé.

L'environnement d'exploitation de ce tutoriel : système Windows 7, ordinateur Dell G3.

1. Trouvez un nœud dans le graphique avec un degré en 0, supprimez ce nœud du graphique et ajoutez-le à la séquence E

2. Supprimez toutes les arêtes associées du nœud trouvé en 1 du graphique

3. Répétez 1 et 2 jusqu'à ce que tous les nœuds du graphique soient supprimés ou qu'un nœud avec un degré entrant de 0 ne puisse pas être trouvé

Si le nombre de nœuds dans le graphique est 0 à ce moment, la séquence topologique est trouvé. Si cela Lorsque le nombre de nœuds dans le graphique n'est pas 0, cela signifie qu'il y a un cycle dans le graphique et que le tri topologique ne peut pas être effectué.

Informations étendues :

Pour effectuer un tri topologique sur un graphe acyclique dirigé (DAG en abrégé), G consiste à organiser tous les sommets de G dans une séquence linéaire telle que toute paire de sommets u et v dans le graphe, si edge ∈E(G), alors u apparaît avant v dans la séquence linéaire. Habituellement, une telle séquence linéaire est appelée séquence qui satisfait l’ordre topologique, ou est appelée séquence topologique. En termes simples, d'un ordre partiel sur un certain ensemble à un ordre total sur l'ensemble, cette opération est appelée tri topologique.

Étapes d'exécution

L'algorithme de tri topologique qui construit une séquence topologique à partir du réseau AOV effectue principalement les deux étapes suivantes dans une boucle jusqu'à ce qu'il n'y ait plus de sommet avec un degré entrant de 0.

(1) Sélectionnez un sommet avec un degré en 0 et affichez-le

(2) Supprimez ce sommet et toutes les arêtes sortantes du réseau ;

Après la fin de la boucle, si le nombre de sommets en sortie est inférieur au nombre de sommets dans le réseau, les informations de « boucle » seront sorties, sinon la séquence de sommets en sortie est une séquence topologique.

Pour plus de connaissances liées à l'informatique, veuillez visiter la rubrique FAQ !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!