Maison >Problème commun >Quelle est la différence entre les systèmes variables dans le temps et les systèmes invariants dans le temps ?
Quelle est la différence entre les systèmes variables dans le temps et les systèmes invariants dans le temps ?
- 青灯夜游original
- 2020-10-16 15:16:5445347parcourir
La différence entre les systèmes variables dans le temps et les systèmes invariants dans le temps : une ou plusieurs valeurs de paramètres dans un système variable dans le temps changent avec le temps, de sorte que les caractéristiques entières changent également avec le temps tandis que les propriétés d'un système varient dans le temps. Les systèmes invariants dans le temps ne changent pas avec le temps. Le comportement de la réponse du système dépend uniquement du comportement du signal d'entrée et des caractéristiques du système, et n'a rien à voir avec le moment où le signal d'entrée est appliqué.

L'environnement d'exploitation de ce tutoriel : système Windows 7, ordinateur Dell G3.
Selon que le système contient ou non des composants dont les paramètres changent avec le temps, les systèmes de contrôle automatique peuvent être divisés en deux catégories : les systèmes à variation temporelle et les systèmes stables.
Un système stationnaire est également appelé système invariant dans le temps. Ses caractéristiques sont : Les propriétés propres du système (propriétés essentielles de l'objet étudié telles que la masse, le moment d'inertie). , etc.)Ne change pas dans le temps. Plus précisément, le comportement de la réponse du système dépend uniquement du comportement du signal d'entrée et des caractéristiques du système, et n'a rien à voir avec le moment où le signal d'entrée est appliqué, c'est-à-dire si l'entrée u(t) produit. la sortie y(t), puis lorsque l'entrée est retardée. Après que τ soit appliqué au système, la sortie produite par u(t-τ) est y(t-τ).
Un système stationnaire est aussi appelé système invariant dans le temps
C'est-à-dire : les propriétés de le système ne change pas avec le temps et ne change pas. Plus précisément, le comportement de la réponse du système dépend uniquement du comportement du signal d'entrée et des caractéristiques du système, et n'a rien à voir avec le moment où le signal d'entrée est appliqué. C'est-à-dire que je saisis u au temps t1 et la sortie est y Ensuite, je saisis u au temps t2 et la valeur de sortie est toujours y
Time. -système variable
Un système dans lequel une ou plusieurs valeurs de paramètre changent avec le temps, et donc toutes les caractéristiques changent également avec le temps.
Une fusée est un exemple typique de système variable dans le temps. Pendant le vol, sa masse diminue avec le temps en raison de la consommation de carburant ; un autre exemple courant est un manipulateur qui, lorsqu'il est en mouvement ; Le moment d'inertie de chaque articulation autour de l'axe correspondant est une fonction complexe avec le temps comme variable indépendante.
Un système invariant dans le temps est un système dont la sortie ne change pas directement avec le temps.
Si le signal d'entrée  produit une sortie y(t), alors pour tout retard, l'entrée
produit une sortie y(t), alors pour tout retard, l'entrée  obtiendra une sortie avec le même temps retard
obtiendra une sortie avec le même temps retard  .
.
Cette propriété peut être satisfaite si la fonction de transfert du système n'est pas fonction du temps. Cette fonctionnalité peut également être décrite en termes schématiques
Si un système est invariant dans le temps, alors le schéma fonctionnel du système et le schéma fonctionnel à tout moment sont interchangeables.
Pour montrer comment déterminer si un système est invariant dans le temps, examinons deux systèmes :
Système A :

Système B :

Puisque le système A dépend explicitement de t en plus de x(t) et y(t), c'est un système variable dans le temps, tandis que le système B ne dépend pas explicitement du temps t C'est donc invariant dans le temps.
Analyse mathématique :
Supposons que l'entrée d'un certain système soit u(t) et que la sortie correspondante soit y(t).
Lorsque l'entrée est retardée de τ, c'est-à-dire lorsque l'entrée est u(t-τ), si la sortie est également retardée de τ en conséquence, c'est-à-dire que la sortie est y(t-τ), Alors ce système est un système stable.
C'est-à-dire que lorsque le signal d'entrée u(t) est d'abord décalé dans le temps τ vers u(t-τ), puis la transformation du système H[without] est effectuée pour obtenir la valeur H[u(t-τ )];
Pour parler franchement, un système fonctionne pendant une période de temps T à partir du moment initial, et les entrées et sorties pendant cette période ont une trajectoire correspondante.
Si l'état de ce système à l'instant T est réexécuté pendant une période de temps T avec l'heure initiale, l'entrée passe de l'heure initiale à la même forme qu'avant, jetez un œil La sortie est-elle la même qu'avant
(Par exemple, en prenant une fusée comme exemple, l'entrée fait référence à l'énergie de la poussée, et la sortie fait référence à l'accélération
La première fusée est lancée dans des conditions normales. Lorsqu'elle fonctionne pendant un temps T, un trois-. la courbe dimensionnelle Q1 peut être tracée en saisissant l'énergie, l'accélération et le temps
La deuxième fusée est lancée dans le même état que la première fois à l'heure T ; fonctionnant pendant un temps T (le changement de l'énergie d'entrée avec le temps est le même que la première fois), à ce moment, l'énergie d'entrée et la sortie d'accélération, et le temps changent pour tracer une autre courbe tridimensionnelle Q2 Les deux courbes Q1 et Q2. ne se chevauchent pas dans l'accélération de sortie (cela changera certainement car la masse au temps T devient plus petite))
est égale à la valeur y(t-τ) obtenue en premier effectuer une transformation de système H[ ▪] sur le signal d'entrée u(t), puis effectuer un décalage temporel, c'est-à-dire H[u(t-τ) )]=y(t-τ).
Par exemple :
1. Déterminez si le système y(t)=cos[u(t)],t>0 est un système invariant dans le temps :
1. , procédez d'abord. Le décalage temporel est u(t-τ), puis la valeur obtenue par transformation du système est cos[u(t-τ)], t>0
2; effectuez d'abord la transformation du système comme cos[u(t)], puis la valeur obtenue par décalage temporel est cos[u(t-τ)], t>0
sont égaux, donc le système est invariant dans le temps ; système.
2. Déterminez si le système y(t)=u(t)§cost est un système invariant dans le temps :
1 Entrez le signal u(t), effectuez d'abord un décalage temporel vers u(t). -τ), La valeur obtenue par transformation du système est u(t-τ)§cost, t>0
2). Signal d'entrée u(t), effectuez d'abord la transformation du système en u(t)§cost, et puis effectuez un décalage temporel. La valeur obtenue est u(t-τ) ▪cos(t-τ), t>0;
u(t-τ) ▪cost≠u(t-τ) ▪cos(t-τ ), donc le système est un système variable dans le temps
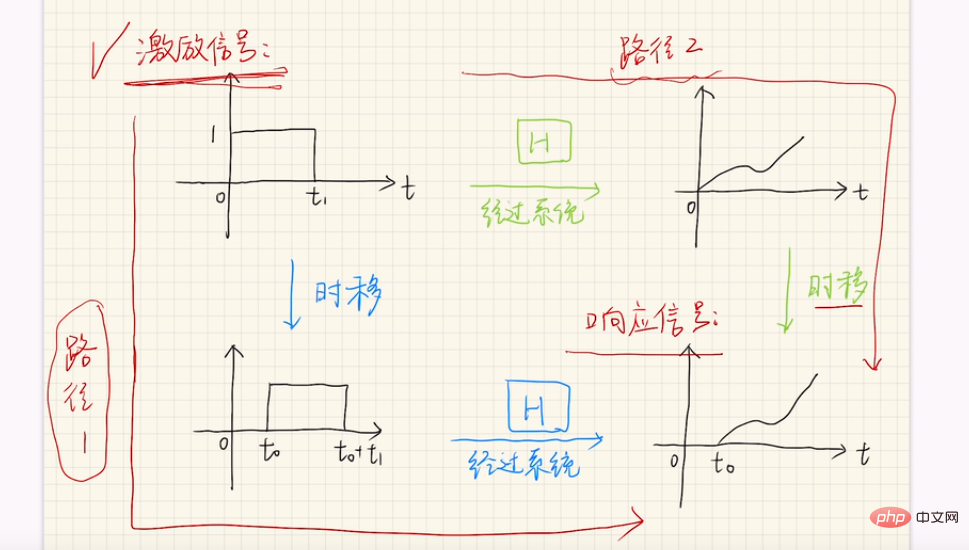
Ce que nous examinons en fin de compte, c'est si les images finales de les deux chemins (c'est-à-dire l'image dans le coin inférieur droit) se chevauchent
Remarque : La méthode d'analyse ci-dessus peut également être utilisée pour tester s'il s'agit d'un système stable en utilisant la méthode que j'ai mentionnée. , c'est-à-dire : en supposant que u est entré en t1, la sortie est y et u est entré en t2, et la sortie est Assurez-vous simplement que la valeur est toujours y
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Interprétation des autorisations de fichiers sous système Linux - (utilisateur, groupe, lecture, écriture et exécution)
- Autorisations par défaut des fichiers sous le système Linux et rôle des attributs cachés
- Une exploration préliminaire du système de points enterrés
- 【Linux】 Netdata 1.25.0 est disponible ! Système de surveillance des performances et de la santé en temps réel
- Nouvelles fonctionnalités et modifications dans le système de file d'attente Laravel 8
- Quelles sont les caractéristiques du système d'exploitation Windows ?
- Explication détaillée de la façon de définir les variables système en php
- De quoi est constitué un système CNC ?

