Un certain arbre binaire a 5 nœuds de degré 2. Quel est le nombre de nœuds feuilles de cet arbre binaire ?

En informatique, un arbre binaire est une structure arborescente comportant au plus deux sous-arbres par nœud. Habituellement, les sous-arbres sont appelés « sous-arbre gauche » et « sous-arbre droit ». Les arbres binaires sont souvent utilisés pour implémenter des arbres de recherche binaires et des tas binaires.

Un arbre binaire avec une profondeur k et 2 ^ k-1 nœuds est appelé un arbre binaire complet. La caractéristique de ce type d’arbre est que le nombre de nœuds à chaque niveau correspond au nombre maximum de nœuds. Dans un arbre binaire, à l'exception du dernier niveau, si tous les autres niveaux sont pleins, et que soit le dernier niveau est plein, soit qu'il manque plusieurs nœuds consécutifs à droite, alors l'arbre binaire est un arbre binaire complet. La profondeur d'un arbre binaire complet avec n nœuds est floor(log2n)+1. Un arbre binaire complet de profondeur k a au moins 2k-1 nœuds feuilles et au plus 2k-1 nœuds.

Un certain arbre binaire a 5 nœuds de degré 2. Quel est le nombre de nœuds feuilles de cet arbre binaire ?

La relation entre le nombre de nœuds feuilles dans un arbre binaire et le nombre de nœuds de degré 2 est : le nombre de nœuds de degré 2 = le nombre de nœuds feuilles - 1 ;

Donc, le nombre de nœuds feuilles = Le nombre de nœuds de degré 2+1=6.

Expansion :

L'arbre binaire est défini de manière récursive et ses nœuds sont divisés en sous-arbres gauche et droit. Logiquement, les arbres binaires ont cinq formes de base :

<.>

Arbre binaire vide - comme indiqué en (a) ;
Un arbre binaire avec un seul nœud racine - comme indiqué en (b) ;

2. Uniquement le sous-arbre de gauche - comme indiqué en (c)

3. Uniquement le sous-arbre de droite - comme indiqué en (d) ; >
4. Arbre binaire complet - Figure (e).

Remarque : Bien que les arbres binaires présentent de nombreuses similitudes avec les arbres, les arbres binaires ne sont pas un cas particulier d'arbres.

Type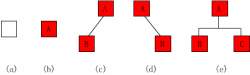

(1) Arbre binaire complet - Si la hauteur de l'arbre binaire est h, à l'exception de la h-ème couche, le nombre de nœuds dans toutes les autres couches (1~h -1) atteint le maximum Il y a des nœuds feuilles dans la h-ième couche, et les nœuds feuilles sont disposés de gauche à droite. Il s'agit d'un arbre binaire complet.

(2) Arbre binaire complet - un arbre binaire dans lequel chaque nœud, à l'exception des nœuds feuilles, a des sous-feuilles gauche et droite, et les nœuds feuilles sont tous en bas.

(3) Arbre binaire équilibré - Un arbre binaire équilibré est également appelé arbre AVL (différent de l'algorithme AVL). C'est un arbre de tri binaire et possède les propriétés suivantes : c'est un arbre vide ou il). La valeur absolue de la différence de hauteur entre les sous-arbres gauche et droit ne dépasse pas 1, et les sous-arbres gauche et droit sont tous deux des arbres binaires équilibrés.

Pour plus de connaissances connexes, veuillez faire attention au

Site Web PHP chinois

 ! !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!