Maison >Problème commun >Algorithme de traversée d'arbre binaire
Algorithme de traversée d'arbre binaire
- 步履不停original
- 2019-06-20 11:51:0722509parcourir

A. Traversée d'arbre binaire
1. Parcours de précommande de l'arbre binaire :
(1) Si l'arbre binaire est vide, c'est une non-opération et ne renvoie rien.
(2) Visitez le nœud racine.
(3) Traversée de précommande du sous-arbre gauche.
(4) La précommande traverse le sous-arbre droit.
a. Algorithme récursif pour le parcours pré-commandé d'arbres binaires :
void PreOrderTraverse(BiTree BT)
{ if(BT)
{
printf("%c",BT->data); //访问根结点
PreOrderTraverse(BT->lchild); //前序遍历左子树
PreOrderTraverse(BT->rchild); //前序遍历右子树 }
} b. Algorithme non récursif pour la traversée de pré-ordre d'arbre binaire en utilisant la pile pour stocker le sous-arbre droit de chaque nœud :
( 1) Lorsque l'arborescence est vide, pointez le pointeur p vers le nœud racine, et p est le pointeur de nœud actuel.
(2) Visitez d'abord le nœud actuel p et poussez p dans la pile S.
(3) Laissez p pointer vers son enfant gauche.
(4) Répétez les étapes (2) et (3) jusqu'à ce que p soit vide.
(5) Extrayez l'élément supérieur de la pile S et pointez p vers l'enfant droit de cet élément.
(6) Répétez les étapes (2) ~ (5) jusqu'à ce que p soit vide et que la pile S soit également vide.
(7) Fin du parcours.
Algorithme non récursif utilisant le parcours pré-commandé de la pile :
void PreOrderNoRec(BiTree BT)
{
stack S;
BiTree p=BT->root; while((NULL!=p)||!StackEmpty(S))
{ if(NULL!=p)
{
printf("%c",p->data);
Push(S,p);
p=p->lchild;
} else
{
p=Top(S);
Pop(S);
p=p->rchild;
}
}
}c. stockage Algorithme non récursif pour le parcours pré-commandé d'un arbre binaire :
void PreOrder(pBinTreeNode pbnode)
{
pBinTreeNode stack[100];
pBinTreeNode p; int top;
top=0;
p=pbnode; do
{ while(p!=NULL)
{
printf("%d\n",p->data); //访问结点p
top=top+1;
stack[top]=p;
p=p->llink; //继续搜索结点p的左子树 } if(top!=0)
{
p=stack[top];
top=top-1;
p=p->rlink; //继续搜索结点p的右子树 }
}while((top!=0)||(p!=NULL));
}2. Parcours dans l'ordre d'un arbre binaire :
( 1) Si l'arborescence binaire est vide, c'est une opération sans opération et ne renvoie rien.(2) Parcours dans l'ordre du sous-arbre gauche.
(3) Visitez le nœud racine.
(4) Parcours dans l'ordre du sous-arbre droit.
void InOrderTraverse(BiTree BT)
{ if(BT)
{
InOrderTraverse(BT->lchild); //中序遍历左子树
printf("%c",BT->data); //访问根结点
InOrderTraverse(BT->rchild); //中序遍历右子树 }
} b. Algorithme non récursif pour la traversée dans l'ordre des arbres binaires à l'aide du stockage sur pile :
(2) Poussez p dans la pile S et faites pointer p vers son enfant gauche.
(3) Répétez l'étape (2) jusqu'à ce que p soit vide.
(4) Extrayez l'élément supérieur de la pile S et pointez p vers cet élément.
(5) Visitez le nœud actuel p et pointez p vers son enfant droit.
(6) Répétez les étapes (2) ~ (5) jusqu'à ce que p soit vide et que la pile S soit également vide.
(7) La traversée se termine.
Algorithme non récursif utilisant le parcours dans l'ordre de la pile :
void IneOrderNoRec(BiTree BT)
{
stack S;
BiTree p=BT->root; while((NULL!=p)||!StackEmpty(S))
{ if(NULL!=p)
{
Push(S,p);
p=p->lchild;
} else
{
p=Top(S);
Pop(S);
printf("%c",p->data);
p=p->rchild;
}
}
}c. fork binaire Algorithme non récursif pour le parcours dans l'ordre d'un arbre binaire stocké dans une liste chaînée :
void InOrder(pBinTreeNode pbnode)
{
pBinTreeNode stack[100];
pBinTreeNode p; int top;
top=0;
p=pbnode; do
{ while(p!=NULL)
{
top=top+1;
stack[top]=p; //结点p进栈
p=p->llink; //继续搜索结点p的左子树 } if(top!=0)
{
p=stack[top]; //结点p出栈
top=top-1;
printf("%d\n",p->data); //访问结点p
p=p->rlink; //继续搜索结点p的右子树 }
}while((top!=0)||(p!=NULL));
}3. un arbre binaire :
(2) Parcours post-ordre du sous-arbre gauche.
(3) Traversée post-ordre du sous-arbre droit.
(4) Visitez le nœud racine.
void PostOrderTraverse(BiTree BT)
{ if(BT)
{
PostOrderTraverse(BT->lchild); //后序遍历左子树
PostOrderTraverse(BT->rchild); //后序遍历右子树
printf("%c",BT->data); //访问根结点 }
}b.使用栈存储的二叉树后序遍历的非递归算法:
算法思想:首先扫描根结点的所有左结点并入栈,然后出栈一个结点,扫描该结点的右结点并入栈,再扫描该右结点的所有左结点并入栈,当一个结点的左、右子树均被访问后再访问该结点。因为在递归算法中,左子树和右子树都进行了返回,因此为了区分这两种情况,还需要设置一个标识栈tag,当tag的栈顶元素为0时表示从左子树返回,为1表示从右子树返回。
(1)当树为空时,将指针p指向根结点,p为当前结点指针。
(2)将p压入栈S中,0压入栈tag中,并令p指向其左孩子。
(3)重复执行步骤(2),直到p为空。
(4)如果tag栈中的栈顶元素为1,跳至步骤(6)。
(5)如果tag栈中的栈顶元素为0,跳至步骤(7)。
(6)将栈S的栈顶元素弹出,并访问此结点,跳至步骤(8)。
(7)将p指向栈S的栈顶元素的右孩子。
(8)重复执行步骤(2)~(7),直到p为空并且栈S也为空。
(9)遍历结束。
使用栈的后序遍历非递归算法:
void PostOrderNoRec(BiTree BT)
{
stack S;
stack tag;
BiTree p=BT->root; while((NULL!=p)||!StackEmpty(S))
{ while(NULL!=p)
{
Push(S,p);
Push(tag,0);
p=p->lchild;
} if(!StackEmpty(S))
{ if(Pop(tag)==1)
{
p=Top(S);
Pop(S);
printf("%c",p->data);
Pop(tag); //栈tag要与栈S同步 } else
{
p=Top(S); if(!StackEmpty(S))
{
p=p->rchild;
Pop(tag);
Push(tag,1);
}
}
}
}
}c.使用二叉链表存储的二叉树后序遍历非递归算法:
void PosOrder(pBinTreeNode pbnode)
{
pBinTreeNode stack[100]; //结点的指针栈 int count[100]; //记录结点进栈次数的数组 pBinTreeNode p; int top;
top=0;
p=pbnode; do
{ while(p!=NULL)
{
top=top+1;
stack[top]=p; //结点p首次进栈
count[top]=0;
p=p->llink; //继续搜索结点p的左子树 }
p=stack[top]; //结点p出栈
top=top-1; if(count[top+1]==0)
{
top=top+1;
stack[top]=p; //结点p首次进栈
count[top]=1;
p=p->rlink; //继续搜索结点p的右子树 } else
{
printf("%d\n",p->data); //访问结点p
p=NULL;
}
}while((top>0));
}B 线索化二叉树:

typedef struct node
{
DataType data; struct node *lchild, *rchild; //左、右孩子指针 int ltag, rtag; //左、右线索
}TBinTNode; //结点类型
typedef TBinTNode *TBinTree;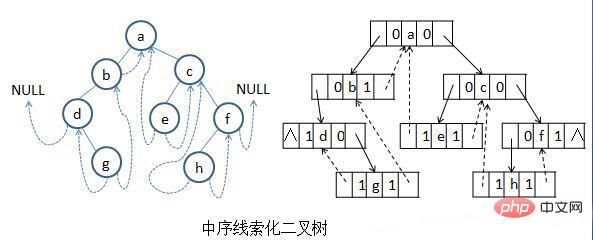
(1)中序线索化二叉树的算法:
void InOrderThreading(TBinTree p)
{ if(p)
{
InOrderThreading(p->lchild); //左子树线索化 if(p->lchild)
p->ltag=0; else
p->ltag=1; if(p->rchild)
p->rtag=0; else
p->rtag=1; if(*(pre)) //若*p的前驱*pre存在 { if(pre->rtag==1)
pre->rchild=p; if(p->ltag==1)
p->lchild=pre;
}
pre=p; //另pre是下一访问结点的中序前驱
InOrderThreading(p->rchild); //右子树线索化 }
}(2)在中序线索化二叉树下,结点p的后继结点有以下两种情况:
①结点p的右子树为空,那么p的右孩子指针域为右线索,直接指向结点p的后继结点。②结点p的右子树不为空,那么根据中序遍历算法,p的后继必是其右子树中第1个遍历到的结点。
TBinTNode *InOrderSuc(BiThrTree p)
{
TBinTNode *q; if(p->rtag==1) //第①情况 return p->rchild; else //第②情况 {
q=p->rchild; while(q->ltag==0)
q=q->lchild; return q;
}
}中序线索化二叉树求前驱结点的算法:
TBinTNode *InOrderPre(BiThrTree p)
{
TBinTNode *q; if(p->ltag==1) return p->lchild; else
{
q=p->lchild; //从*p的左孩子开始查找 while(q->rtag==0)
q=q->rchild; return q;
}
}(3)遍历中序线索化二叉树的算法
void TraversInOrderThrTree(BiThrTree p)
{ if(p)
{ while(p->ltag==0)
p=p->lchild; while(p)
{
printf("%c",p->data);
p=InOrderSuc(p);
}
}
}Pour des articles plus techniques liés aux questions fréquemment posées, veuillez visiter la colonne FAQ pour apprendre !
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

