Propriétés de base des arbres binaires

En informatique, un arbre binaire est une structure arborescente comportant au plus deux sous-arbres par nœud. Habituellement, les sous-arbres sont appelés « sous-arbre gauche » et « sous-arbre droit ». Les arbres binaires sont souvent utilisés pour implémenter des arbres de recherche binaires et des tas binaires.

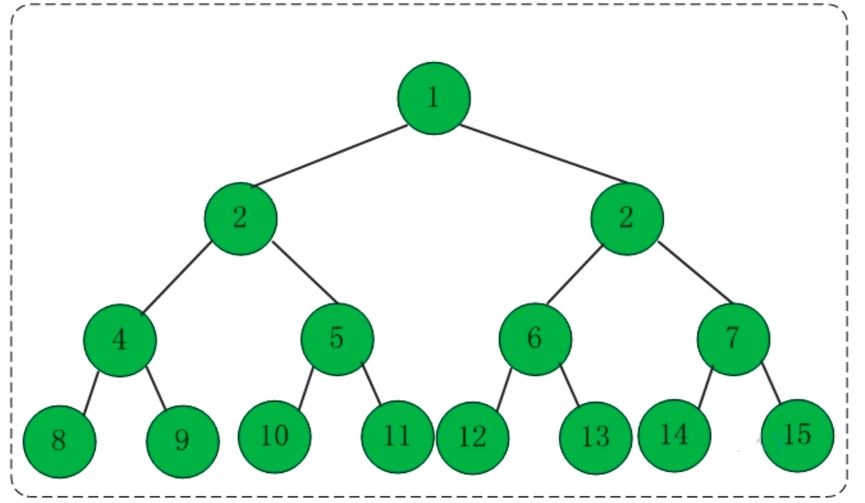
Un arbre binaire avec une profondeur k et 2 ^ k-1 nœuds est appelé un arbre binaire complet. La caractéristique de ce type d’arbre est que le nombre de nœuds à chaque niveau correspond au nombre maximum de nœuds. Dans un arbre binaire, à l'exception du dernier niveau, si tous les autres niveaux sont pleins et que le dernier niveau est soit plein, soit dépourvu de plusieurs nœuds consécutifs à droite, alors l'arbre binaire est un arbre binaire complet. La profondeur d'un arbre binaire complet avec n nœuds est floor(log2n)+1. Un arbre binaire complet de profondeur k a au moins 2k-1 nœuds feuilles et au plus 2k-1 nœuds.

Propriétés de l'arbre binaire

(1) Dans un arbre binaire non vide, le nombre total de nœuds dans le i-ème niveau ne dépasse pas 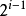, i>=1;

(2) Un arbre binaire de profondeur h a au plus 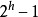nœuds (h>=1) et au moins h nœuds

(3) Pour tout arbre binaire, si le nombre de nœuds feuilles est N0 et le nombre total de nœuds de degré 2 est N2, alors N0=N2+1

(4) La profondeur d'un arbre binaire complet avec n ; nodes est 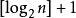(Remarque : [ ] signifie arrondi à l'inférieur)

Cours recommandé : Tutoriel PHP.

(5) Si chaque nœud d'un arbre binaire complet à N nœuds est stocké de manière séquentielle, les nœuds ont la relation suivante :

Si I est le numéro de nœud, alors si I> ;1, alors le numéro de son nœud parent est I/2

Si 2*I<=N, alors le numéro de son enfant gauche (c'est-à-dire le nœud racine du sous-arbre gauche) est 2. *I ; Si 2*I>N, alors il n'y a plus d'enfant gauche

Si 2*I+1<=N, alors le numéro de nœud de son enfant droit est 2*I+1 ; *I+1> N, alors il n’y a pas de bon enfant.

(6) Étant donné N nœuds, h(N) arbres binaires différents peuvent être formés.

h(N) est le Nième terme du nombre de Cattelan. h(n)=C(2*n,n)/(n+1).

(7) Il y a i points de branchement, I est la somme des longueurs de route de tous les points de branchement, J est la somme des longueurs de route des feuilles J=I+2i [2]

Concepts de base

L'arbre binaire est défini de manière récursive et ses nœuds sont divisés en sous-arbres gauche et droit Logiquement, les arbres binaires ont cinq formes de base :

( 1) Arbre binaire vide - comme la figure (a) ;

(2) Un arbre binaire avec un seul nœud racine - comme indiqué dans (b)

(3) Un seul nœud gauche ; sous-arbre - comme indiqué dans (c);

(4) Uniquement le sous-arbre de droite - comme indiqué dans la figure (d)

(5) Arbre binaire complet - comme indiqué dans (e) ; .

Remarque : Bien que les arbres binaires présentent de nombreuses similitudes avec les arbres, les arbres binaires ne sont pas un cas particulier d'arbres. [1]

Type

(1) Arbre binaire complet - si la hauteur de l'arbre binaire est h, à l'exception du h-ème niveau, tous les autres niveaux (1~h -1) Le nombre de nœuds a atteint le nombre maximum. Il y a des nœuds feuilles dans la couche h, et les nœuds feuilles sont disposés de gauche à droite.

(2) Arbre binaire complet - un arbre binaire dans lequel chaque nœud, à l'exception des nœuds feuilles, a des sous-feuilles gauche et droite, et les nœuds feuilles sont tous en bas.

(3) Arbre binaire équilibré - Un arbre binaire équilibré est également appelé arbre AVL (différent de l'algorithme AVL). C'est un arbre de tri binaire et possède les propriétés suivantes : c'est un arbre vide ou il). La valeur absolue de la différence de hauteur entre les sous-arbres gauche et droit ne dépasse pas 1, et les sous-arbres gauche et droit sont tous deux des arbres binaires équilibrés.

Discrimination

L'arbre binaire n'est pas un cas particulier d'arbre Bien qu'il présente de nombreuses similitudes avec l'arbre, il existe deux différences principales entre l'arbre et l'arbre binaire :

1. Il n'y a pas de limite au degré maximum d'un nœud dans un arbre, alors que le degré maximum d'un nœud d'arbre binaire est de 2

2. nœuds d'un arbre, tandis que les nœuds d'un arbre binaire Il y a à gauche et à droite.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!