Introduction aux arbres binaires (tas binaires) en JavaScript (exemples de code)

Cet article vous apporte une introduction (exemple de code) sur les arbres binaires (tas binaires) en JavaScript. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

Arbre binaire

L'arbre binaire est une structure arborescente. Il se caractérise par le fait que chaque nœud a au plus deux nœuds de branche. Un arbre binaire se compose généralement de. nœud racine, nœud de branche et nœud feuille. Chaque nœud de branche est souvent appelé sous-arbre.

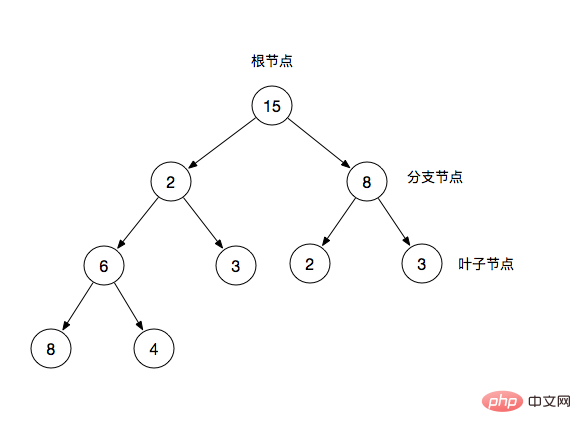
• Nœud racine : le nœud supérieur de l'arbre binaire

• Branche node : En plus du nœud racine et ayant des nœuds feuilles

• nœud feuille : à part lui-même, il n'y a pas d'autres nœuds enfants

Termes courants

Dans un arbre binaire, nous utilisons souvent des nœuds parents et des nœuds enfants pour le décrire. Par exemple, 2 dans l'image est le nœud parent de 6 et 3, et inversement. 6 et 3 sont 2 nœuds enfants

Trois propriétés des arbres binaires

1. Au i-ème niveau de l'arbre binaire, il y a au la plupart des nœuds 2^i-1

• Quand i=1, il n'y a qu'un seul nœud racine, 2^(i-1) = 2^0 = 1

L'arbre binaire de profondeur k est au plus Il y a 2^k-1 nœuds

• Quand i=2, 2 ^k-1 = 2^2 - 1 = 3 nœuds

Pour tout arbre binaire T, si le nombre de points récapitulatifs est n0 et le nombre de nœuds de degré 2 (le nombre de sous-arbres est 2) est n2, alors n0=n2+1

Trois différences principales entre les arbres et les arbres binaires

• Le nombre de nœuds d'un arbre est d'au moins 1, tandis que le nombre de nœuds d'un arbre binaire peut être 0

• Le degré maximum (nombre de nœuds) d'un nœud dans un arbre n'est pas limité, alors que le degré maximum d'un nœud dans un arbre binaire est de 2. Les nœuds sont divisés en nœuds gauche et droit

• Classification des arbres binaires

Les arbres binaires sont divisés en complets arbres binaires et arbres binaires complets

Arbre binaire complet : un arbre binaire de profondeur k et 2 ^ k - 1 nœuds est appelé un arbre binaire complet

• Arbre binaire complet : un arbre binaire complet fait référence au dernier niveau. Un arbre binaire dans lequel le côté gauche est plein, le côté droit peut être plein ou non, et les niveaux restants sont pleins est appelé un arbre binaire complet (un l'arbre binaire complet est également un arbre binaire complet)

Représentation matricielle de l'arbre binaire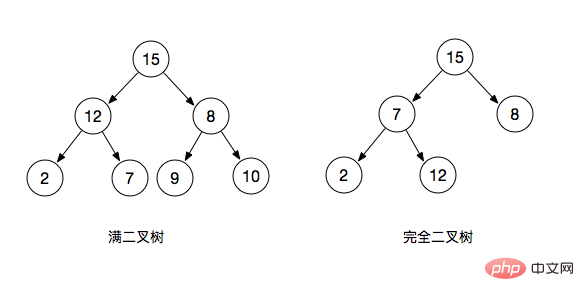Utilisez un tableau pour représenter la structure de l'arbre binaire. Remplissez un ensemble de tableaux en commençant par le nœud racine de haut en bas et de gauche à droite, comme indiqué dans la figure ci-dessous

<.>

Grâce à la figure ci-dessus, nous pouvons analyser que l'arbre binaire complet représenté par le tableau a les propriétés suivantes :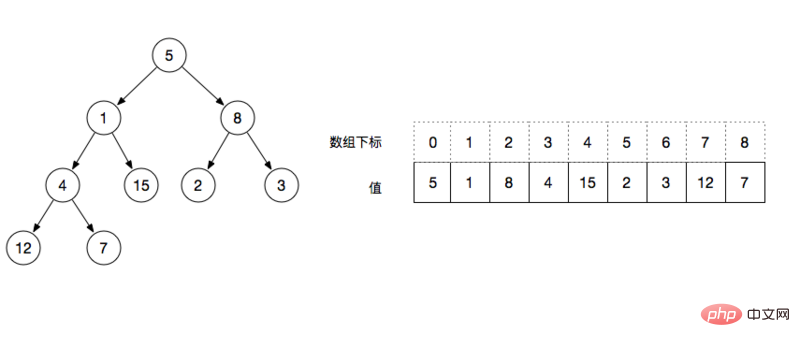

left = index * 2 + 1, par exemple : l'indice du nœud racine est 0, alors la valeur du nœud gauche est l'indice tableau[0＊2+1]=1

• droite = index * 2 + 2, par exemple : l'indice du nœud racine est 0, alors la valeur du nœud droit est l'indice tableau[0＊2+2]=2

• Ordinal>= floor(N/2) sont tous des nœuds feuilles, par exemple : floor(9/2) = 4, alors les valeurs à partir de l'indice 4 sont des nœuds feuilles

• Tas binaire
  La structure d'un tas binaire est représentée par un arbre binaire complet, qui est représenté par un tableau, mais un tas binaire doit satisfaire les propriétés suivantes :

La valeur clé du nœud parent d'un tas binaire est toujours supérieure ou égale à (inférieure ou égale à) la valeur clé de tout nœud enfant

• Lorsque la clé du nœud parent Lorsque la valeur est supérieure ou égale à (inférieure ou égale) à la valeur clé de chacun de ses nœuds enfants, on l'appelle

  max tas (min tas)

• 

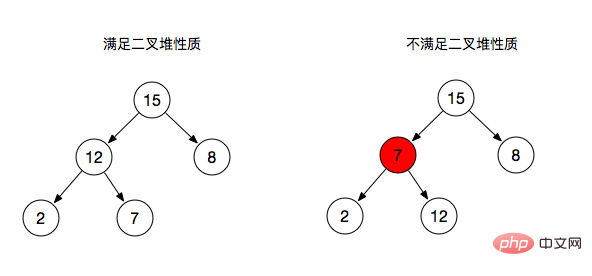
  Comme on peut le voir sur la photo ci-dessus :

Image de gauche : Le nœud parent est toujours supérieur ou égal à son nœud enfant, il satisfait donc aux propriétés d'un tas binaire,

• Image de droite : Nœud de branche 7 , en tant que nœud parent de 2 et 12, ne satisfait pas ses propriétés (supérieures ou égales à son nœud enfant).

• Opérations principales du tas binaire

insérer : insérer un nœud

• supprimer : supprimer un nœud

• max-hepify : Ajuster les propriétés du tas du nœud de branche

• rebuildHeap : Reconstruire l'intégralité du tas binaire

• sort : Trier

• Initialiser un tas binaire
  D'après la brève introduction ci-dessus, nous pouvons savoir que l'initialisation d'un tas binaire est très simple. C'est juste un tableau.

Initialisation d'une structure de tableau

Enregistrer la longueur du tableau

    class Heap{
        constructor(arr){
            this.data = [...arr];
            this.size = this.data.length;
        }
    }

opération de tas maximale max-heapify

max-heapify consiste à mettre chaque élément qui le fait ne satisfait pas le tas maximum. Opération permettant d'ajuster les propriétés d'un nœud de branche.

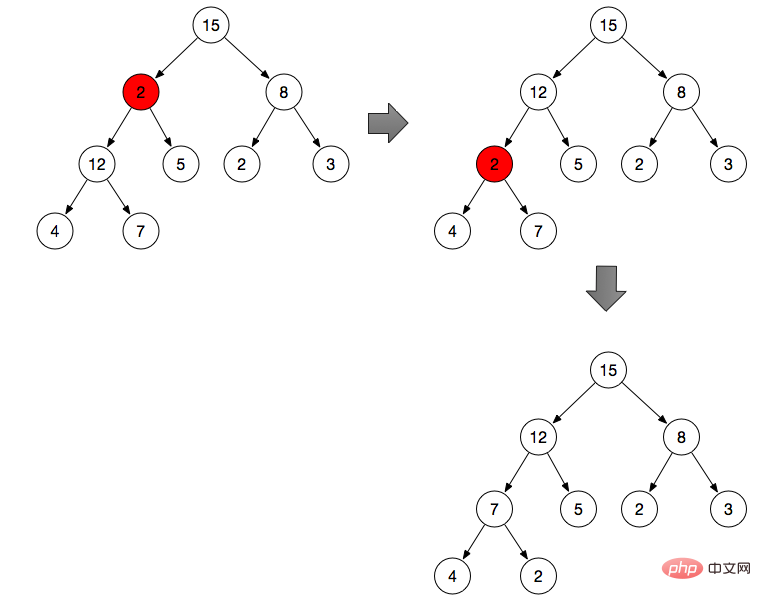
Comme indiqué ci-dessus :

1. Ajustez le nœud de branche 2 (le nœud de branche 2 ne répond pas aux propriétés du tas maximum)

• Par défaut, le nœud de branche est la valeur maximale

Comparez 2 avec la gauche et les branches droites, à partir de 2, 12, Trouvez la valeur maximale dans 5, puis échangez la position avec 2

• Selon les propriétés du tas binaire mentionnées ci-dessus, obtenez la gauche le nœud et le nœud droit du nœud de branche 2 respectivement

• Comparez trois nœuds et obtenez l'indice maximum de la valeur maximale

• Si le nœud lui-même est la valeur maximale, arrêter l'opération

• Échanger le nœud max avec le nœud parent

Répéter l'opération de l'étape 2, trouver la valeur maximale de 2, 4 et 7 et échangez-la avec 2

• Récursif

    maxHeapify(i) {
        let max = i;
        
        if(i >= this.size){
            return;
        }
        // 当前序号的左节点
        const l = i * 2 + 1;
        // 当前需要的右节点
        const r = i * 2 + 2;
        
        // 求当前节点与其左右节点三者中的最大值
        if(l  this.data[max]){
            max = l;
        }
        if(r  this.data[max]){
            max = r;
        }
        
        // 最终max节点是其本身,则已经满足最大堆性质，停止操作
        if(max === i) {
            return;
        }
        
        // 父节点与最大值节点做交换
        const t = this.data[i];
        this.data[i] = this.data[max];
        this.data[max] = t;
        
        // 递归向下继续执行
        return this.maxHeapify(max);
    }

Reconstruit Tas

Nous pouvons voir que le tas juste initialisé est représenté par un tableau. À ce stade, il se peut qu'il ne satisfasse pas les propriétés d'un tas maximum ou d'un tas minimum. À ce stade, nous devrons peut-être construire le tas. tout un tas dans ce que nous voulons.
Nous avons effectué l'opération max-heapify ci-dessus, et max-heapify n'ajuste qu'un certain nœud de branche. Pour construire le tas entier en un tas maximum, vous devez effectuer une opération max-heapify sur tous les nœuds de branche. Dans la figure ci-dessous, nous devons effectuer des opérations max-hepify sur les quatre nœuds de branche 12, 3, 2 et 15 en séquence

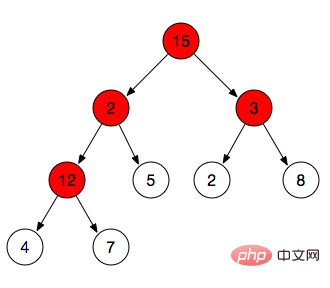
Étapes spécifiques :

• Trouver tous les nœuds de branche : Les propriétés du tas mentionnées ci-dessus mentionnent que le numéro de série du nœud feuille>=Math.floor(n/2), il est donc plus petit que le numéro de série de Math.floor(n/2) Ce sont tous des nœuds que nous devons ajuster.

• Par exemple, le tableau affiché au milieu est [15,2,3,12,5,2,8,4,7] => (9/2 )=4 => Ceux dont l'indice est inférieur à 4 sont 15, 2, 3 et 12 (nœuds qui doivent être ajustés), tandis que 5, 2, 8, 4 et 7 sont des nœuds feuilles.

• Effectuer l'opération maxHeapify sur tous les nœuds trouvés

    rebuildHeap(){
        // 叶子节点
        const L = Math.floor(this.size / 2);
        for(let i = L - 1; i>=0; i--){
            this,maxHeapify(i);
        }
    }

Tri maximal du tas

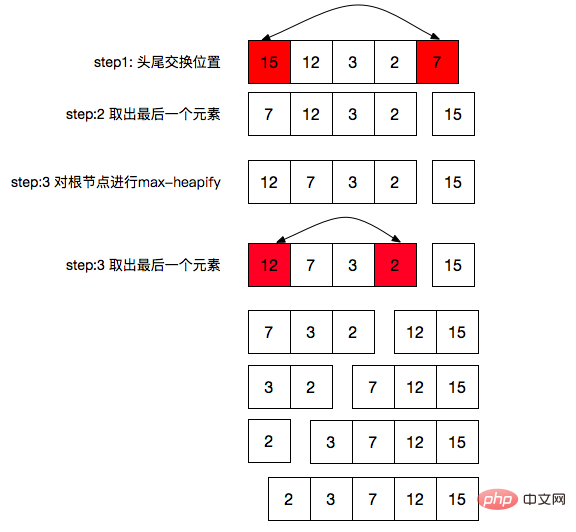
Tri maximal des tas, comme indiqué dans la figure ci-dessus :

• Échanger les positions de tête et de queue

• Le dernier élément est retiré du tas, ce qui équivaut à la taille 1 du tas

• , puis une opération max-heapify est effectuée sur le nœud racine du tas

• Répétez les trois étapes ci-dessus jusqu'à ce que size=0 (nous avons déjà effectué cette condition aux limites dans la fonction max-heapify)

    sort() {
        for(let i = this.size - 1; i > 0; i--){
            swap(this.data, 0, i);
            this.size--;
            this.maxHeapify(0);
        }
    }

Insertion et suppression

L'insertion et la suppression de ceci est relativement simple, qui consiste à insérer et supprimer un tableau

• insérer jusqu'à la fin

• longueur du tas +1

• Déterminer s'il s'agit toujours d'un tas maximum après l'insertion

• Sinon, reconstruire le tas

  insert(key) {
    this.data[this.size] = key;
    this.size++
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

• Supprimer un élément du tableau

• Longueur du tas -1

• Déterminez s'il s'agit d'un tas

• Sinon, refactorisez le tas

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

Code complet

/**
 * 最大堆
 */

function left(i) {
  return i * 2 + 1;
}

function right(i) {
  return i * 2 + 2;
}

function swap(A, i, j) {
  const t = A[i];
  A[i] = A[j];
  A[j] = t;
}

class Heap {
  constructor(arr) {
    this.data = [...arr];
    this.size = this.data.length;
  }

  /**
   * 重构堆
   */
  rebuildHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i--) {
      this.maxHeapify(i);
    }
  }

  isHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i++) {
      const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
      const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;

      const max = Math.max(this.data[i], l, r);

      if (max !== this.data[i]) {
        return false;
      }
      return true;
    }
  }

  sort() {
    for (let i = this.size - 1; i > 0; i--) {
      swap(this.data, 0, i);
      this.size--;
      this.maxHeapify(0);
    }
  }

  insert(key) {
    this.data[this.size++] = key;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  /**
   * 堆的其他地方都满足性质
   * 唯独跟节点，重构堆性质
   * @param {*} i
   */
  maxHeapify(i) {
    let max = i;

    if (i >= this.size) {
      return;
    }

    // 求左右节点中较大的序号
    const l = left(i);
    const r = right(i);
    if (l  this.data[max]) {
      max = l;
    }

    if (r  this.data[max]) {
      max = r;
    }

    // 如果当前节点最大，已经是最大堆
    if (max === i) {
      return;
    }

    swap(this.data, i, max);

    // 递归向下继续执行
    return this.maxHeapify(max);
  }
}

module.exports = Heap;

Résumé

La discussion sur le tas se termine ici. Le tas est relativement simple dans un arbre binaire et est souvent utilisé pour le tri et les files d'attente prioritaires. Le cœur du tas est l’opération max-heapify et les trois propriétés du tas.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!