Un ensemble de diagrammes de structures de données pour vous aider à comprendre la complexité temporelle

Cet article utilise un ensemble d'images pour vous permettre de comprendre facilement ce qu'est la complexité temporelle. Il est intéressant et vivant, et a une certaine valeur d'apprentissage. Les amis intéressés peuvent venir le découvrir. .

La signification de la complexité temporelle

Qu'est-ce que la complexité temporelle exactement ? Imaginons une scène : un jour, Xiao Hui et Da Huang ont rejoint une entreprise en même temps...

Un jour plus tard, Xiao Hui et Da Huang ont chacun livré leur code de marchandises, les fonctions mises en œuvre par le code aux deux extrémités sont similaires. Le code de Dahuang prend 100 millisecondes pour s'exécuter une fois et occupe 5 Mo de mémoire. Le code de Xiao Hui prend 100 secondes pour s'exécuter une fois et occupe 500 Mo de mémoire. Alors...

On constate que mesurer la qualité du code comprend deux indicateurs très importants :

1. Durée d'exécution;

2. Espace occupé.

Opérations de base Nombre d'exécutions

Concernant le nombre d'exécutions des opérations de base du code, nous utilisons quatre scènes de la vie comme analogie :

Scénario 1 :Donnez à Xiao Hui une miche de pain de 10 pouces. Xiao Hui en mange 1 pouce tous les 3 jours. Combien de jours faut-il pour manger la miche entière ?

La réponse est naturellement 3 X 10 = 30 jours.

Et si la longueur du pain est de N pouces ?

Il faudra 3 X n = 3n jours pour manger tout le pain à ce moment là.

Si une fonction est utilisée pour exprimer ce temps relatif, il peut être enregistré sous la forme T(n) = 3n.

Scène 2 : Donnez à Xiao Hui une miche de pain de 16 pouces. Xiao Hui mange la moitié de la longueur restante du pain tous les 5 jours, 8 pouces pour la première fois et 8 pouces. pour la deuxième fois, 4 pouces sont tombés et 2 pouces ont été mangés pour la troisième fois... Alors combien de jours faudra-t-il à Xiao Hui pour manger seulement 1 pouce de pain ?

Pour traduire cette question, le nombre 16 est continuellement divisé par 2. Combien de fois le résultat sera-t-il égal à 1 ? Cela implique des logarithmes en mathématiques. Le logarithme de 16 en base 2 peut être abrégé en log16.

Il faut donc 5 X log16 = 5 X 4 = 20 jours pour manger seulement 1 pouce de pain.

Et si la longueur du pain est de N pouces ?

Cela prend 5 X logn = 5logn jours, enregistré sous la forme T(n) = 5logn.

Scène 3 : Donnez à Xiao Hui un morceau de pain de 10 pouces et un pilon de poulet. Xiao Hui mange un pilon tous les 2 jours. Alors, combien de jours faut-il à Xiao Hui pour manger toute la cuisse de poulet ?

La réponse est naturellement 2 jours. Parce que j'ai seulement dit que je mangeais des cuisses de poulet, ce qui n'a rien à voir avec le pain de 10 pouces.

Et si la longueur du pain est de N pouces ?

Peu importe la durée du pain, le temps nécessaire pour manger les cuisses de poulet est toujours de 2 jours, enregistré comme T(n) = 2.

Scène 4 : Donnez à Xiao Hui une miche de pain de 10 pouces. Il faudra à Xiao Hui 1 jour pour manger le premier pouce, 2 jours pour manger le deuxième pouce et 2 jours pour manger le deuxième pouce. troisième pouce. Il faut 3 jours pour manger un pouce... Chaque pouce supplémentaire prend un jour de plus. Alors combien de jours faut-il à Xiao Hui pour manger tout le pain ?

La réponse est la somme de 1 à 10, soit 55 jours.

Et si la longueur du pain est de N pouces ?

Pour manger le pain entier à ce moment-là, il faut 1+2+3+......+ n-1 + n = (1+n)*n/2 = 0,5n^2 + 0,5n.

Enregistré sous la forme T(n) = 0,5n^2 + 0,5n.

Ce qui précède est le temps relatif passé à manger. Cette idée s'applique également aux statistiques du nombre d'opérations de base du programme. Les quatre scénarios correspondent maintenant aux quatre méthodes d'exécution les plus courantes dans le programme :

Scénario 1 : T(n) = 3n, le nombre d'exécutions est linéaire.

void eat1(int n){
    for(int i=0; i<n; i++){;
        System.out.println("等待一天");
        System.out.println("等待一天");
        System.out.println("吃一寸面包");
    }
}
vo

Scénario 2 : T(n) = 5logn, le nombre d'exécutions est logarithmique.

void eat2(int n){
   for(int i=1; i<n; i*=2){
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("吃一半面包");
   }
}

Scénario 3 : T(n) = 2, le nombre d'exécutions est constant.

void eat3(int n){
   System.out.println("等待一天");
   System.out.println("吃一个鸡腿");
}

Scénario 4 : T(n) = 0,5n^2 + 0,5n, le nombre d'exécutions est un polynôme.

void eat4(int n){
   for(int i=0; i<n; i++){
       for(int j=0; j<i; j++){
           System.out.println("等待一天");
       }
       System.out.println("吃一寸面包");
   }
}

Complexité temporelle asymptotique

Avec la fonction T(n) du nombre de temps d'exécution des opérations de base, peut-on analyser et comparer le temps d'exécution d'un morceau de code ? Certaines difficultés subsistent.

Par exemple, le temps relatif de l'algorithme A est T(n) = 100n, et le temps relatif de l'algorithme B est T(n) = 5n^2. Lequel des deux a une durée d'exécution la plus longue ? Cela dépend de la valeur de n.

Donc, à l'heure actuelle, il existe le concept de complexité temporelle asymptotique (complexité temporelle asymptotique). La définition officielle est la suivante :

S'il existe une fonction f(n), telle. que lorsque n tend vers l'infini. Lorsque , la valeur limite de T(n)/f(n) est une constante non égale à zéro, alors f(n) est dit fonction du même ordre de grandeur que T(n) .

Notée T(n) = O(f(n)), O(f(n)) est appelée la complexité temporelle asymptotique de l'algorithme, ou complexité temporelle en abrégé.

La complexité temporelle asymptotique est représentée par un O majuscule, c'est pourquoi elle est également appelée notation Big O.

Comment dériver la complexité temporelle ? Il existe les principes suivants :

1. Si le temps d'exécution est de grandeur constante, utilisez une constante 1 pour le représenter

2. ; Ne conserver dans la fonction temporelle que le terme d'ordre le plus élevé

3. Si le terme d'ordre le plus élevé existe, le coefficient devant le terme d'ordre le plus élevé est omis.

Retournons maintenant sur les quatre scènes.

Scénario 1 :

T(n) = 3n

Le terme d'ordre le plus élevé est 3n, en omettant le coefficient 3 et la conversion temps La complexité est :

T(n) = O(n)

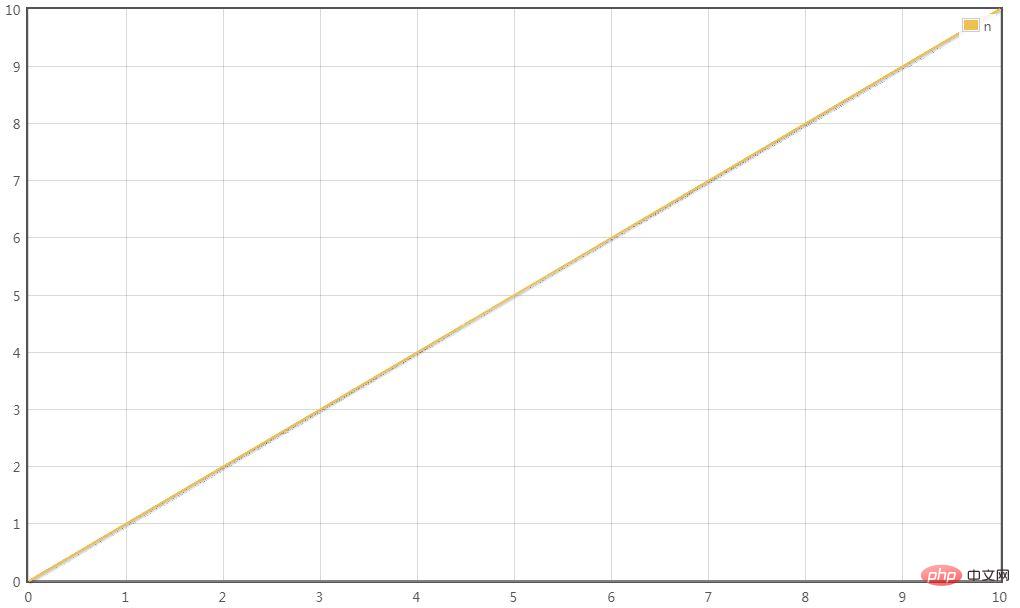
Scénario 2 :

T (n) = 5logn

Le terme d'ordre le plus élevé est 5logn, en omettant le coefficient 5, et la complexité temporelle de la transformation est :

T (n) = O (logn)

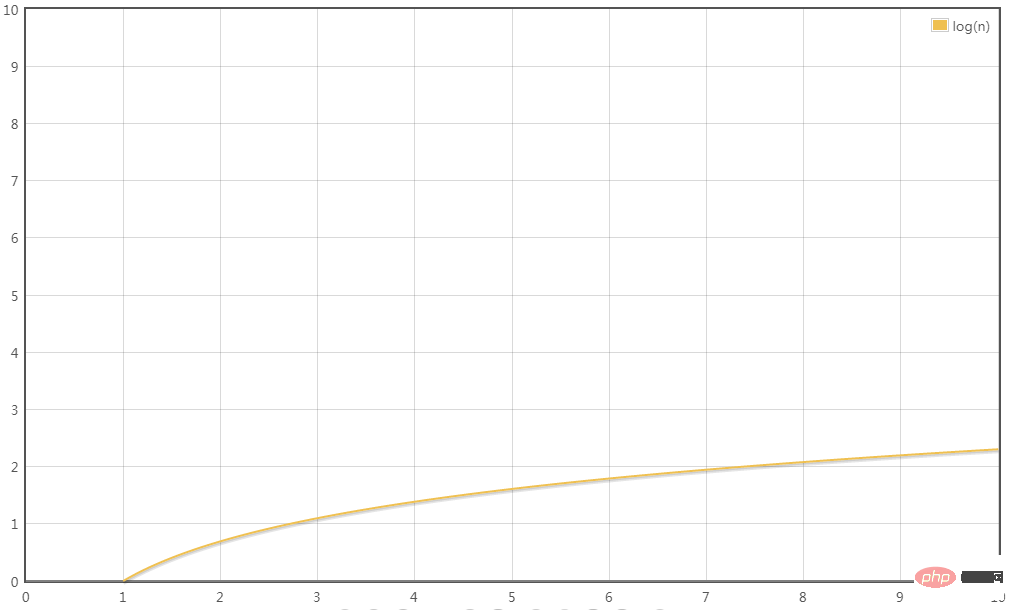
Scénario 3 :

T(n) = 2

n'est que d'ampleur constante, et la complexité temporelle de la transformation est :

T(n) = O(1)

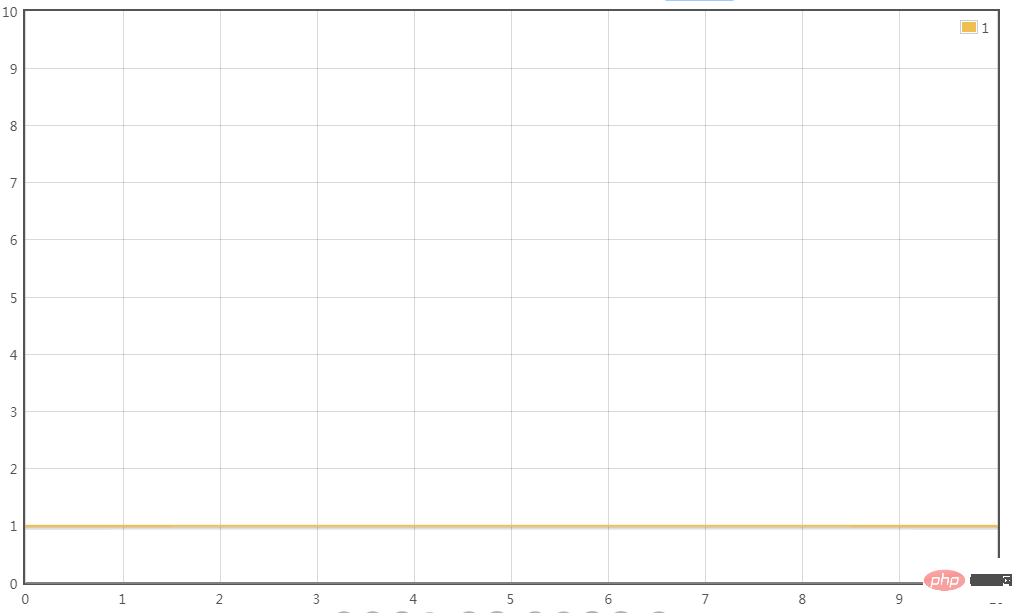
Scénario 4 :

T(n) = 0,5n^ 2 + 0,5n

Le terme d'ordre le plus élevé est 0,5n^2, en omettant le coefficient 0,5, la complexité temporelle de la transformation est :

T(n ) = O(n^2)

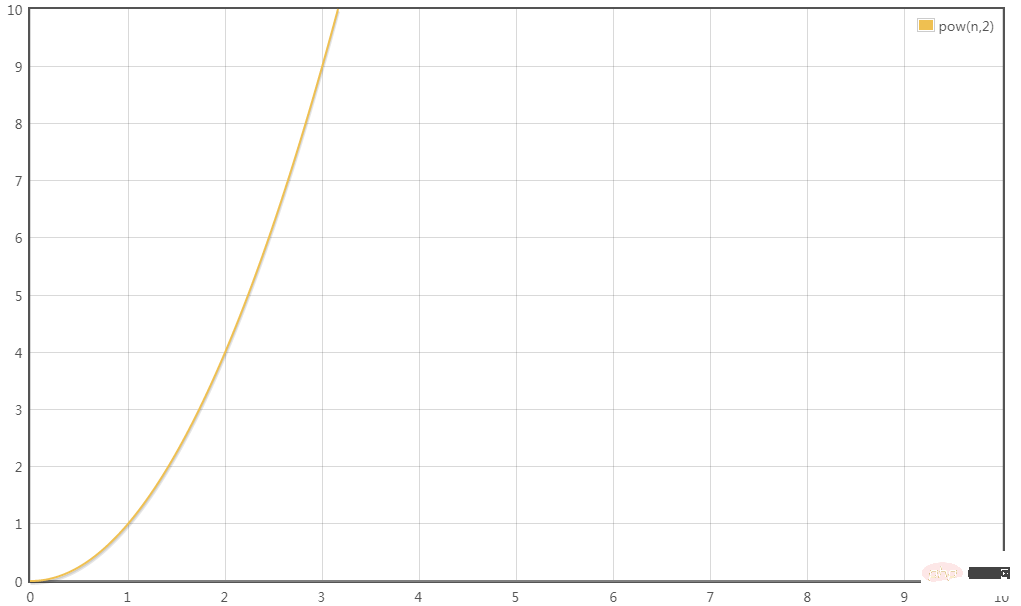
Laquelle de ces quatre complexités temporelles prend le plus de temps et qui gagne du temps ? Après une petite réflexion, vous pouvez arriver à la conclusion :

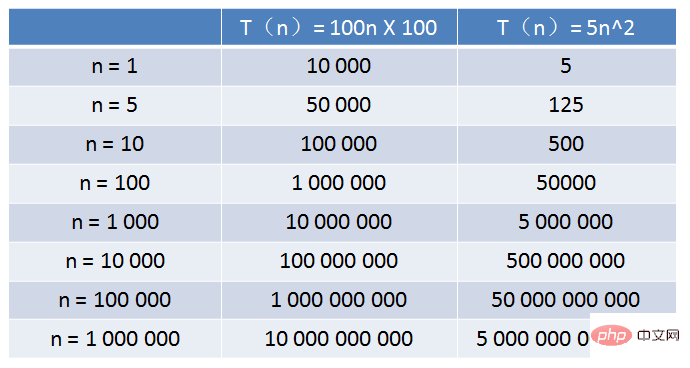
O(1)

Dans le monde de la programmation Il existe différents algorithmes En plus des quatre scénarios mentionnés ci-dessus, il existe de nombreuses formes différentes de complexité temporelle, telles que :

O(nlogn), O(n^3), O(m). *n ), O(2^n), O(n!)

À l'avenir, lorsque nous voyagerons dans l'océan du code, nous continuerons à rencontrer des algorithmes avec la complexité temporelle ci-dessus.

Énorme différence dans la complexité temporelle

Donnons un exemple :

L'échelle de temps relative de l'algorithme A est T(n) = 100n, et la complexité temporelle est O(n)

Le temps relatif de l'algorithme B L'échelle est T(n) = 5n^2 et la complexité temporelle est O(n^2)

L'algorithme A s'exécute sur un vieil ordinateur chez Xiao Hui et l'algorithme B s'exécute sur un certain superordinateur. La vitesse de fonctionnement est 100 fois supérieure à celle des anciens ordinateurs.

Alors, à mesure que la taille d'entrée n augmente, lequel des deux algorithmes s'exécute plus rapidement ?

Comme le montre le tableau, lorsque la valeur de n est très petite, le temps d'exécution de l'algorithme A est beaucoup plus long que celui de l'algorithme B lorsque la valeur ; de n atteint environ 1 000. Les temps d'exécution de l'algorithme A et de l'algorithme B sont proches ; lorsque la valeur de n devient de plus en plus grande, atteignant cent mille ou un million, les avantages de l'algorithme A commencent à apparaître, tandis que l'algorithme B devient plus lent. et plus lentement, et l'écart devient de plus en plus évident.

C'est la différence causée par différentes complexités temporelles.

Si vous souhaitez connaître plus de tutoriels techniques, assurez-vous de faire attention au Site Web PHP chinois !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!