Structures de données : quelle est la différence entre un graphique et un arbre

Les graphiques et les arbres sont tous deux les structures de données non linéaires les plus courantes, alors quelles sont les différences entre elles ? L'article suivant expliquera la différence entre les graphiques et les arbres. J'espère qu'il sera utile à tout le monde.

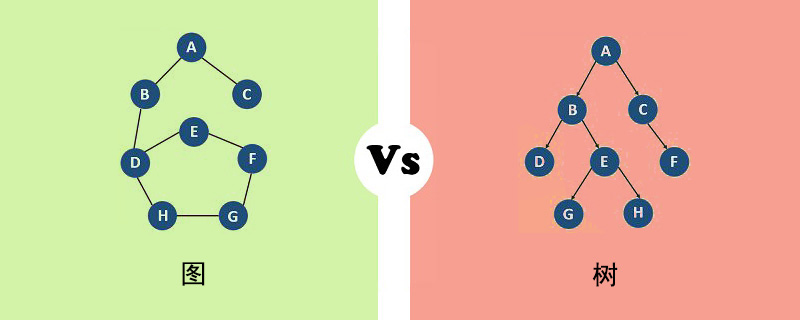
Graphique

Le thème est composé de deux ensembles V et E, où V est fini est un ensemble de sommets non vide, et E est un ensemble d'arêtes fini non vide. Il possède les attributs suivants :

1. Un sommet représente un nœud dans le graphe et peut être connecté à n'importe quel nombre d'autres sommets à l'aide d'arêtes.

2. Deux sommets adjacents sont reliés par une arête. L'arête peut être bidirectionnelle ou directionnelle ; l'arête peut également être pondérée.

3. Tout graphique peut être exprimé comme suit : G = {V, E}.

Par exemple :

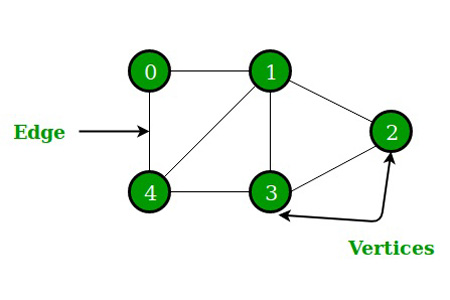
Alors : G = {{V1, V2, V3, V4, V5}, {E1, E2, E3, E4, E5 , E6, E7}}

Arbre

Un arbre est un ensemble fini K contenant n (n>0) nœuds, et a les propriétés suivantes :

1. Il y a un nœud désigné au sommet de l'arbre, qui est appelé la racine de l'arbre.

2. Les éléments de données restants sont divisés en sous-ensembles disjoints, appelés sous-arbres.

3. La hauteur de l'arbre s'étend vers le bas.

4. L'arbre doit être connecté, ce qui signifie qu'il doit y avoir un chemin d'une racine à tous les autres nœuds.

5. Il ne contient aucune boucle.

6. L'arbre a n-1 côtés.

Par exemple :

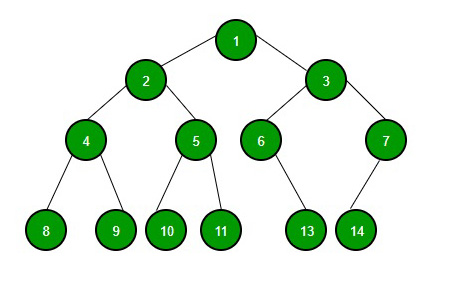
Différence entre le graphique et l'arbre

Graphique

1. Chaque nœud du graphique peut avoir n'importe quel nombre d'arêtes, et les arêtes peuvent être unidirectionnelles ou bidirectionnelles.

2. Il n'y a pas de concept de nœud racine nommé racine dans le graphique.

3. Les graphiques peuvent avoir des boucles et des auto-boucles

4 Dans un graphique, il n'y a pas de nombre prédéfini d'arêtes, cela dépend du graphique.

5. Le graphique est la structure du modèle de réseau.

Arbre

1. Un arbre régulier se compose de nœuds avec n'importe quel nombre de nœuds enfants mais dans le cas d'un arbre binaire, chaque nœud peut en avoir jusqu'à deux ; nœuds enfants. Il n’y a qu’une seule arête entre deux nœuds.

2. Il existe un nœud unique nommé racine dans l'arborescence.

3. Les arbres ne peuvent pas avoir de cycles ou d'auto-boucles

4 Les arbres peuvent avoir n-1 arêtes.

5. L'arbre est une structure hiérarchique.

Ce qui précède représente l’intégralité du contenu de cet article, j’espère qu’il sera utile à l’étude de chacun. Pour un contenu plus passionnant, vous pouvez prêter attention aux colonnes de didacticiels pertinentes du site Web PHP chinois ! ! !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!