Maison >interface Web >js tutoriel >Comment implémenter des algorithmes de tri et de recherche en JS
Comment implémenter des algorithmes de tri et de recherche en JS
- 青灯夜游avant
- 2019-03-28 10:12:162602parcourir
Le contenu de cet article est de présenter comment utiliser JS pour implémenter des algorithmes de tri et de recherche. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.
1. Préparation
Avant d'entrer dans le sujet, préparez quelques fonctions de base
(1) Échangez deux éléments du tableau
function swap(arr, sourceIndex, targetIndex) {
let temp = arr[sourceIndex];
arr[sourceIndex] = arr[targetIndex];
arr[targetIndex] = temp;
}
(2) Générez rapidement un tableau de 0~N
function createArr(length) {
return Array.from({length}, (_, i) => i);
}
(3) Fonction Shuffle
La fonction de lecture aléatoire peut rapidement perturber le tableau. Les utilisations courantes incluent la commutation de l'ordre de lecture de la musique
function shuffle(arr) {
for (let i = 0; i <h2><strong>2. Tri</strong></h2><p>Algorithmes de tri courants. peut Divisé en deux grandes catégories : </p>
-
Tri par comparaison : Déterminer l'ordre relatif entre les éléments par comparaison. Puisque sa complexité temporelle ne peut pas dépasser
O(nlogn), il est également appelé Non-. tri par comparaison temporelle linéaire - Tri sans comparaison : il ne détermine pas l'ordre relatif entre les éléments par comparaison. Il peut franchir la limite inférieure temporelle du tri basé sur la comparaison et s'exécuter de manière linéaire. temps, donc Également connu sous le nom de tri non comparatif en temps linéaire
Dans cet article, seules quelques méthodes de tri de tri comparatif sont présentées
2.1 Tri à bulles
Le tri à bulles est le plus simple de tous les algorithmes de tri et constitue généralement la méthode d'introduction pour nous permettre d'apprendre le tri. Cependant, du point de vue du temps d’exécution, le tri à bulles est la pire méthode de tri.
Core : comparez deux éléments adjacents et si le premier est supérieur au second, échangez-les . Les éléments sont déplacés vers le haut dans le bon ordre, comme si des bulles remontaient à la surface, d'où le nom de tri à bulles
GIF :
Remarque : Le premier niveau parcourt pour trouver la valeur maximale des éléments restants et atteint la position spécifiée [fait ressortir la valeur maximale à son tour]
Code :
function bubbleSort(arr) {
const len = arr.length;
for (let i = 0; i arr[j + 1]) { // 比较相邻元素
swap(arr, j, j + 1);
}
}
}
return arr;
}
2.2 Tri par sélection
Le tri par sélection est un algorithme de tri par comparaison sur place.
Noyau : recherchez d'abord le plus petit élément de la séquence non triée et stockez-le à la position de départ de la séquence triée. Ensuite, continuez à trouver le plus petit élément parmi les éléments non triés restants et placez-le dans le. séquence triée à la fin de. Et ainsi de suite, jusqu'à ce que tous les éléments soient triés
Gif :
Remarque : découvertes de parcours de première couche l'index de la valeur minimale des éléments restants, puis échange la position actuelle et la valeur minimale de l'indice [trouver la valeur minimale à son tour]
Code :
function selectionSort(arr) {
const len = arr.length;
let minIndex;
for (let i = 0; i arr[j]) {
minIndex = j; // 寻找最小值对应的索引
}
}
if (minIndex === i) continue;
swap(arr, minIndex, i);
}
return arr;
}
2.3 Tri par insertion
L'ordre de comparaison du tri par insertion est différent du tri à bulles et du tri par sélection. L'ordre de comparaison du tri par insertion est une comparaison directe de l'élément actuel.
Core : En construisant une séquence ordonnée, pour les données non triées, scanner d'arrière en avant dans la séquence triée, trouver la position correspondante et insérer
GIF :
Remarque : À partir du deuxième élément, comparez vers l'avant afin de vous assurer que la séquence précédente de l'élément actuel est dans l'ordre
Code :
function insertionSort(arr) {
const len = arr.length;
let current, pointer;
for (let i = 1; i = 0 && current <h3><strong>2.4 Tri par fusion</strong></h3><p>Par rapport aux trois algorithmes de tri ci-dessus, tri par fusion et rapide trier C'est plus réalisable en pratique (dans la quatrième section, nous comparerons ces algorithmes de tri par complexité pratique) La classe </p> de <blockquote>
<code>JavaScript</code><code>Array</code> définit une fonction <code>sort</code> (<code>Array.prototype.sort</code>) est utilisé pour trier le tableau <code>JavaScript</code>. <code>ECMAScript</code>Il n'y a pas de définition de l'algorithme de tri utilisé, les fabricants de navigateurs peuvent donc implémenter l'algorithme eux-mêmes. Par exemple, <code>Mozilla Firefox</code> utilise le <strong>tri par fusion</strong> comme implémentation de <code>Array.prototype.sort</code>, tandis que <code>Chrome</code> utilise une variante du <strong>tri rapide</strong> </blockquote><p><strong>tri par fusion. une sorte de <code>分治算法</code>. L'idée est de diviser le tableau d'origine en tableaux plus petits jusqu'à ce que chaque petit tableau n'ait qu'une seule position, puis de fusionner les petits tableaux en tableaux plus grands jusqu'à ce qu'il n'y ait qu'un seul grand tableau trié. Par conséquent, vous devez utiliser le noyau <code>递归</code></strong></p><p><strong> : trier par fusion, diviser en tableaux gauche et droit, les trier séparément, puis fusionner </strong></p><p style="text-align: left;"><strong>animation :</strong></p><p style="text-align: center;"><img src="https://img.php.cn/upload/image/174/628/728/1553738670821848.gif" title="1553738670821848.gif" alt="Comment implémenter des algorithmes de tri et de recherche en JS"></p><p><strong>注意:递归中最小的左右数组比较为单个元素的数组,因此在较上层多个元素对比时,左右两个数组一定是顺序的</strong></p><p><strong>代码:</strong></p><pre class="brush:php;toolbar:false">function mergeSort(arr) {
const len = arr.length;
if (len right[0]) {
ret.push(right.shift());
} else {
ret.push(left.shift());
}
}
while (left.length) {
ret.push(left.shift());
}
while (right.length) {
ret.push(right.shift());
}
return ret;
}2.5 快速排序
快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn),且它的性能通常比其他的复 杂度为O(nlogn)的排序算法要好。和归并排序一样,快速排序也使用分治的方法,将原始数组分为较小的数组
核心:分治算法,以参考值为界限,将比它小的和大的值拆开
动图:
注意:每一次遍历筛选出比基准点小的值
代码:
function quickSort(arr, left = 0, right = arr.length - 1) {
// left和right默认为数组首尾
if (left <h2><strong>三、搜索算法</strong></h2><h3><strong>3.1 顺序搜索</strong></h3><p>顺序或线性搜索是最基本的搜索算法。它的机制是,将每一个数据结构中的元素和我们要找的元素做比较。<strong>顺序搜索是最低效的一种搜索算法。</strong></p><pre class="brush:php;toolbar:false">function findItem(item, arr) {
for (let i = 0; i <h3><strong>3.2 二分搜索</strong></h3><p>二分搜索要求被搜索的数据结构已排序。以下是该算法遵循的步骤:</p><ol>
<li>选择数组的中间值</li>
<li>如果选中值是待搜索值,那么算法执行完毕</li>
<li>如果待搜索值比选中值要小,则返回步骤1在选中值左边的子数组中寻找</li>
<li>如果待搜索值比选中值要大,则返回步骤1在选中值右边的子数组中寻找</li>
</ol><pre class="brush:php;toolbar:false">function binarySearch(item, arr) {
arr = quickSort(arr); // 排序
let low = 0;
let high = arr.length - 1;
let mid;
while (low item) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}四、算法复杂度
4.1 理解大O表示法
大O表示法用于描述算法的性能和复杂程度。分析算法时,时常遇到一下几类函数
(1)O(1)
function increment(num){
return ++num;
}执行时间和参数无关。因此说,上述函数的复杂度是O(1)(常数)
(2)O(n)
以顺序搜索函数为例,查找元素需要遍历整个数组,直到找到该元素停止。函数执行的总开销取决于数组元素的个数(数组大小),而且也和搜索的值有关。但是函数复杂度取决于最坏的情况:如果数组大小是10,开销就是10;如果数组大小是1000,开销就是1000。这种函数的时间复杂度是O(n),n是(输入)数组的大小
(3)O(n2)
以冒泡排序为例,在未优化的情况下,每次排序均需进行n*n次执行。时间复杂度为O(n2)
时间复杂度O(n)的代码只有一层循环,而O(n2)的代码有双层嵌套循环。如 果算法有三层遍历数组的嵌套循环,它的时间复杂度很可能就是O(n3)
4.2 时间复杂度比较
(1)常用数据结构时间复杂度
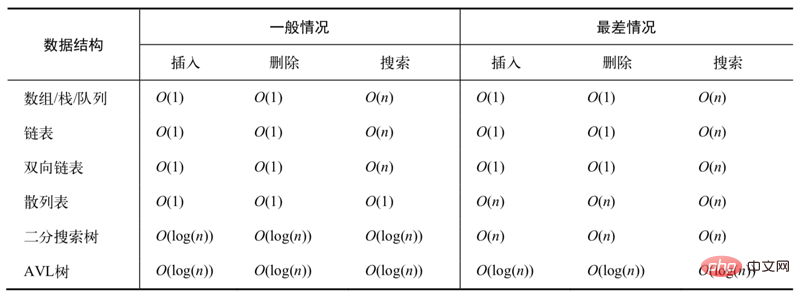
(2)排序算法时间复杂度
相关视频教程推荐:《JavaScript教程》
以上就是本篇文章的全部内容,希望能对大家的学习有所帮助。更多精彩内容大家可以关注php中文网相关教程栏目!!!
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!








