Introduction aux méthodes d'implémentation d'algorithmes récursifs en JavaScript

Cet article vous présente la méthode d'implémentation d'algorithmes récursifs en JavaScript. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

Regardons d’abord la définition. Un algorithme récursif convertit un problème en sous-problèmes du même type, de taille réduite, et chaque sous-problème est résolu à l'aide du même algorithme. De manière générale, un algorithme récursif est une fonction qui s'appelle elle-même pour résoudre ses sous-problèmes.

Caractéristiques de l'algorithme récursif :

1. s'appelle pendant le processus de fonction.
2. Pendant le processus récursif, il doit y avoir une condition claire pour déterminer la fin de la récursivité, c'est-à-dire la sortie récursive.
3. L'algorithme récursif est simple mais inefficace et n'est généralement pas recommandé comme algorithme recommandé.

Les explications ci-dessus sont tirées de l'Encyclopédie Baidu, et elles sont très claires. Veuillez les considérer attentivement avec des exemples.

　Factorial

　Description du problème : n = n*(n-1)*...2*1

Implémentation du code :

Lorsque nous rencontrons le problème, nous pouvons d'abord réduire l'échelle à des sous-problèmes similaires selon la définition. Par exemple, n! est égal à n* (n-1)!, alors (n-1) = (n-1)*(n-2)!. Appuyez dans cet ordre jusqu'à la sortie de if. arguments.callee est utilisé ici pour empêcher un couplage étroit des noms de fonctions. Ici, il équivaut à factorial(n-1). La mise en œuvre de la fonction est-elle simple et claire ? Bien sûr, comme l'ampleur du problème est simple, il peut être implémenté à l'aide de boucles. Vous pouvez l'essayer.

Séquence de Fibonacci

　Description du problème : 1, 1, 2, 3, 5, 8, 13, 21, 34, ... .... Trouvez le nième nombre.

Implémentation du code :

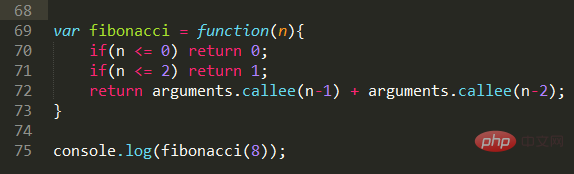
En fait, il est très simple de mettre en œuvre l'idée tout de suite. Grâce à l'analyse, nous pouvons obtenir le nième nombre, qui est la somme des deux premiers nombres. Grâce à cela, nous pouvons continuer à obtenir les deux premiers nombres dont nous avons besoin par récursion jusqu'à ce que la condition n

　Le problème de prendre les escaliers

Description du problème : Il y a n marches dans les escaliers Vous pouvez monter 1 marche en une seule marche. ou 2 étapes en une seule étape. Ou niveau 3, comptez le nombre de mouvements différents.

Implémentation du code :

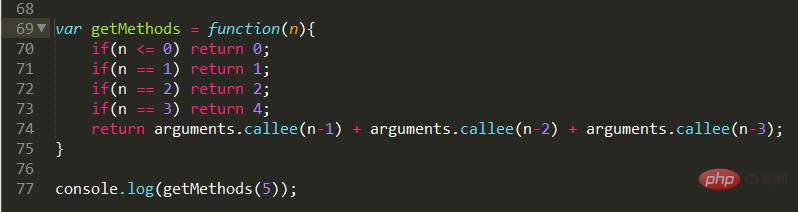
Il s'agit en fait d'une implémentation de la séquence de Fibonacci. Lorsque nous analysons, nous pouvons le convertir en problèmes de sous-classes à petite échelle. Lorsque vous atteignez la dernière marche de l’échelle désignée, il peut y avoir trois situations : une est une marche plus haut, deux est deux marches plus haut et trois est trois marches plus haut. La méthode globale est donc F(n) = F(n-1) + F(n-2) + F(n-3). Ensuite, naturellement, cela devient leur propre petit calcul, et le cycle continue jusqu'à ce que la condition de jugement se produise.

　Plus grand diviseur commun

　Description du problème : Étant donné deux nombres, si les deux nombres sont égaux, le plus grand diviseur commun est lui-même. S'ils ne sont pas égaux, prenez la valeur absolue de la soustraction des deux nombres et comparez-la avec le plus petit des deux nombres. S'ils sont égaux, c'est le plus grand dénominateur commun. S'ils ne sont pas égaux, continuez l'algorithme ci-dessus. jusqu'à ce qu'ils soient égaux.

Implémentation du code :

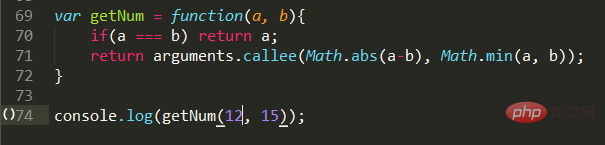
Il n'y a rien à dire, il suffit de l'implémenter comme l'exige la description du problème. La sortie de la récursion est que a est égal à b.

Tour de Hanoï

Description du problème : Tout le monde y a plus ou moins joué, je n'entrerai donc pas dans les détails ici.

Implémentation du code :

Avant de réaliser l'essence de la récursivité, j'étais simplement intrigué par ce problème. Je n’arrête pas de me demander : comment savoir où aller ensuite ? Plus tard, j’ai réalisé que j’étais en fait plus préoccupé par la façon de procéder pour le dernier. Comment dites-vous cela ? Nous pouvons penser dès le début, si nous n’avons qu’un seul disque, nous pouvons le faire passer à la colonne C ou à la colonne B. Bien entendu, cela peut également être réalisé avec deux disques. 3 disques, c'est bien. Parlons ensuite de la situation de 4 disques. Pour compléter les quatre disques, le disque de A doit être entièrement transféré vers C. Nous mettons les trois premiers disques dans leur ensemble sur B, puis le quatrième disque peut être déplacé vers C. Ensuite, nous mettons les trois premiers disques sur C, et cela a réussi. Les trois premiers jeux peuvent être traités comme un nouveau jeu, et les deux premiers jeux peuvent être traités comme un tout, et ainsi de suite. De cette façon, nous n'avons qu'à nous soucier des grandes choses globales, et d'autres choses peuvent être résolues en problèmes à petite échelle.

DichotomieTri rapide

Description du problème : utilisez la méthode de dichotomie pour trier un tableau de petit à grand.

Implémentation du code :

　

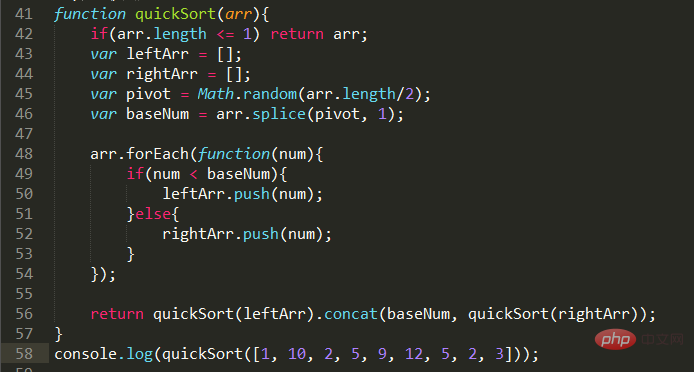
Eh bien... c'est la deuxième fois que j'écris ceci. Cette fois, l'implémentation de la récursivité est beaucoup plus claire que la dernière fois. En fait, il s'agit aussi de réduire la grande échelle à la petite échelle, de se soucier d'un grand tout et de le laisser continuer à être réduit à la petite échelle pour le calcul. Vous pouvez consulter l'essai original pour plus de détails.

Récursion de l'arborescence DOM

Description du problème : obtenir le tagName de tous les nœuds parents d'un nœud

Implémentation du code :

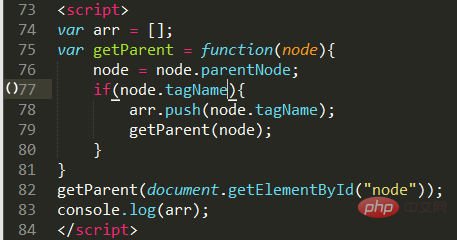
Vous pouvez probablement le comprendre et vous ne direz rien. Comparé aux précédents Tower of Hanoi et Quick Sort, celui-ci est assez simple, mais il est le plus proche de l’application pratique de notre JavaScript.

Cet article est terminé ici. Pour un contenu plus passionnant, vous pouvez faire attention à la colonne JavaScript Video Tutorial du site Web PHP chinois !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!