Introduction à la file d'attente circulaire Java (exemple de code)

Cet article vous présente une introduction aux files d'attente circulaires Java (exemples de code). Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

Afin de résoudre les problèmes causés par les files d'attente de tableaux, cet article vous présente les files d'attente circulaires.

Illustration de l'analyse d'idées

Oh ma parole, car l'auteur n'est pas très doué pour faire en sorte que les images publiées aient des effets d'animation, comme le déplacement ou la suppression éléments (après tout, c'est plus intuitif pour tout le monde). L'auteur ne peut vous aider à comprendre le principe de mise en œuvre qu'à travers des images statiques ici. J'espère que vous ne serez pas offensé. Si quelqu'un sait comment le faire, veuillez partager votre sagesse dans le. zone de commentaires.

Ici, nous déclarons un tableau d'une capacité de 8 et marquons l'index 0-7, puis utilisons front et tail pour représenter la file d'attente, la tête et la fin de la file d'attente ; dans l'image ci-dessous, les positions de front et tail pointent initialement vers la position de l'index 0, ce qui signifie que lorsque front == tai la <font color="'red'"></font>file d'attente est vide Tout le monde doit garder cela à l'esprit, dans afin de distinguer les conditions critiques lorsque la file d'attente est presque pleine, qui seront introduites ultérieurement

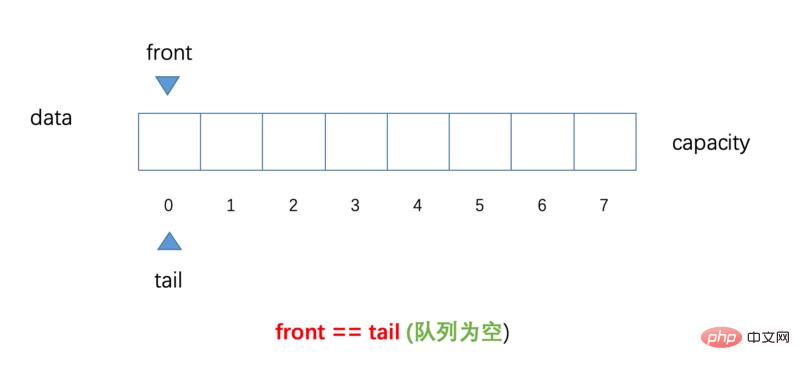
Afin que chacun puisse mieux comprendre le contenu suivant, ici, je va l'expliquer brièvement

front : Représente la tête de la file d'attente, pointant toujours vers le premier élément de la file d'attente (lorsque la file d'attente est vide, front pointe vers la position d'index 0)

tail : Représente la fin de la file d'attente, pointant toujours vers la position suivante du dernier élément de la file d'attente

les éléments entrent dans la file d'attente, maintiennent la position de tail, et effectuer des opérations tail++. Les éléments

sont retirés de la file d'attente et maintenus. À la position de front, effectuez l'opération front++ Comme mentionné ci-dessus, lorsque les éléments sont mis en file d'attente et retirés de la file d'attente, il s'agit simplement d'une opération ++. maintenir les positions de tail et front. Ce n'est en fait pas rigoureux, la position correcte pour maintenir la queue doit être de (queue + 1) % de capacité. C'est pourquoi on l'appelle une file d'attente circulaire. Sachons-le ici d'abord. Je ne l'expliquerai pas pour le moment. Peu importe si vous comprenez, je pense que tout le monde le saura plus tard.

Jetons un coup d'oeil. Maintenant, si un élément a rejoint la file d'attente, le diagramme actuel :

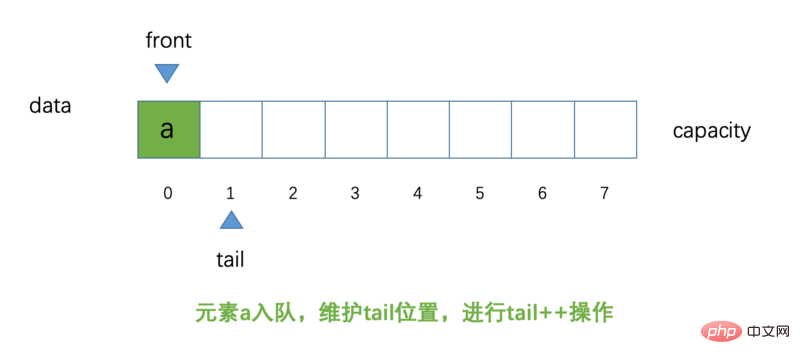
Nous voyons maintenant cet élément a rejoint la file d'attente, notre La position pointée par tail a changé et l'opération ++ a été effectuée, mais la position de front n'a pas changé et pointe toujours vers la position d'index 0. Rappelez-vous ce que l'auteur a dit plus haut, la position de front pointe toujours vers le premier position dans la file d'attente. élément, la position de la queue pointe toujours vers la position suivante du dernier élément dans la file d'attente

Maintenant, ajoutons quelques éléments supplémentaires b, c, d, e à la file d'attente. Jetez un oeil à ceci Le diagramme schématique de l'époque :

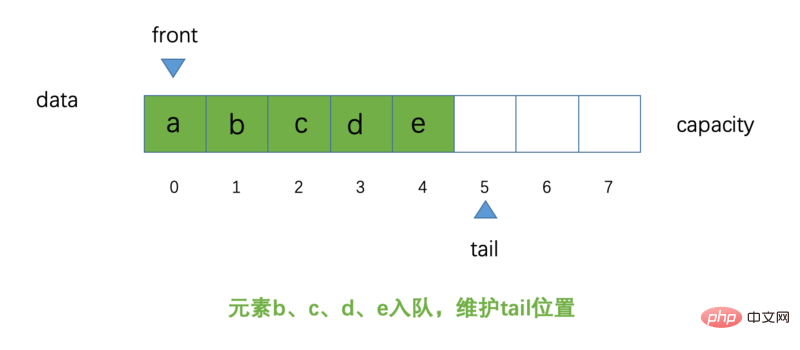
Je crois que tout le monde sait que le diagramme schématique est comme ça, il semble qu'il y en ait pas beaucoup de changements (ne vous inquiétez pas, l'auteur est là pour faciliter la compréhension de chacun) Qu'est-ce qu'une file d'attente circulaire exactement ? S'il vous plaît, pardonnez-moi O(∩_∩)O ! le fonctionnement des éléments entrant dans la file d'attente, regardons le retrait des éléments de la file d'attente. À quoi ressemble l'opération ?

L'élément est retiré de la file d'attente. Le diagramme schématique est le suivant :

a

Maintenant, l'élément a a été retiré de la file d'attente et la position de l'avant. pointe vers l'index 1 Position, désormais tous les éléments du tableau n'ont plus besoin d'avancer d'une position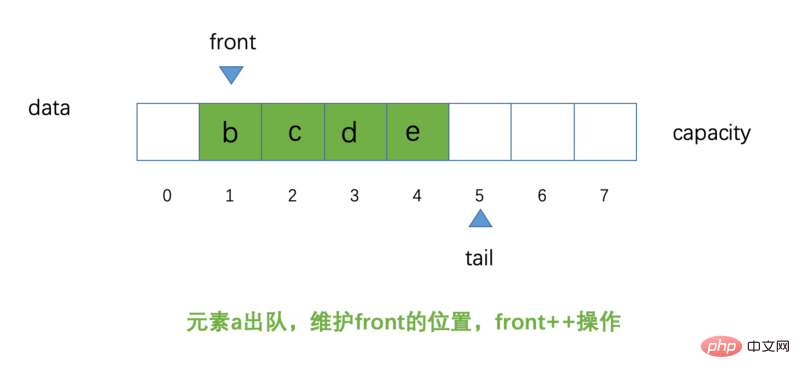

C'est la même chose que notre file d'attente de tableau (notre file d'attente de tableau nécessite que les éléments soient retirés de la file d'attente et les éléments suivants doivent se déplacer une position en avant) Complètement différent, il suffit de changer la direction du front. L'opération O(n) précédente est devenue une opération O(1)

Nous retirons l'élément b de la file d'attente, le diagramme schématique. est la suivante :

À ce stade, certains amis peuvent se demander pourquoi on appelle cela une file d'attente circulaire ? Alors maintenant, essayons. Nous laissons les éléments f et g rejoindre respectivement la file d'attente. Le schéma schématique à ce moment est le suivant :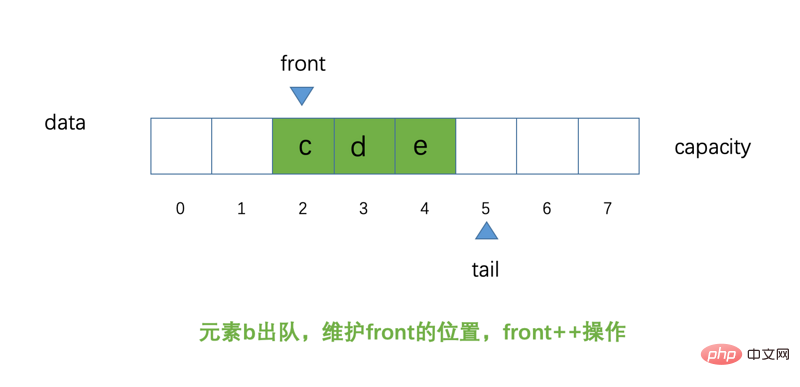

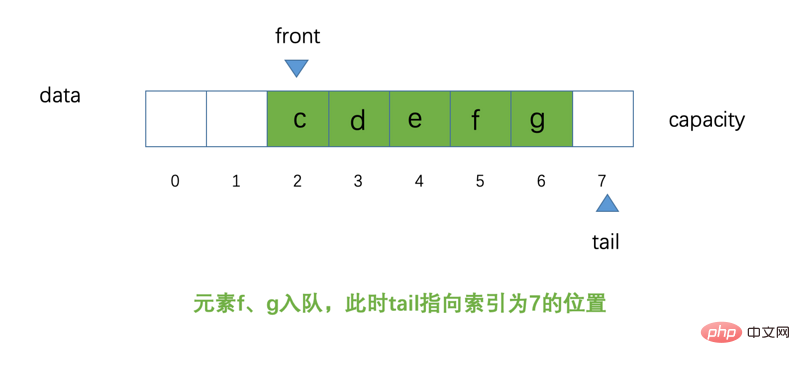Il n'y a toujours pas de changement. selon l'inspection visuelle. Si à ce moment-là, nous laissons ajouter un autre élément h à la file d'attente, alors la question se pose : comment doit-on pointer la position de notre queue ? Le schéma schématique est le suivant :

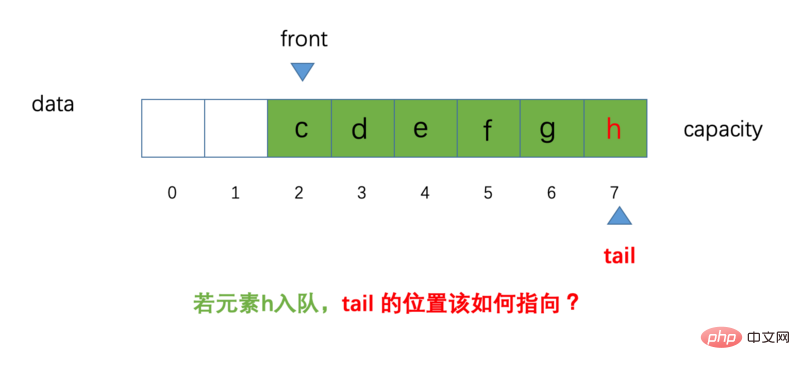
Selon ce que nous avons dit précédemment, les éléments sont mis en file d'attente : maintenez la position de tail et effectuez l'opération tail++. À ce moment, notre queue a pointé vers la position avec l'index 7. Si nous. Il est évidemment impossible d'effectuer une opération ++ sur tail (tableau hors limites)

Des amis prudents constateront que notre file d'attente n'est pas pleine en ce moment, et qu'il reste encore deux positions (c'est parce qu'après notre les éléments sont retirés de la file d'attente), l'espace actuel n'est pas expulsé par les éléments suivants), vous pouvez imaginer notre tableau comme un anneau, alors la position après l'index 7 est l'index 0

Comment pouvons-nous calculer à partir de la position de l'index 7 À la position de l'index 0, nous avons déjà parlé d'opérations tail++. L'auteur a également souligné au début que cela n'est pas rigoureux. Cela devrait être (tail + 1) % de capacité, ce qui devient (7 + 1) %. 8 est égal à 0.

Donc, si nous laissons l'élément h rejoindre la file d'attente à ce moment-là, alors notre queue pointera vers la position d'index 0. Le diagramme schématique est le suivant :

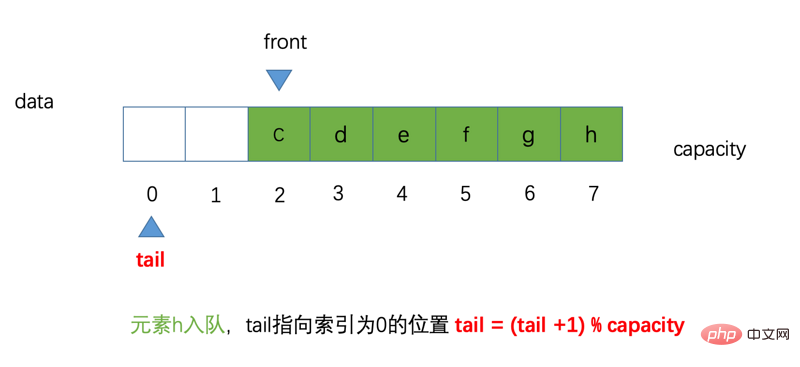
Supposons qu'un nouvel élément k soit maintenant ajouté à la file d'attente, alors la position de la queue est égale à (queue + 1) % de capacité, soit (0 + 1) % 8. S'il est égal à 1, il pointe vers la position d'index 1

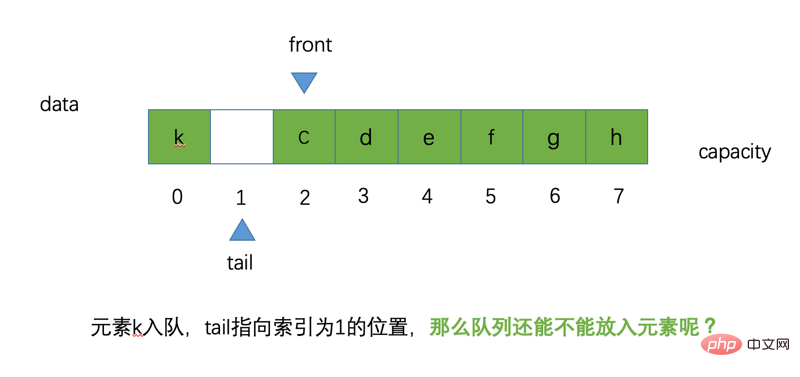
Alors la question est : notre file d'attente circulaire peut-elle toujours mettre les éléments en file d'attente ? Analysons-le. L'image montre que nous avons toujours une position d'espace vide avec l'indice 0, qui est la position pointée par tail à ce moment

Selon la logique précédente, en supposant qu'un nouvel élément puisse être mis dedans. maintenant, notre queue effectue (queue +1) % de calcul de capacité et le résultat est 2 (si l'élément est ajouté avec succès à la file d'attente, la file d'attente est pleine à ce moment), à ce moment nous constaterons que le devant représentant la tête de la file d'attente pointe également vers la position d'index 2

Si le nouvel élément est ajouté avec succès à la file d'attente, notre queue est également égale à 2, alors elle devient tail == front Au début nous l'avons mentionné. lorsque la file d'attente est vide, tail == front, et maintenant ? , si tail est également égal à front lorsque la file d'attente est pleine, alors nous ne pouvons pas faire la distinction entre la collecte lorsque la file d'attente est pleine et la collecte lorsque la file d'attente est vide

Par conséquent, dans la file d'attente circulaire, nous perdons toujours un espace, Pour faire la distinction entre le moment où la file d'attente est pleine et le moment où la file d'attente est vide, c'est-à-dire lorsque (queue + 1) % de capacité == avant, cela signifie que la file d'attente est pleine, et quand front == tail, cela signifie que la file d'attente est vide.

Après avoir compris le principe de mise en œuvre de la file d'attente circulaire, implémentons-la avec du code.

Implémentation du code

Définition de l'interface : Queue

public interface Queue<e> {
    /**
     * 入队
     *
     * @param e
     */
    void enqueue(E e);

    /**
     * 出队
     *
     * @return
     */
    E dequeue();

    /**
     * 获取队首元素
     *
     * @return
     */
    E getFront();

    /**
     * 获取队列中元素的个数
     *
     * @return
     */
    int getSize();

    /**
     * 判断队列是否为空
     *
     * @return
     */
    boolean isEmpty();
}</e>

Implémentation de l'interface : LoopQueue

public class LoopQueue<e> implements Queue<e> {
    /**
     * 承载队列元素的数组
     */
    private E[] data;
    /**
     * 队首的位置
     */
    private int front;
    /**
     * 队尾的位置
     */
    private int tail;
    /**
     * 队列中元素的个数
     */
    private int size;

    /**
     * 指定容量，初始化队列大小
     * (由于循环队列需要浪费一个空间，所以我们初始化队列的时候，要将用户传入的容量加1)
     *
     * @param capacity
     */
    public LoopQueue(int capacity) {
        data = (E[]) new Object[capacity + 1];
    }

    /**
     * 模式容量，初始化队列大小
     */
    public LoopQueue() {
        this(10);
    }


    @Override
    public void enqueue(E e) {
        // 检查队列为满
        if ((tail + 1) % data.length == front) {
            // 队列扩容
            resize(getCapacity() * 2);
        }
        data[tail] = e;
        tail = (tail + 1) % data.length;
        size++;
    }


    @Override
    public E dequeue() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        // 出队元素
        E element = data[front];
        // 元素出队后，将空间置为null
        data[front] = null;
        // 维护front的索引位置(循环队列)
        front = (front + 1) % data.length;
        // 维护size大小
        size--;

        // 元素出队后，可以指定条件，进行缩容
        if (size == getCapacity() / 2 && getCapacity() / 2 != 0) {
            resize(getCapacity() / 2);
        }
        return element;
    }

    @Override
    public E getFront() {
        if (isEmpty()) {
            throw new IllegalArgumentException("队列为空");
        }
        return data[front];
    }

    @Override
    public int getSize() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return front == tail;
    }


    // 队列快满时，队列扩容；元素出队操作，指定条件可以进行缩容
    private void resize(int newCapacity) {
        // 这里的加1还是因为循环队列我们在实际使用的过程中要浪费一个空间
        E[] newData = (E[]) new Object[newCapacity + 1];
        for (int i = 0; i <p>Test Classe : LoopQueueTest</p>
<pre class="brush:php;toolbar:false">public class LoopQueueTest {
    @Test
    public void testLoopQueue() {
        LoopQueue<integer> loopQueue = new LoopQueue();
        for (int i = 0; i <h5>Résultat du test : </h5>
<pre class="brush:php;toolbar:false">原始队列: LoopQueue{【队首】data=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=0, tail=10, size=10, capacity=10}
元素0出队: LoopQueue{【队首】data=[null, 1, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=1, tail=10, size=9, capacity=10}
元素1出队: LoopQueue{【队首】data=[null, null, 2, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=2, tail=10, size=8, capacity=10}
元素2出队: LoopQueue{【队首】data=[null, null, null, 3, 4, 5, 6, 7, 8, 9, null]【队尾】, front=3, tail=10, size=7, capacity=10}
元素3出队: LoopQueue{【队首】data=[null, null, null, null, 4, 5, 6, 7, 8, 9, null]【队尾】, front=4, tail=10, size=6, capacity=10}
元素4出队,发生缩容: LoopQueue{【队首】data=[5, 6, 7, 8, 9, null]【队尾】, front=0, tail=5, size=5, capacity=5}
队首元素：5

Adresse du référentiel GitHub du code de la version complète : Structure de données de la version Java - file d'attente (file d'attente de boucle)

Cet article est terminé ici. Pour un contenu plus passionnant, vous pouvez faire attention à la colonne Java Video Tutorial du site Web PHP chinois !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!