Maison >développement back-end >Tutoriel Python >Tutoriel de reconnaissance de code de vérification Python : segmentation d'images à l'aide de la méthode de projection et de la méthode du domaine connecté
Tutoriel de reconnaissance de code de vérification Python : segmentation d'images à l'aide de la méthode de projection et de la méthode du domaine connecté
- 不言original
- 2018-06-04 16:21:202946parcourir
Cet article présente principalement le didacticiel de reconnaissance du code de vérification Python utilisant la méthode de projection et la méthode du domaine connecté pour segmenter les images. Il a une certaine valeur de référence. Maintenant, je le partage avec vous. Les amis dans le besoin peuvent s'y référer
. Avant-propos
L'article d'aujourd'hui explique principalement comment diviser le code de vérification. Les principales bibliothèques utilisées sont Pillow et l'outil de traitement d'image GIMP sous Linux. Tout d’abord, prenons un exemple avec une position et une largeur fixes, sans adhérence et sans interférence pour apprendre à utiliser Pillow pour découper des images.
Après avoir ouvert l'image à l'aide de GIMP, appuyez sur le signe plus pour agrandir l'image, puis cliquez sur Affichage->Afficher la grille pour afficher les lignes de la grille :
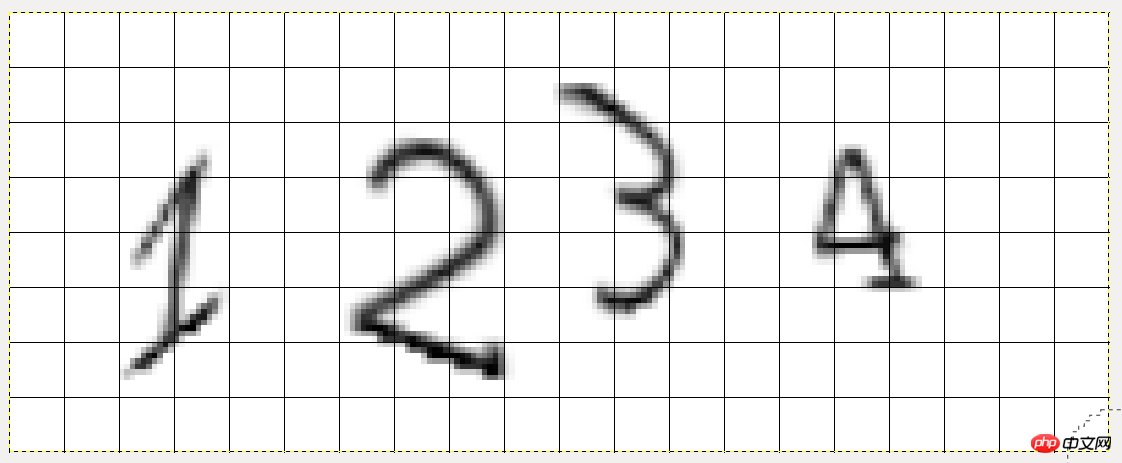
Parmi eux, la longueur du côté de chaque carré est de 10 pixels, donc les coordonnées de découpe du numéro 1 sont 20 à gauche, 20 en haut, 40 à droite et 70 en bas. Par analogie, vous pouvez connaître les positions de coupe des 3 nombres restants.
Le code est le suivant :
from PIL import Image
p = Image.open("1.png")
# 注意位置顺序为左、上、右、下
cuts = [(20,20,40,70),(60,20,90,70),(100,10,130,60),(140,20,170,50)]
for i,n in enumerate(cuts,1):
temp = p.crop(n) # 调用crop函数进行切割
temp.save("cut%s.png" % i)
Après découpe, 4 images sont obtenues :

Et si la position du personnage n'est pas fixée ? Supposons maintenant un cas de largeur de position aléatoire, sans adhérence et sans lignes interférentes.
La première méthode et la méthode la plus simple est appelée « méthode de projection ». Le principe est de projeter l'image binarisée dans le sens vertical, et de déterminer la limite de segmentation en fonction des valeurs extrêmes après projection. Ici, j'utilise toujours l'image du code de vérification ci-dessus pour la démonstration :
def vertical(img): """传入二值化后的图片进行垂直投影""" pixdata = img.load() w,h = img.size ver_list = [] # 开始投影 for x in range(w): black = 0 for y in range(h): if pixdata[x,y] == 0: black += 1 ver_list.append(black) # 判断边界 l,r = 0,0 flag = False cuts = [] for i,count in enumerate(ver_list): # 阈值这里为0 if flag is False and count > 0: l = i flag = True if flag and count == 0: r = i-1 flag = False cuts.append((l,r)) return cuts p = Image.open('1.png') b_img = binarizing(p,200) v = vertical(b_img)
Grâce à la fonction verticale, nous obtenons un graphique qui contient tous les pixels noirs sur le X- axis La position des limites gauche et droite après la projection. Comme le captcha ne gêne rien, mon seuil est fixé à 0. Concernant la fonction de binarisation, vous pouvez vous référer à l'article précédent
Le résultat est le suivant :
[(21, 37), (62, 89), (100, 122), (146, 164)]
As. vous pouvez le voir, la méthode de projection donne Les limites gauche et droite sont très proches de ce que l'on peut voir manuellement. Pour les limites supérieure et inférieure, si vous êtes paresseux, vous pouvez utiliser directement 0 et la hauteur de l'image, ou vous pouvez la projeter dans le sens horizontal. Les amis intéressés ici peuvent l'essayer eux-mêmes.
Cependant, lorsqu'il y a adhérence entre les caractères, la méthode de projection provoquera des erreurs de fractionnement, comme dans l'article précédent :

Après avoir changé le seuil à 5, les limites gauche et droite données par la méthode de projection sont :
[(5, 27), (33, 53), (59, 108)]
Évidemment les derniers 6 et 9 les chiffres ne sont pas là.
Modifiez le seuil à 7, et le résultat est :
[(5, 27), (33, 53), (60, 79), (83, 108)]
Donc pour les situations d'adhésion simples, c'est aussi possible d'ajuster le seuil résolu.
La deuxième méthode est appelée méthode de segmentation de domaine connecté CFS. Le principe est de supposer que chaque caractère est composé d'un domaine connecté distinct, autrement dit, il n'y a pas d'adhésion. Trouvez un pixel noir et commencez à juger jusqu'à ce que tous les pixels noirs connectés aient été parcourus et marqués pour déterminer la position de segmentation du caractère. . L'algorithme est le suivant :
Parcourez l'image binarisée de gauche à droite et de haut en bas Si un pixel noir est rencontré et que ce pixel n'a pas été visité auparavant, appuyez sur. ce pixel sur la pile et marquez-le comme visité.
Si la pile n'est pas vide, continuez à détecter les 8 pixels environnants et effectuez l'étape 2 ; si la pile est vide, cela signifie qu'un bloc de caractères a été détecté.
La détection se termine, déterminant ainsi un nombre de caractères.
Le code est le suivant :
import queue
def cfs(img):
"""传入二值化后的图片进行连通域分割"""
pixdata = img.load()
w,h = img.size
visited = set()
q = queue.Queue()
offset = [(-1,-1),(0,-1),(1,-1),(-1,0),(1,0),(-1,1),(0,1),(1,1)]
cuts = []
for x in range(w):
for y in range(h):
x_axis = []
#y_axis = []
if pixdata[x,y] == 0 and (x,y) not in visited:
q.put((x,y))
visited.add((x,y))
while not q.empty():
x_p,y_p = q.get()
for x_offset,y_offset in offset:
x_c,y_c = x_p+x_offset,y_p+y_offset
if (x_c,y_c) in visited:
continue
visited.add((x_c,y_c))
try:
if pixdata[x_c,y_c] == 0:
q.put((x_c,y_c))
x_axis.append(x_c)
#y_axis.append(y_c)
except:
pass
if x_axis:
min_x,max_x = min(x_axis),max(x_axis)
if max_x - min_x > 3:
# 宽度小于3的认为是噪点,根据需要修改
cuts.append((min_x,max_x))
return cuts
Le résultat de sortie après l'appel est le même que celui de l'utilisation du méthode de projection. De plus, j'ai vu qu'il existe une méthode appelée "Flood Fill" sur Internet, qui semble être la même que les domaines connectés.
Recommandations associées :
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

