Pile pratique d'application d'algorithme Python

Qu'est-ce qu'une pile ? Vous pouvez la comprendre comme une structure de données premier entré, dernier sorti (First In Last Out), une table linéaire avec des opérations limitées. L'article suivant vous présente principalement l'application pratique de stack en Python. L'article donne plusieurs exemples. Les amis dans le besoin peuvent s'y référer.

Pile (pile)

La pile est également appelée pile. Il s'agit d'une liste ordonnée spéciale, et ses opérations d'insertion et de suppression sont. tout dans la pile L'opération s'effectue par dessus et selon les règles du premier entré, premier sorti et dernier entré, premier sorti.

Comme le montre l'image ci-dessous

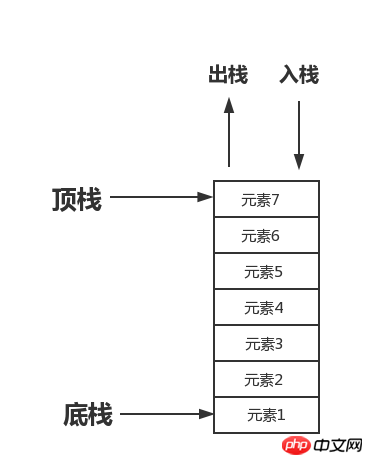
Par exemple, dans le chargeur d'une arme à feu, la première balle insérée dans le chargeur est tirée à la place, c'est la dernière balle au moment du tir, et la dernière balle insérée dans le chargeur est la première balle tirée au moment du tir.

Interface de la pile

Si vous créez une pile, vous devriez avoir l'interface suivante pour faire fonctionner la pile

接口	描述
push()	入栈
pop()	出栈
isEmpty()	判断是否为空栈
length()	获取栈的长度
getTop()	取栈顶的元素，元素不出栈

Après avoir su que la pile nécessite l'interface ci-dessus, alors en Python, la liste est similaire à une pile, et l'interface fournie est la suivante :

操作	描述
s = []	创建一个栈
s.append(x)	往栈内添加一个元素
s.pop()	在栈内删除一个元素
not s	判断是否为空栈
len(s)	获取栈内元素的数量
s[-1]	获取栈顶的元素

Exemple d'utilisation de l'interface de pile en Python :

# 创建一个栈
In [1]: s = []
# 往栈内添加一个元素
In [2]: s.append(1)
In [3]: s
Out[3]: [1]
# 删除栈内的一个元素
In [4]: s.pop()
Out[4]: 1
In [5]: s
Out[5]: []
# 判断栈是否为空
In [6]: not s
Out[6]: True
In [7]: s.append(1)
In [8]: not s
Out[8]: False
# 获取栈内元素的数量
In [9]: len(s)
Out[9]: 1
In [10]: s.append(2)
In [11]: s.append(3)
# 取栈顶的元素
In [12]: s[-1]
Out[12]: 3

Un grand nombre d'exemples

Après avoir compris les concepts de base de la pile, regardons quelques exemples supplémentaires pour faciliter notre compréhension de la pile.

Correspondance des crochets

Question

Si l'expression peut contenir trois crochets (), [], {}, l'ordre d'imbrication est Arbitraire, par exemple :

Format correct

{()[()]},[{({})}]

Format incorrect

[(]),[()),(()}

Écrire une fonction pour déterminer si la correspondance entre parenthèses d'une chaîne d'expression est correcte

Idée

1. Créer une pile vide pour stocker la parenthèse gauche qui n'a pas encore été trouvé ;

2. Chaîne de commodité, lorsque vous rencontrez un support gauche, poussez-le sur la pile, lorsque vous rencontrez un support droit, sortez un support gauche de la pile pour faire correspondre ;

3. Lors de la deuxième étape, si le support droit est rencontré lorsque la pile est vide, cela signifie que le support gauche est manquant et ne correspond pas ;

4. A la fin du parcours de la deuxième étape, la pile n'est pas vide, indiquant que le support droit est manquant et ne correspond pas

Code de solution

Il est recommandé de casser les points dans pycharm pour une meilleure compréhension

#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT = {'(', '[', '{'} # 左括号
RIGHT = {')', ']', '}'} # 右括号
def match(expr):
 """
 :param expr: 传过来的字符串
 :return: 返回是否是正确的
 """
 stack = [] # 创建一个栈
 for brackets in expr: # 迭代传过来的所有字符串
 if brackets in LEFT: # 如果当前字符在左括号内
  stack.append(brackets) # 把当前左括号入栈
 elif brackets in RIGHT: # 如果是右括号
  if not stack or not 1 <= ord(brackets) - ord(stack[-1]) <= 2:
  # 如果当前栈为空，()]
  # 如果右括号减去左括号的值不是小于等于2大于等于1
  return False # 返回False
  stack.pop() # 删除左括号
 return not stack # 如果栈内没有值则返回True，否则返回False
result = match(&#39;[(){()}]&#39;)
print(result)

Problème de labyrinthe

Question

Utilisez un tableau bidimensionnel pour représenter un labyrinthe simple, utilisez 0 pour représenter le passage et 1 pour représenter le bloc. À chaque point, la souris peut se déplacer vers les quatre points adjacents sud-est, nord-ouest et nord-ouest. Concevez un algorithme pour simuler la souris marchant dans le labyrinthe et trouvant un chemin de l'entrée à la sortie.

Comme le montre l'image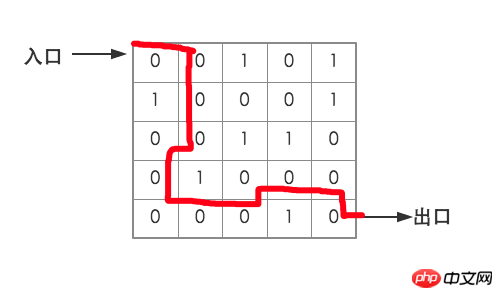

L'itinéraire correct est indiqué par la ligne rouge sur l'image

Réflexion

1. Utilisez une pile pour enregistrer le chemin de la souris de l'entrée à la sortie

2. Après avoir atteint un certain point, poussez le côté gauche du point sur la pile et définissez la valeur du point sur 1, indiquant que vous avez marché

3. Sélectionnez l'un des quatre points à proximité qui peuvent être atteints et marchez jusqu'à ce point ; 🎜>
   Si vous n'allez pas vers les 4 points proches après avoir atteint un certain point, cela signifie que vous êtes dans une impasse. A ce moment, sortez de la pile et prenez du recul pour essayer d'autres points. ;

4. Répétez la deuxième, Trois ou quatre étapes jusqu'à ce que la sortie soit trouvée

5. Résoudre le code

#!/use/bin/env python
# _*_ coding:utf-8 _*_
def initMaze():
 """
 :return: 初始化迷宫
 """
 maze = [[0] * 7 for _ in range(5 + 2)] # 用列表解析创建一个7*7的二维数组，为了确保迷宫四周都是墙
 walls = [ # 记录了墙的位置
 (1, 3),
 (2, 1), (2, 5),
 (3, 3), (3, 4),
 (4, 2), # (4, 3), # 如果把(4, 3)点也设置为墙，那么整个迷宫是走不出去的，所以会返回一个空列表
 (5, 4)
 ]
 for i in range(7): # 把迷宫的四周设置成墙
 maze[i][0] = maze[i][-1] = 1
 maze[0][i] = maze[-1][i] = 1
 for i, j in walls: # 把所有墙的点设置为1
 maze[i][j] = 1
 return maze
"""
[1, 1, 1, 1, 1, 1, 1]
[1, 0, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 1]
[1, 0, 0, 1, 1, 0, 1]
[1, 0, 1, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 1, 1]
"""
def path(maze, start, end):
 """
 :param maze: 迷宫
 :param start: 起始点
 :param end: 结束点
 :return: 行走的每个点
 """
 i, j = start # 分解起始点的坐标
 ei, ej = end # 分解结束点的左边
 stack = [(i, j)] # 创建一个栈，并让老鼠站到起始点的位置
 maze[i][j] = 1 # 走过的路置为1
 while stack: # 栈不为空的时候继续走，否则退出
 i, j = stack[-1] # 获取当前老鼠所站的位置点
 if (i, j) == (ei, ej): break # 如果老鼠找到了出口
 for di, dj in [(0, -1), (0, 1), (-1, 0), (1, 0)]: # 左右上下
  if maze[i + di][j + dj] == 0: # 如果当前点可走
  maze[i + di][j + dj] = 1 # 把当前点置为1
  stack.append((i + di, j + dj)) # 把当前的位置添加到栈里面
  break
 else: # 如果所有的点都不可走
  stack.pop() # 退回上一步
 return stack # 如果迷宫不能走则返回空栈
Maze = initMaze() # 初始化迷宫
result = path(maze=Maze, start=(1, 1), end=(5, 5)) # 老鼠开始走迷宫
print(result)
# [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]

Rechercher l'expression suffixe Valeur

QuestionLors de l'évaluation d'une expression, le compilateur utilise généralement une expression suffixe, qui ne nécessite pas de parenthèses :

编写程序实现后缀表达式求值函数。

思路

1. 建立一个栈来存储待计算的操作数；

2. 遍历字符串，遇到操作数则压入栈中，遇到操作符号则出栈操作数(n次)，进行相应的计算，计算结果是新的操作数压回栈中，等待计算

3. 按上述过程，遍历完整个表达式，栈中只剩下最终结果；
   

解决代码

#!/use/bin/env python
# _*_ coding:utf-8 _*_
operators = { # 运算符操作表
 '+': lambda op1, op2: op1 + op2,
 '-': lambda op1, op2: op1 - op2,
 '*': lambda op1, op2: op1 * op2,
 '/': lambda op1, op2: op1 / op2,
}
def evalPostfix(e):
 """
 :param e: 后缀表达式
 :return: 正常情况下栈内的第一个元素就是计算好之后的值
 """
 tokens = e.split() # 把传过来的后缀表达式切分成列表
 stack = []
 for token in tokens: # 迭代列表中的元素
 if token.isdigit(): # 如果当前元素是数字
  stack.append(int(token)) # 就追加到栈里边
 elif token in operators.keys(): # 如果当前元素是操作符
  f = operators[token] # 获取运算符操作表中对应的lambda表达式
  op2 = stack.pop() # 根据先进后出的原则，先让第二个元素出栈
  op1 = stack.pop() # 在让第一个元素出栈
  stack.append(f(op1, op2)) # 把计算的结果在放入到栈内
 return stack.pop() # 返回栈内的第一个元素
result = evalPostfix('2 3 4 * +')
print(result)
# 14

背包问题

题目

有一个背包能装10kg的物品，现在有6件物品分别为：

物品名称	重量
物品0	1kg
物品1	8kg
物品2	4kg
物品3	3kg
物品4	5kg
物品5	2kg

编写找出所有能将背包装满的解，如物品1+物品5。

解决代码

#!/use/bin/env python
# _*_ coding:utf-8 _*_
def knapsack(t, w):
 """
 :param t: 背包总容量
 :param w: 物品重量列表
 :return:
 """
 n = len(w) # 可选的物品数量
 stack = [] # 创建一个栈
 k = 0 # 当前所选择的物品游标
 while stack or k < n: # 栈不为空或者k<n
 while t > 0 and k < n: # 还有剩余空间并且有物品可装
  if t >= w[k]: # 剩余空间大于等于当前物品重量
  stack.append(k) # 把物品装备背包
  t -= w[k] # 背包空间减少
  k += 1 # 继续向后找
 if t == 0: # 找到了解
  print(stack)
 # 回退过程
 k = stack.pop() # 把最后一个物品拿出来
 t += w[k] # 背包总容量加上w[k]
 k += 1 # 装入下一个物品
knapsack(10, [1, 8, 4, 3, 5, 2])
"""
[0, 2, 3, 5]
[0, 2, 4]
[1, 5]
[3, 4, 5]
"""

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!