Maison >développement back-end >Tutoriel Python >Résolvez le problème des 8 reines en Python sur la base du modèle d'arborescence de sous-ensemble de méthode de retour en arrière
Résolvez le problème des 8 reines en Python sur la base du modèle d'arborescence de sous-ensemble de méthode de retour en arrière
- 巴扎黑original
- 2017-09-02 11:52:421517parcourir
Cet article présente principalement l'implémentation par Python du problème des 8 reines basée sur le modèle d'arbre de sous-ensemble de méthode de backtracking. Il explique brièvement le principe du problème des 8 reines et analyse les techniques d'implémentation spécifiques du modèle d'arbre de sous-ensemble de méthode de backtracking de Python à résoudre. le problème des 8 reines sous forme d'exemples. Les amis dans le besoin peuvent se référer à
Cet article décrit l'exemple de Python implémentant le problème des 8 reines basé sur le modèle d'arborescence de sous-ensemble de méthode de backtracking. Partagez-le avec tout le monde pour votre référence, les détails sont les suivants :
Problème
Placez huit reines sur une grille d'échecs 8×8 afin qu'elles ne puissent pas s'attaquer les unes les autres , c'est-à-dire qu'il n'y a pas deux reines dans la même ligne, colonne ou diagonale. Combien y a-t-il de façons ?

Analyse
Afin de simplifier le problème, considérant que les 8 reines sont dans des rangées différentes, une reine est placée dans chaque ligne, et chaque ligne La reine peut être placée dans les colonnes 0, 1, 2, ..., 7. Nous pensons que la reine dans chaque ligne a 8 états. Ensuite, il suffit d'appliquer le modèle d'arbre de sous-ensemble, en commençant par la ligne 0, de haut en bas, et de parcourir les 8 états de la reine dans chaque ligne.
Code :
'''
8皇后问题
'''
n = 8
x = [] # 一个解(n元数组)
X = [] # 一组解
# 冲突检测:判断 x[k] 是否与前 x[0~k-1] 冲突
def conflict(k):
global x
for i in range(k): # 遍历前 x[0~k-1]
if x[i]==x[k] or abs(x[i]-x[k])==abs(i-k): # 判断是否与 x[k] 冲突
return True
return False
# 套用子集树模板
def queens(k): # 到达第k行
global n, x, X
if k >= n: # 超出最底行
#print(x)
X.append(x[:]) # 保存(一个解),注意x[:]
else:
for i in range(n): # 遍历第 0~n-1 列(即n个状态)
x.append(i) # 皇后置于第i列,入栈
if not conflict(k): # 剪枝
queens(k+1)
x.pop() # 回溯,出栈
# 解的可视化(根据一个解x,复原棋盘。'X'表示皇后)
def show(x):
global n
for i in range(n):
print('. ' * (x[i]) + 'X ' + '. '*(n-x[i]-1))
# 测试
queens(0) # 从第0行开始
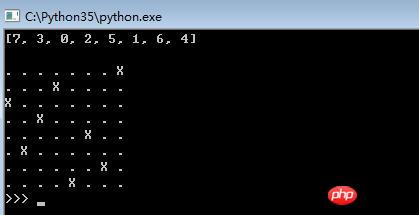
print(X[-1], '\n')
show(X[-1])Rendu
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

