Maison >développement back-end >Tutoriel Python >Explication détaillée de l'utilisation par Python des modèles d'arborescence de sous-ensembles de retour en arrière pour résoudre les problèmes de labyrinthe
Explication détaillée de l'utilisation par Python des modèles d'arborescence de sous-ensembles de retour en arrière pour résoudre les problèmes de labyrinthe
- 巴扎黑original
- 2017-09-02 11:43:462137parcourir
Cet article présente principalement l'utilisation par Python de la méthode de retour en arrière pour résoudre les problèmes de labyrinthe. Il décrit brièvement les principes du problème de labyrinthe et analyse avec des exemples les compétences opérationnelles et les précautions pertinentes pour résoudre le problème de labyrinthe en Python sur la base du sous-ensemble de la méthode de retour en arrière. modèle d'arbre. Obligatoire Les amis peuvent se référer à
Cet article décrit un exemple d'utilisation de la méthode de backtracking pour résoudre des problèmes de labyrinthe en Python. Partagez-le avec tout le monde pour votre référence, les détails sont les suivants :
Problème
Étant donné un labyrinthe, l'entrée est connue. Demandez s'il existe un chemin de l'entrée à la sortie, et si oui, indiquez un tel chemin. Notez que le mouvement peut être effectué dans huit directions : haut, bas, gauche, droite, haut à gauche, haut à droite, bas à gauche et bas à droite. Entrer 0 dans le labyrinthe signifie qu'il peut être parcouru, et entrer 1 signifie qu'il s'agit d'un mur. Pour plus de commodité, entourez le labyrinthe de 1 pour éviter les problèmes de limites.
Analyse
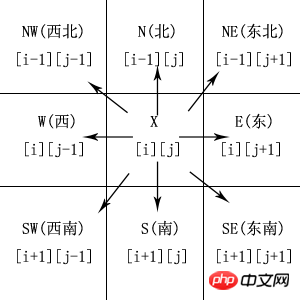
Considérant que gauche et droite sont relatives, elle est modifiée en huit directions : nord, nord-est, est, sud-est, sud, sud-ouest, ouest et nord-ouest. Dans n'importe quelle grille, vous avez le choix entre 8 directions, c'est-à-dire 8 états parmi lesquels choisir. Ainsi, à partir de la grille d’entrée, ces 8 états doivent être traversés à chaque fois que vous entrez dans une grille.
Évidemment, le modèle d'arborescence de sous-ensembles de la méthode de backtracking peut être appliqué.
Notez que la longueur de la solution n'est pas fixe.
Code
# 迷宫(1是墙,0是通路)
maze = [[1,1,1,1,1,1,1,1,1,1],
[0,0,1,0,1,1,1,1,0,1],
[1,1,0,1,0,1,1,0,1,1],
[1,0,1,1,1,0,0,1,1,1],
[1,1,1,0,0,1,1,0,1,1],
[1,1,0,1,1,1,1,1,0,1],
[1,0,1,0,0,1,1,1,1,0],
[1,1,1,1,1,0,1,1,1,1]]
m, n = 8, 10 # 8行,10列
entry = (1,0) # 迷宫入口
path = [entry] # 一个解(路径)
paths = [] # 一组解
# 移动的方向(顺时针8个:N, EN, E, ES, S, WS, W, WN)
directions = [(-1,0),(-1,1),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1)]
# 冲突检测
def conflict(nx, ny):
global m,n,maze
# 是否在迷宫中,以及是否可通行
if 0 <= nx < m and 0 <= ny < n and maze[nx][ny]==0:
return False
return True
# 套用子集树模板
def walk(x, y): # 到达(x,y)格子
global entry,m,n,maze,path,paths,directions
if (x,y) != entry and (x % (m-1) ==0 or y % (n-1) == 0): # 出口
#print(path)
paths.append(path[:]) # 直接保存,未做最优化
else:
for d in directions: # 遍历8个方向(亦即8个状态)
nx, ny = x+d[0], y+d[1]
path.append((nx,ny)) # 保存,新坐标入栈
if not conflict(nx, ny): # 剪枝
maze[nx][ny] = 2 # 标记,已访问(奇怪,此两句只能放在if区块内!)
walk(nx, ny)
maze[nx][ny] = 0 # 回溯,恢复
path.pop() # 回溯,出栈
# 解的可视化(根据一个解x,复原迷宫路径,'2'表示通路)
def show(path):
global maze
import pprint, copy
maze2 = copy.deepcopy(maze)
for p in path:
maze2[p[0]][p[1]] = 2 # 通路
pprint.pprint(maze) # 原迷宫
print()
pprint.pprint(maze2) # 带通路的迷宫
# 测试
walk(1,0)
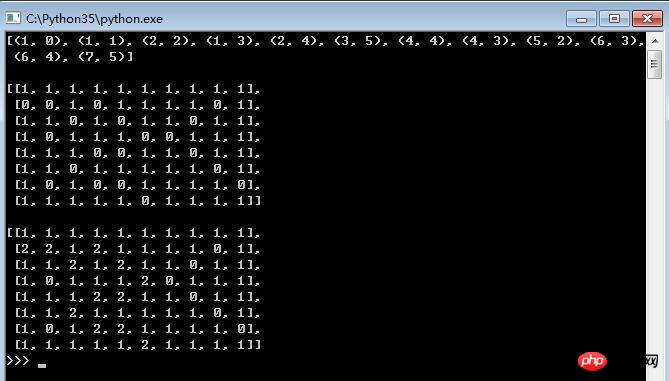
print(paths[-1], '\n') # 看看最后一条路径
show(paths[-1])Rendu
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

