Résumé et exemples de l'algorithme de tri Python

Cet article présente principalement les informations pertinentes sur le résumé de l'algorithme de tri Python et des exemples détaillés. Les amis qui en ont besoin peuvent s'y référer

Il résume les algorithmes de tri centralisés courants

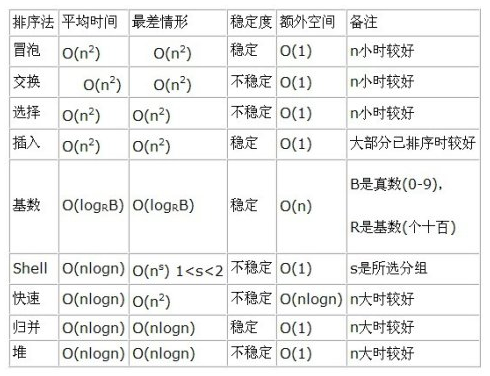
Tri par fusion

Le tri par fusion, également appelé tri par fusion, est une application typique de la méthode diviser pour régner. L'idée de diviser pour régner est de décomposer chaque problème en petits problèmes, de résoudre chaque petit problème, puis de les fusionner.

Le tri par fusion spécifique consiste à décomposer récursivement un ensemble de nombres non ordonnés en sous-éléments avec un seul élément par n/2, et un élément est déjà trié. Fusionnez ensuite ces sous-éléments ordonnés.

Le processus de fusion consiste à comparer deux sous-séquences triées, à sélectionner d'abord le plus petit élément des deux sous-séquences, à sélectionner la plus petite sous-séquence des deux éléments et à la supprimer de la sous-séquence

Supprimer et ajouter au jeu de résultats final jusqu'à ce que les deux sous-séquences soient fusionnées.

Le code est le suivant :

#!/usr/bin/python 
import sys 
 
def merge(nums, first, middle, last): 
  ''''' merge ''' 
  # 切片边界,左闭右开并且是了0为开始 
  lnums = nums[first:middle+1] 
  rnums = nums[middle+1:last+1] 
  lnums.append(sys.maxint) 
  rnums.append(sys.maxint) 
  l = 0 
  r = 0 
  for i in range(first, last+1): 
    if lnums[l] < rnums[r]: 
      nums[i] = lnums[l] 
      l+=1 
    else: 
      nums[i] = rnums[r] 
      r+=1 
def merge_sort(nums, first, last): 
  &#39;&#39;&#39;&#39;&#39; merge sort
  merge_sort函数中传递的是下标，不是元素个数
  &#39;&#39;&#39; 
  if first < last: 
    middle = (first + last)/2 
    merge_sort(nums, first, middle) 
    merge_sort(nums, middle+1, last) 
    merge(nums, first, middle,last) 
 
if __name__ == &#39;__main__&#39;: 
  nums = [10,8,4,-1,2,6,7,3] 
  print &#39;nums is:&#39;, nums 
  merge_sort(nums, 0, 7) 
  print &#39;merge sort:&#39;, nums

Stable, complexité temporelle O(nlog n)

Insertion Le code de tri

est le suivant :

#!/usr/bin/python 
importsys 
 
definsert_sort(a): 
  ''''' 插入排序
  有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，
  但要求插入后此数据序列仍然有序。刚开始 一个元素显然有序，然后插入一
  个元素到适当位置，然后再插入第三个元素，依次类推
  ''' 
  a_len = len(a) 
  if a_len = 0 and a[j] > key: 
      a[j+1] = a[j] 
      j-=1 
    a[j+1] = key 
  return a 
 
if __name__ == '__main__': 
  nums = [10,8,4,-1,2,6,7,3] 
  print 'nums is:', nums 
  insert_sort(nums) 
  print 'insert sort:', nums

est stable et la complexité temporelle est O(n^2)

Pour échanger les valeurs de deux éléments, vous pouvez écrire ceci en python : a, b = b, a En fait, c'est parce que les côtés gauche et droit du. Les symboles d'affectation sont des tuples

(ce qu'il faut souligner ici, c'est qu'en python, les tuples sont en fait délimités par des virgules "," au lieu de crochets).

Tri par sélection

Le tri par sélection est un algorithme de tri simple et intuitif. Voici comment cela fonctionne. Tout d'abord, trouvez le plus petit (grand) élément de la séquence non triée et stockez-le à la position de départ de la séquence triée

Ensuite, continuez à trouver le plus petit (grand) élément parmi les éléments non triés restants, et. puis placez-le dans la séquence triée en fin de séquence. Et ainsi de suite, jusqu'à ce que tous les éléments

soient triés.

import sys 
def select_sort(a): 
  ''''' 选择排序 
  每一趟从待排序的数据元素中选出最小（或最大）的一个元素，
  顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。
  选择排序是不稳定的排序方法。
  ''' 
  a_len=len(a) 
  for i in range(a_len):#在0-n-1上依次选择相应大小的元素 
    min_index = i#记录最小元素的下标 
    for j in range(i+1, a_len):#查找最小值 
      if(a[j]<a[min_index]): 
        min_index=j 
    if min_index != i:#找到最小元素进行交换 
      a[i],a[min_index] = a[min_index],a[i] 
 
if __name__ == &#39;__main__&#39;: 
  A = [10, -3, 5, 7, 1, 3, 7]  
  print &#39;Before sort:&#39;,A  
  select_sort(A)  
  print &#39;After sort:&#39;,A

Instable, complexité temporelle O(n^2)

Tri par colline

Tri Hill, également connu sous le nom d'algorithme de tri incrémentiel descendant, le tri Hill est un algorithme de tri non stable. Cette méthode est également appelée réduction du tri incrémentiel, car DL. Shell doit son nom à sa proposition en 1959.

Prenez d'abord un entier d1 inférieur à n comme premier incrément et divisez tous les enregistrements du fichier en groupes d1. Tous les enregistrements dont la distance est un multiple de d1 sont placés dans le même groupe. Triez d'abord au sein de chaque groupe

Ensuite, prenez le deuxième incrément d2

import sys 
def shell_sort(a): 
  ''''' shell排序 
  ''' 
  a_len=len(a) 
  gap=a_len/2#增量 
  while gap>0: 
    for i in range(a_len):#对同一个组进行选择排序 
      m=i 
      j=i+1 
      while j<a_len: 
        if a[j]<a[m]: 
          m=j 
        j+=gap#j增加gap 
      if m!=i: 
        a[m],a[i]=a[i],a[m] 
    gap/=2 
 
if __name__ == &#39;__main__&#39;: 
  A = [10, -3, 5, 7, 1, 3, 7]  
  print &#39;Before sort:&#39;,A  
  shell_sort(A)  
  print &#39;After sort:&#39;,A

Instable, complexité temporelle Temps moyen O(nlogn) Pire moment O(n^s)1

Heap Sort (Heap Sort)

La définition de "heap": dans Dans le "heap" avec un indice de départ de 0 :

Le nœud enfant droit du nœud i est à la position 2 * i 24) Le nœud parent du nœud i est à la position floor( (i – 1) / 2) : Note floor Représente l'opération "arrondi"

Caractéristiques du tas :

La valeur clé de chaque nœud doit toujours être supérieure (ou inférieure) à son nœud parent

"Maximum Heap " :

Le nœud racine du "heap" enregistre le nœud avec la plus grande valeur de clé. Autrement dit, la valeur clé de chaque nœud du « tas » est toujours supérieure à celle de ses nœuds enfants.

Monter, descendre :

Lorsque la valeur clé d'un nœud est supérieure à son nœud parent, alors nous devons effectuer une opération de "monter", c'est-à-dire que nous déplaçons le nœud à La position de son nœud parent, et laissons son nœud parent aller à sa position, puis nous continuons à juger le nœud, et n'arrêtons pas de "monter" jusqu'à ce que le nœud ne soit plus plus grand que son nœud parent.

Jetons maintenant un coup d'œil à l'opération « descendre ». Lorsque nous modifions la valeur clé d'un nœud en une valeur plus petite, nous devons le "déplacer vers le bas".

Méthode :

On construit d'abord un tas maximum (complexité temporelle O(n)), puis à chaque fois il suffit d'échanger le nœud racine avec le nœud en dernière position, et puis mettez la dernière position. Une position est exclue, puis le tas du nœud racine est ajusté après l'échange (complexité temporelle O(lgn)), c'est-à-dire que le nœud racine est "déplacé vers le bas". La complexité temporelle totale du tri par tas est O(nlgn).

Le code est le suivant :

#!/usr/bin env python 
 
# 数组编号从 0开始 
def left(i): 
  return 2*i +1 
def right(i): 
  return 2*i+2 
 
#保持最大堆性质 使以i为根的子树成为最大堆 
def max_heapify(A, i, heap_size): 
  if heap_size <= 0: 
    return 
  l = left(i) 
  r = right(i) 
  largest = i # 选出子节点中较大的节点 
  if l A[largest]: 
    largest = l 
  if r A[largest]: 
    largest = r 
  if i != largest :#说明当前节点不是最大的，下移 
    A[i], A[largest] = A[largest], A[i] #交换 
    max_heapify(A, largest, heap_size)#继续追踪下移的点 
  #print A 
# 建堆  
def bulid_max_heap(A): 
  heap_size = len(A) 
  if heap_size >1: 
    node = heap_size/2 -1 
    while node >= 0: 
     max_heapify(A, node, heap_size) 
     node -=1 
 
# 堆排序 下标从0开始 
def heap_sort(A): 
  bulid_max_heap(A) 
  heap_size = len(A) 
  i = heap_size - 1 
  while i > 0 : 
    A[0],A[i] = A[i], A[0] # 堆中的最大值存入数组适当的位置，并且进行交换 
    heap_size -=1 # heap 大小 递减 1 
    i -= 1 # 存放堆中最大值的下标递减 1 
    max_heapify(A, 0, heap_size) 
 
if __name__ == &#39;__main__&#39; : 
 
  A = [10, -3, 5, 7, 1, 3, 7] 
  print &#39;Before sort:&#39;,A 
  heap_sort(A) 
  print &#39;After sort:&#39;,A

Instable, complexité temporelle O(nlog n)

Tri rapide

L'algorithme de tri rapide, comme l'algorithme de tri par fusion, est également basé sur le mode diviser pour régner. Les trois étapes du processus diviser pour régner de tri rapide du sous-tableau A[p…r] sont :

Décomposition : diviser le tableau A[p…r] en A[p…q-1] et A[ q 1...r] deux parties, où chaque élément de A[p...q-1] est inférieur ou égal à A[q] et chaque élément de A[q 1...r] est supérieur ou égal à A[q];

Solution : Triez les sous-tableaux A[p...q-1] et A[q 1...r] en appelant de manière récursive le tri rapide

Fusionner : étant donné que les deux sous-tableaux sont triés, aucune opération supplémentaire n'est requise.

Pour le début de chaque itération de partition, x=A[r], pour tout indice de tableau k, il y a :

1) Si p≤k≤i, alors A[ k]≤x.

2) Si i 1≤k≤j-1, alors A[k]>x.

3) Si k=r, alors A[k]=x.

Le code est le suivant :

#!/usr/bin/env python 
# 快速排序 
'''''
划分 使满足 以A[r]为基准对数组进行一个划分，比A[r]小的放在左边，
  比A[r]大的放在右边
快速排序的分治partition过程有两种方法，
一种是上面所述的两个指针索引一前一后逐步向后扫描的方法,
另一种方法是两个指针从首位向中间扫描的方法。
''' 
#p,r 是数组A的下标 
def partition1(A, p ,r): 
  '''''
   方法一，两个指针索引一前一后逐步向后扫描的方法
  ''' 
  x = A[r] 
  i = p-1 
  j = p 
  while j < r: 
    if A[j] < x: 
      i +=1 
      A[i], A[j] = A[j], A[i] 
    j += 1 
  A[i+1], A[r] = A[r], A[i+1] 
  return i+1 
 
def partition2(A, p, r): 
  &#39;&#39;&#39;&#39;&#39;
  两个指针从首尾向中间扫描的方法
  &#39;&#39;&#39; 
  i = p 
  j = r 
  x = A[p] 
  while i = x and i < j: 
      j -=1 
    A[i] = A[j] 
    while A[i]<=x and i < j: 
      i +=1 
    A[j] = A[i] 
  A[i] = x 
  return i 
 
# quick sort 
def quick_sort(A, p, r): 
  &#39;&#39;&#39;&#39;&#39;
    快速排序的最差时间复杂度为O(n2)，平时时间复杂度为O(nlgn)
  &#39;&#39;&#39; 
  if p < r: 
    q = partition2(A, p, r) 
    quick_sort(A, p, q-1) 
    quick_sort(A, q+1, r) 
 
if __name__ == &#39;__main__&#39;: 
 
  A = [5,-4,6,3,7,11,1,2] 
  print &#39;Before sort:&#39;,A 
  quick_sort(A, 0, 7) 
  print &#39;After sort:&#39;,A

Instable, la meilleure complexité temporelle est O(nlogn) et le pire moment est O(n^2)

Parlons des séquences en python :

Listes, tuples et chaînes C'est toutes les séquences, mais que sont les séquences et pourquoi sont-elles si spéciales ? Les deux principales caractéristiques des séquences sont l’opérateur d’indexation et l’opérateur de découpage. L'opérateur d'index nous permet de récupérer un élément spécifique d'une séquence. L'opérateur slice permet d'obtenir une tranche de la séquence, c'est-à-dire une partie de la séquence, telle que : a = ['aa','bb','cc'], print a[0] est une opération d'index , imprimez a[0:2] pour les opérations de découpage.

J'espère maîtriser la connaissance du tri des algorithmes Python à travers cet article Merci pour votre soutien à ce site !

Pour plus d'articles liés au résumé et aux exemples de l'algorithme de tri Python, veuillez faire attention au site Web PHP chinois !