Tsinghua Optics AI apparaît dans Nature ! Réseau neuronal physique, la rétropropagation n'est plus nécessaire

Utiliser la lumière pour entraîner les réseaux de neurones, les résultats de l’Université Tsinghua ont été récemment publiés dans Nature !

Que dois-je faire si l'algorithme de rétropropagation ne peut pas être appliqué ?

Ils ont proposé une méthode de formation en mode entièrement avancé (FFM), qui effectue directement le processus de formation dans le système optique physique, surmontant ainsi les limites des simulations informatiques numériques traditionnelles.

Pour faire simple, il fallait autrefois modéliser le système physique en détail puis simuler ces modèles sur ordinateur pour entraîner le réseau. La méthode FFM élimine le processus de modélisation et permet au système d'utiliser directement les données expérimentales pour l'apprentissage et l'optimisation.

Cela signifie également que la formation n'a plus besoin de vérifier chaque couche d'arrière en avant (rétropropagation), mais peut directement mettre à jour les paramètres du réseau d'avant en arrière.

Par exemple, tout comme un puzzle, la rétropropagation doit d'abord voir l'image finale (sortie), puis la vérifier et la restaurer pièce par pièce à l'envers, tandis que la méthode FFM ressemble plus à un puzzle partiellement terminé en main, et seulement ; doit suivre quelques principes légers (réciprocité symétrique) Continuez à remplir sans revenir en arrière pour vérifier les pièces du puzzle précédentes.

De cette façon, les avantages de l'utilisation de FFM sont également évidents :

Premièrement, cela réduit la dépendance aux modèles mathématiques, ce qui peut éviter les problèmes causés par des modèles inexacts. Deuxièmement, cela permet de gagner du temps (et consomme moins d'énergie) ; L'utilisation de systèmes optiques permet de traiter en parallèle de grandes quantités de données et d'opérations, et l'élimination de la rétropropagation réduit également le nombre d'étapes à travers le réseau qui doivent être vérifiées et ajustées.

Les co-auteurs de l'article sont Xue Zhiwei et Zhou Tiankui de l'Université Tsinghua, et les auteurs correspondants sont le professeur Fang Lu et l'académicien Dai Qionghai de l'Université Tsinghua. De plus, Xu Zhihao du Département d'électronique de l'Université Tsinghua et Yu Shaoliang du laboratoire Zhijiang ont également participé à cette recherche.

Éliminer la rétropropagation

Résumé du principe FFM en une phrase :

Mappez le système optique dans un réseau neuronal paramétré sur site, calculez le gradient en mesurant le champ lumineux de sortie et mettez à jour les paramètres à l'aide de l'algorithme de descente de gradient.

En termes simples, cela signifie laisser le système optique s'auto-apprendre, comprendre ses propres performances en observant comment il traite la lumière (c'est-à-dire en mesurant le champ lumineux de sortie), puis utiliser ces informations pour ajuster progressivement ses réglages (paramètres).

La figure suivante montre le mécanisme de fonctionnement du FFM dans un système optique :

où a est la limitation de la méthode de conception traditionnelle ; b est la composition du système optique ; c est la cartographie du système optique avec le réseau neuronal ; .

En expansion, le système optique général (b), comprenant l'optique de lentille en espace libre et la photonique intégrée, se compose d'une région de modulation (vert foncé) et d'une région de propagation (vert clair). Dans ces régions, l'indice de réfraction de la région de modulation est réglable, tandis que l'indice de réfraction de la région de propagation est fixe.

Et les zones de modulation et de propagation ici peuvent être mappées aux poids et aux connexions neuronales du réseau neuronal.

Dans un réseau neuronal, ces parties réglables sont comme des points de connexion entre les neurones et peuvent changer leur force (poids) pour apprendre.

En utilisant le principe de réciprocité de symétrie spatiale, les données et le calcul des erreurs peuvent partager le même processus de propagation physique vers l'avant et la même méthode de mesure.

C'est un peu comme un reflet dans un miroir, chaque partie du système répond de la même manière à la propagation de la lumière et aux retours d'erreur. Cela signifie que quelle que soit la manière dont la lumière pénètre dans le système, celui-ci la traite de manière cohérente et s'ajuste en fonction des résultats.

De cette manière, le gradient peut être calculé directement sur site et utilisé pour mettre à jour l'indice de réfraction dans la zone de conception, optimisant ainsi les performances du système.

Grâce à la méthode de descente de gradient sur site, le système optique peut ajuster progressivement ses paramètres jusqu'à ce qu'il atteigne l'état optimal.

Le texte original utilise l'équation pour finalement exprimer la méthode de descente de gradient en mode avant complet mentionnée ci-dessus (remplaçant la rétropropagation) comme :

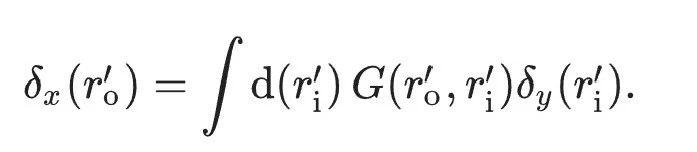
Une méthode de formation de réseau de neurones optiques

En tant que méthode de formation de réseau de neurones optiques, FFM It présente les avantages suivants :

Précision comparable au modèle idéal

L'utilisation de FFM peut réaliser un processus d'auto-formation efficace sur le réseau neuronal optique en espace libre (Optical Neural Network, ONN).

Pour illustrer cette conclusion, les chercheurs ont d'abord utilisé un ONN monocouche pour effectuer un entraînement à la classification d'objets sur l'ensemble de données de référence (a).

Plus précisément, ils ont utilisé quelques images de chiffres manuscrits (ensemble de données MNIST) pour entraîner ce système, puis ont visualisé les résultats (b).

Les résultats montrent que l'ONN formé par l'apprentissage FFM présente une similitude extrêmement élevée entre le champ lumineux expérimental et le champ lumineux théorique (SSIM dépasse 0,97).

En d’autres termes, il apprend si bien qu’il peut presque parfaitement copier les exemples qui lui sont donnés.

Cependant, les chercheurs rappellent également :

En raison des imperfections du système, les champs lumineux et les gradients théoriquement calculés ne peuvent pas refléter avec précision les phénomènes physiques réels.

Ensuite, les chercheurs ont utilisé des images plus complexes (ensemble de données Fashion-MNIST) pour entraîner le système à reconnaître différents articles de mode.

Au début, lorsque le nombre de couches passait de 2 à 8, la précision moyenne du réseau formé par ordinateur était presque la moitié de la précision théorique.

Grâce à la méthode d'apprentissage FFM, la précision du réseau du système a été augmentée à 92,5%, ce qui est proche de la valeur théorique.

Cela montre qu'à mesure que le nombre de couches réseau augmente, les performances du réseau formé par les méthodes traditionnelles diminuent, tandis que l'apprentissage FFM peut maintenir une grande précision.

Dans le même temps, les performances d'ONN peuvent être encore améliorées en intégrant l'activation non linéaire dans l'apprentissage FFM. Lors d'expériences, l'apprentissage FFM non linéaire a permis d'améliorer la précision de la classification de 90,4 % à 93,0 %.

La recherche prouve en outre qu'en entraînant des ONN non linéaires par lots, le processus de propagation des erreurs peut être simplifié et le temps d'entraînement n'augmente que de 1 à 1,7 fois.

Capacité de mise au point haute résolution

FFM peut également obtenir une imagerie de haute qualité dans des applications pratiques, atteignant une résolution proche de la limite physique, même dans des environnements de diffusion complexes.

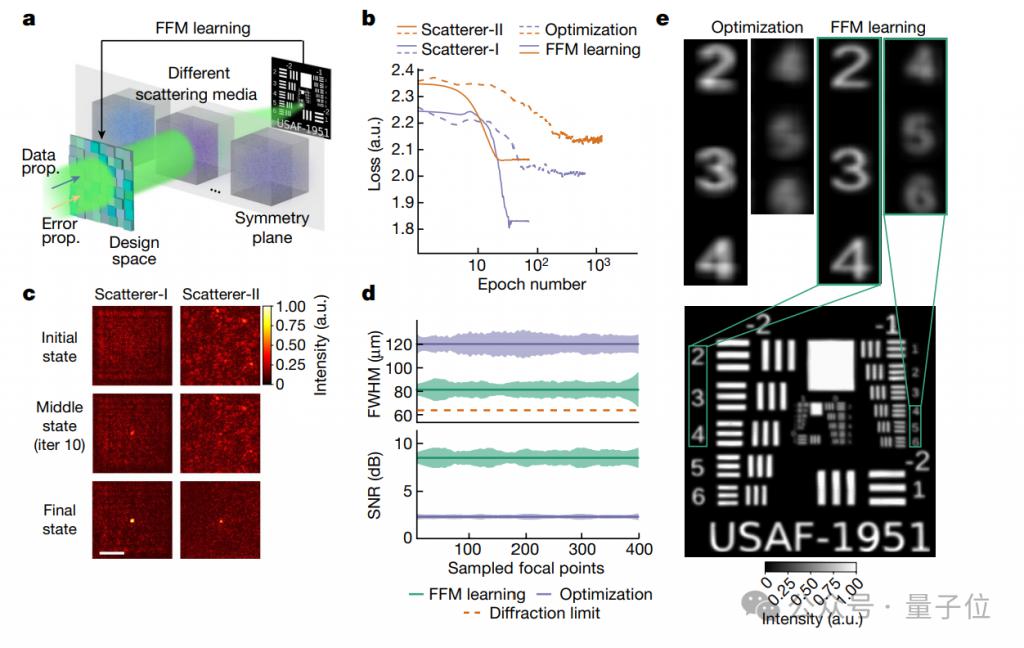
Tout d'abord, lorsque les ondes lumineuses pénètrent dans un milieu diffusant (comme le brouillard, la fumée ou les tissus biologiques, etc.), la focalisation va devenir compliquée, mais la propagation des ondes lumineuses dans le milieu conserve souvent une certaine symétrie.

FFM profite de cette symétrie en optimisant le chemin de propagation et la phase des ondes lumineuses pour réduire l'impact négatif des effets de diffusion sur la focalisation.

L'effet est également très significatif. La figure b montre la comparaison des deux méthodes d'optimisation, FFM et PSO (Particle Swarm Optimization).

Plus précisément, l'expérience a utilisé deux supports de diffusion, l'un est une plaque à phase aléatoire (Scatterer-I) et l'autre est un ruban transparent (Scatterer-II).

Dans les deux médias, FFM a atteint la convergence (trouver plus rapidement la solution optimale) après seulement 25 itérations de conception, avec des valeurs de perte de convergence de 1,84 et 2,07 respectivement (plus les performances sont faibles).

La méthode PSO nécessite au moins 400 itérations de conception pour atteindre la convergence, et les valeurs de perte à la convergence finale sont de 2,01 et 2,15.

Dans le même temps, la figure c montre que FFM est capable de s'optimiser en permanence et que son orientation est conçue pour évoluer progressivement et converger d'une distribution aléatoire initiale vers une orientation étroite.

Dans une zone de conception de 3,2 mm × 3,2 mm, les chercheurs ont en outre échantillonné uniformément les foyers optimisés FFM et PSO et comparé leur FWHM (pleine largeur à mi-hauteur) et PSNR (rapport signal/bruit de pointe).

Les résultats montrent que FFM a une précision de mise au point plus élevée et une meilleure qualité d'imagerie.

La figure e évalue en outre les performances du réseau de focalisation conçu lors de la numérisation d'une carte de résolution située derrière un milieu de diffusion.

Les résultats sont surprenants. La taille du foyer de la conception FFM est proche de la limite de diffraction de 64,5 m, qui est la norme théorique de résolution la plus élevée pour l'imagerie optique.

Capable d'imager en parallèle des objets en dehors de la ligne de mire

Comme il est si puissant dans les médias de diffusion, les chercheurs ont également essayé des scénarios sans ligne de mire (NLOS), dans lesquels les objets sont cachés à la vue.

FFM exploite la symétrie spatiale du trajet lumineux de l'objet caché à l'observateur, ce qui permet au système de reconstruire et d'analyser les objets cachés dynamiques sur le terrain de manière entièrement optique.

En concevant le front d'onde d'entrée, FFM est capable de projeter simultanément tous les maillages de l'objet vers leurs positions cibles, réalisant ainsi une récupération parallèle des objets cachés.

Les cibles de chrome cachées en forme de lettre "T", "H" et "U" ont été utilisées dans l'expérience, et le temps d'exposition (1 milliseconde) et la puissance optique (0,20 mW) ont été réglés pour obtenir une imagerie rapide de ces dynamiques. cibles.

Les résultats montrent que sans le front d'onde conçu par FFM, l'image sera gravement déformée. Alors que le front d'onde conçu par FFM a pu récupérer les formes des trois lettres, le SSIM (indice de similarité structurelle) a atteint 1,0, indiquant un degré élevé de similitude avec l'image originale.

De plus, comparé au réseau neuronal artificiel (ANN) en termes d'efficacité des photons et de performances de classification, le FFM surpasse considérablement l'ANN, en particulier dans des conditions de faibles photons.

Plus précisément, dans les situations où le nombre de photons est limité (comme de nombreuses surfaces réfléchissantes ou très diffuses), FFM est capable de corriger de manière adaptative la distorsion du front d'onde et nécessite moins de photons pour une classification précise.

Recherche automatique de valeurs aberrantes dans les systèmes non hermitiens

La méthode FFM convient non seulement aux systèmes optiques en espace libre, mais peut également être étendue à l'auto-conception de systèmes photoniques intégrés.

Les chercheurs ont construit un réseau neuronal intégré (a) utilisant des noyaux photoniques symétriques configurés en série et en parallèle.

Dans l'expérience, le noyau symétrique a été configuré avec un atténuateur optique variable (VOA) via différents niveaux de courant d'injection pour obtenir différents coefficients d'atténuation afin de simuler différents poids.

Dalam Rajah c, ketepatan nilai matriks yang diprogramkan dalam teras simetri adalah sangat tinggi, dengan sisihan piawai hanyut masa masing-masing 0.012%, 0.012% dan 0.010%, menunjukkan bahawa nilai matriks sangat stabil.

Dan, para penyelidik memvisualisasikan ralat untuk setiap lapisan. Membandingkan kecerunan eksperimen dengan nilai simulasi teori, sisihan purata ialah 3.5%.

Selepas kira-kira 100 lelaran (zaman), rangkaian mencapai penumpuan.

Hasil eksperimen menunjukkan bahawa di bawah tiga konfigurasi nisbah simetri yang berbeza (1.0, 0.75 atau 0.5), ketepatan pengelasan rangkaian ialah 94.7%, 89.2% dan 89.0% masing-masing.

Ketepatan klasifikasi yang diperoleh dengan menggunakan rangkaian neural menggunakan kaedah FFM ialah 94.2%, 89.2% dan 88.7%.

Sebaliknya, jika kaedah simulasi komputer tradisional digunakan untuk mereka bentuk rangkaian, ketepatan pengelasan eksperimen akan menjadi lebih rendah, masing-masing 71.7%, 65.8% dan 55.0%.

Akhirnya, para penyelidik juga menunjukkan bahawa FFM boleh mereka bentuk sendiri sistem bukan Hermitian dan mencapai lintasan titik tunggal tanpa memerlukan model fizikal melalui simulasi berangka.

Sistem bukan Hermitian ialah konsep dalam fizik, yang melibatkan sistem dalam bidang seperti mekanik kuantum dan optik, yang tidak memenuhi syarat Hermitian.

Sifat Hermitian adalah berkaitan dengan simetri sistem dan bilangan sebenar sistem bukan Hermitian Mereka mungkin mempunyai beberapa fenomena fizikal yang istimewa, seperti titik luar biasa (Exceptional Points), yang merupakan dinamik. di mana tingkah laku pembelajaran mengalami perubahan aneh pada titik tertentu.

Untuk meringkaskan artikel penuh, FFM ialah kaedah untuk melaksanakan proses latihan intensif secara pengiraan pada sistem fizikal, yang mampu melaksanakan kebanyakan operasi pembelajaran mesin secara selari dengan cekap.

Untuk tetapan percubaan yang lebih terperinci dan proses penyediaan set data, sila rujuk artikel asal.

Kod:

https://zenodo.org/records/10820584

Teks asal "Nature":

https://www.nature.com/articles/s41586-024-07687-4

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!