JavaScript Data Structures and Algorithms Graphs and Graph Algorithms_Basic Knowledge

Definition of graph

Graph is composed of a finite non-empty set of vertices and a set of edges between vertices. It is usually expressed as: G(V,E), where G represents a graph and V is the vertex of the graph G. Set, E is the set of edges in graph G.

Directed graph

Directed edge: If the edge from vertex Vi to Vj has a direction, then this edge is called a directed edge, also called an arc (Arc), represented by an ordered pair , Vi is called is the arc tail, and Vj is called the arc head.

Unordered graph

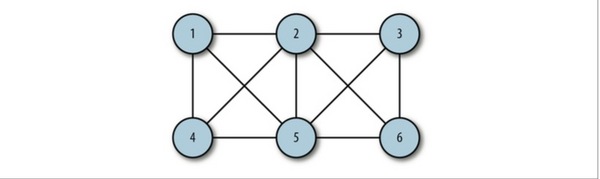
Undirected edge: If the edge between vertices Vi and Vj has no direction, this edge is called an undirected edge (Edge) and is represented by an unordered pair (Vi, Vj).

Simple picture

Simple graph: In the graph structure, if there is no edge from a vertex to itself, and the same edge does not appear repeatedly, then such a graph is called a simple graph.

Graphics

represents the vertex

The first step in creating a graph class is to create a Vertex class to save vertices and edges. The function of this class is the same as the Node class of linked list and binary search tree. The Vertex class has two data members: one that identifies the vertex, and a Boolean value that indicates whether it has been visited. They are named label and wasVisited respectively.

Copy code The code is as follows:

function Vertex(label){
This.label = label;
}

We save all the vertices in an array, and in the graph class, they can be referenced by their position in the array

represents an edge

The actual information of the graph is stored on the "edges" because they describe the structure of the graph. A parent node of a binary tree can only have two child nodes, but the structure of the graph is much more flexible. A vertex can have one edge or multiple edges connected to it.

We call the method of representing the edges of a graph an adjacency list or an adjacency list array. It will store an array consisting of a list of adjacent vertices of a vertex

Construction diagram

Define a Graph class as follows:

Copy code The code is as follows:

function Graph(v){
This.vertices = v;//vertices highest point
This.edges = 0;
This.adj = [];
for(var i =0;I This.adj[i] = [];
This.adj[i].push('');
}
This.addEdge = addEdge;
This.toString = toString;
}

This class records how many edges a graph represents and records the number of vertices using a length and the number of vertices in the graph.

Copy code The code is as follows:

function addEdge(){
This.adj[v].push(w);
This.adj[w].push(v);
This.edges ;
}

Here we use a for loop to add a sub-array to each element in the array to store all adjacent vertices, and initialize all elements to empty strings.

Graph traversal

Depth-first traversal

DepthFirstSearch, also known as depth-first search, referred to as DFS.

For example, if you are looking for a key in a room, you can start from any room. Search the corners, bedside tables, beds, under the beds, wardrobes, TV cabinets, etc. in the room one by one, so as not to miss any one. Dead end, after searching all the drawers and storage cabinets, then look for the next room.

Depth first search:

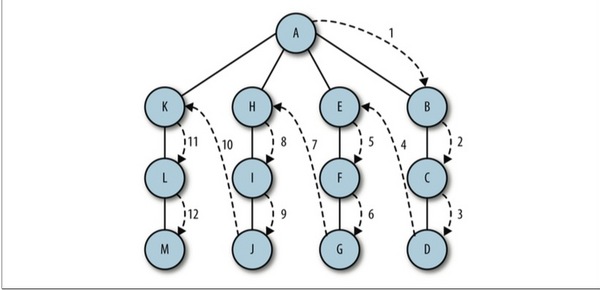
Depth-first search is to visit an unvisited vertex, mark it as visited, and then recursively access other unvisited vertices in the adjacency list of the initial vertex

Add an array to the Graph class:

Copy code The code is as follows:

this.marked = [];//Save the visited vertices
for(var i=0;i This.marked[i] = false;//Initialized to false
}

Depth-first search function:

Copy code The code is as follows:

function dfs(v){
This.marked[v] = true;
//The if statement is not necessary here
If(this.adj[v] != undefined){
​​​​print("Visited vertex: " v );
for each(var w in this.adj[v]){
If(!this.marked[w]){
This.dfs(w);
            }
}
}
}

Breadth-first search

Breadth-first search (BFS) is a blind search method that aims to systematically expand and examine all nodes in the graph to find results. In other words, it does not consider the possible locations of the results and searches the entire graph thoroughly until the results are found.

Breadth-first search starts from the first vertex and tries to visit vertices as close to it as possible, as shown below:

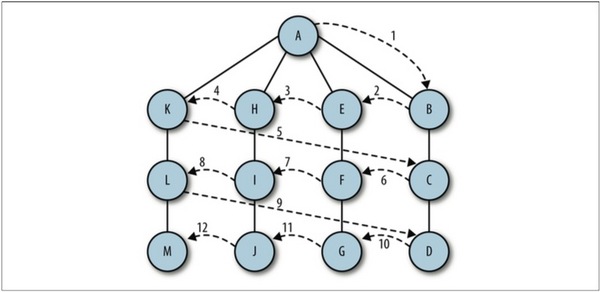
Its working principle is:

1. First find the unvisited vertices adjacent to the current vertex and add them to the visited vertex list and queue;
2. Then take the next vertex v from the graph and add it to the visited vertex list
3. Finally, add all unvisited vertices adjacent to v to the queue
The following is the definition of the breadth-first search function:

Copy code The code is as follows:

function bfs(s){
var queue = [];
This.marked = true;
Queue.push(s);//Add to the end of the queue
While(queue.length>0){
          var v = queue.shift();//Remove from the head of the queue
If(v == undefined){
                                      print("Visited vertex: " v);
}
for each(var w in this.adj[v]){
If(!this.marked[w]){
This.edgeTo[w] = v;
This.marked[w] = true;
queue.push(w);
            }
}
}
}

Shortest path

When performing a breadth-first search, the shortest path from one vertex to another connected vertex is automatically found

Determine the path

To find the shortest path, you need to modify the breadth-first search algorithm to record the path from one vertex to another vertex. We need an array to save all the edges from one vertex to the next vertex. We name this array edgeTo

Copy code The code is as follows:

this.edgeTo = [];//Add this line to the Graph class

//bfs function
function bfs(s){
var queue = [];
This.marked = true;
Queue.push(s);//Add to the end of the queue
While(queue.length>0){
          var v = queue.shift();//Remove from the head of the queue
If(v == undefined){
                                      print("Visited vertex: " v);
}
for each(var w in this.adj[v]){
If(!this.marked[w]){
This.edgeTo[w] = v;
This.marked[w] = true;
queue.push(w);
            }
}
}
}

Topological sorting algorithm

Topological sorting will sort all the vertices of the directed graph so that the directed edges point from the previous vertices to the later vertices.
The topological sorting algorithm is similar to BFS. The difference is that the topological sorting algorithm does not immediately output the visited vertices. Instead, it visits all adjacent vertices in the adjacency list of the current vertex. The current vertex will not be pushed in until the list is exhausted. in the stack.

The topological sorting algorithm is split into two functions. The first function is topSort(), which is used to set up the sorting process and call an auxiliary function topSortHelper(), and then display the sorted vertex list

The main work of the topological sorting algorithm is completed in the recursive function topSortHelper(). This function will mark the current vertex as visited, and then recursively access each vertex in the current vertex adjacency list to mark these vertices as visited. Finally, the current vertex is pushed onto the stack.

Copy code The code is as follows:

//topSort() function
function topSort(){
var stack = [];
var visited = [];
for(var i =0;i         visited[i] = false;
}
for(var i = 0;i If(visited[i] == false){
This.topSortHelper(i,visited,stack);
}
}
for(var i = 0;i If(stack[i] !=undefined && stack[i] != false){
                   print(this.vertexList[stack[i]]);
}
}
}

//topSortHelper() function
function topSortHelper(v,visited,stack){
visited[v] = true;
for each(var w in this.adj[v]){
If(!visited[w]){
This.topSortHelper(visited[w],visited,stack);
}
}
​ stack.push(v);
}