 Technology peripherals
Technology peripherals AI
AI The performance of small models is saturated and the performance is poor. Is the root cause due to Softmax?
The performance of small models is saturated and the performance is poor. Is the root cause due to Softmax?The performance of small models is saturated and the performance is poor. Is the root cause due to Softmax?
The emergence of small language models is to make up for the disadvantages of expensive training and inference of large language models, but it also has the fact that its performance declines after training to a certain stage (saturation phenomenon). So what is the reason for this phenomenon? Can it be overcome and exploited to improve the performance of small language models?
The latest progress in the field of language modeling lies in pre-training highly parameterized neural networks on extremely large-scale web text corpora. In practice, using such a model for training and inference can be costly, prompting the use of smaller alternative models. However, it has been observed that smaller models may suffer from saturation and a phenomenon characterized by a decrease in capability and plateauing at some advanced stage of training.
A recent paper found that this saturation sum phenomenon can be explained by a mismatch between the latent dimensionality of the smaller model and the high rank of the target context probability distribution. This mismatch affects the performance of the linear prediction heads used in these models by employing what is known as the softmax bottleneck.

Paper link: https://arxiv.org/pdf/2404.07647.pdf
This article measures the impact of the softmax bottleneck under different settings. And it was found that models based on less than 1000 hidden dimensions tend to adopt degraded latent representations in the later stages of pre-training, resulting in reduced evaluation performance.
Introduction
The representation degradation problem is a common phenomenon that affects various modes such as self-supervised learning methods of text data. Observations of intermediate representations of language models reveal their low-angle variability (or anisotropy), or unusual dimensions that arise during training. However, these observations are mostly made on relatively small-scale models with dimensions comparable to family models such as BERT or GPT-2.
These models usually consist of a neural network f_θ that accepts a token sequence:

and generates a relatively low-dimensional R^d Context representation, where d is the hidden dimension of the model. They then rely on a language modeling head that produces the logarithm of the context token probabilities. A common choice for a language modeling head is a linear layer with parameters W ∈ R^(V×d), where V is the number of possible tokens. The resulting probability distribution for the next token is therefore  where σ is the softmax function.
where σ is the softmax function.
In the field of language modeling, the current trend is to extend the generative pre-training method introduced by GPT-2, which means training neural models composed of billions of parameters on huge corpus of web text. However, training and applying these highly parameterized models raises energy and hardware-related issues, which requires finding ways to achieve similar performance levels with smaller models.
However, evaluation of the Pythia model suite shows that training small models on very large corpora can lead to saturation, manifested by performance degradation late in pre-training. This paper explores this saturation phenomenon through the lens of representation degradation and finds that there is a strong correlation between the two phenomena, while further demonstrating that representation degradation occurs in language modeling heads of small models and has been demonstrated both theoretically and empirically. above shows how linear language modeling headers can become a performance bottleneck for architectures based on small hidden dimensions.
Language model saturation phenomenon
This article first verifies that it is indeed possible to observe and quantify performance saturation of Pythia checkpoints because they are the only release in the middle of a range of model sizes. checking point. This paper measures the cross-entropy of Pythia checkpoints on 50,000 tokens randomly sampled from their pre-training dataset (i.e., The Pile).
It can be clearly seen in Figure 1a that even the 410 million parameter model encounters saturation, manifested by increased in-domain loss at advanced training stages.

In Figure 1b, this paper fits the data points of the model starting from 410 million parameters according to the method of Hoffmann et al. (2022), and only optimizes Model-dependent constants (A and α), while reusing all other values (B = 410.7, β = 0.28, E = 1.69). Here we review the relationship between parameter count N and token count T given by Hoffmann et al. (2022):

This paper finds that the optimal parameters are A = 119.09 and α = 0.246. The authors show fitted curves of token counts corresponding to optimal and final checkpoints. It can be observed that the performance of the final checkpoint is on average about 8% lower than the extrapolated value. The loss-minimizing (optimal) checkpoint is expected to be lower than the extrapolation method due to incomplete learning rate cooling, but its performance is only about 4% lower than the extrapolation method.
A similar performance saturation phenomenon was also observed in the data set used for the evaluation of the language model evaluation tool (LM Evaluation Harness), as shown in Table 1.

Performance saturation is Rank Saturation
Scale Anisotropy
Anisotropy is a common form of representation degradation observed in various small language models, and it consists of reduced angular variability in the representation distribution in a specific layer. Previous research (Ethayarajh, 2019; Godey et al., 2024) noted that almost all layers of small deformed language models are anisotropic. A common way to measure anisotropy in a set of vector representations H is the average cosine similarity: model. To solve this problem, this paper calculates the average cosine similarity between layers for a series of model intermediate representations; namely GPT-2, OPT, Pythia and Gemma. This article uses a subsample of The Pile because it is assumed that the domain of this dataset includes or matches the domain of the pre-trained datasets used in these suites.
In Figure 2, it can be observed that most layers of most Transformer models are anisotropic to some extent, regardless of their scale. However, there seems to be a dichotomy in the last layer, where the model is either almost isotropic or highly anisotropic. This paper notes that this dichotomy is consistent with one of the saturation phenomena of the Pythia suite, where only models with 160 million parameters or fewer are affected by the anisotropy of the last layer. 
This article studies the training dynamics of anisotropy in the Pythia suite and compares it to the saturation phenomenon in Figure 3.

Figure 3 clearly demonstrates the clear correlation between the emergence of performance saturation phenomena and the emergence of anisotropy in the last layer representation of the model. It also shows a sudden increase in anisotropy near the saturation point during training. What is observed here is that in a specific in-domain corpus, the model rapidly loses performance upon saturation and never seems to fully recover from this explosion.
 Singular Value Saturation
Singular Value Saturation
Figure 4 shows the singular value distribution along the final prediction layer weight W during training:
Figure 4 reveals a specific pattern of spectral saturation , which occurs roughly at the same time as performance saturation. The figure shows that the singular value distribution gradually flattens during the training process, almost reaching uniformity, and then suddenly evolves into a spiked distribution with the largest singular value relatively high relative to other distributions.
To quantify this behavior more accurately, this article uses the singular entropy metric, calculated as the Kullback-Leibler divergence between the normalized singular value distribution and the uniform distribution. 

The inherent dimension of natural language
Intuitive In other words, the singular value distribution saturation phenomenon observed above only applies to smaller models, which calls into question the dimensions involved in the optimization of the LM head. This section proposes to empirically measure the critical value of the rank of an LM head and estimate the dimensions of the contextual probability distribution that the output of this head should match.To empirically measure the impact of linear head rank, this paper proposes to train a rank-restricted head on pre-trained contextual representations derived from highly parameterized language models. To control the maximum rank r, consider a head of the form W = AB ∈ R^(V×d), where the coefficients of A ∈ R^(V×r) and B ∈ R^(r×d) start from N(0 ,1) extracted (d is the hidden dimension of the model). The rank of this W matrix is scanned over a range of values constrained by the parameter r ∈ [1, d].
By freezing the language model and training the rank-restricted head on approximately 150 million tokens, while adjusting the learning rate to adapt to the number of trainable parameters.
It can be observed in Figure 6 that regardless of the model size, when the rank of the language modeling head W falls below 1000, the perplexity starts to decrease significantly. This implies that for models with larger hidden dimensions, the head is not a major performance bottleneck, but for models with smaller hidden dimensions it may hurt performance independently of the quality of the output representation.

Another interesting factor is the inherent dimensionality of the estimation data itself. In order to avoid possible effects related to specific inductive bias, this paper trained a naive 5-gram language model on several data sets with different coverage (IMDb, Wikitext, and The Pile), using two different vocabulary sizes. Tokenizer (30k tokens for Llama-2, 50k tokens for Pythia). Given C observed 5-grams, this paper considers the matrix W ∈ R^(C×V), where each row is the probability distribution of possible tokens given 4 tokens, and calculates their singular value distributions, such as Terashima (2003).
Figure 7 reports W-error, the minimum approximation error for a matrix W of rank d predicted by the Eckart-Young-Mirsky theorem (see Lemma 5.2) and normalized to the Frobenius of W norm.


Theoretical bottleneck
At the same time, the estimated rank of W is of the same order of magnitude as the hidden dimension It cannot be ignored in comparison. Here we will analyze the connection between the dimensions and performance of an ideal linear language modeling head from a theoretical perspective.
This section aims to identify the formal link between the inherent dimensions of context distributions and performance bottlenecks that can be attributed to the lower dimensionality of language model output representations. To this end, a language modeling head optimized on an ideal context representation is conceived, and the relationship between its spectral properties and the performance gap that arises when training a low-rank head on the same representation is explored.
For more research details, please view the original paper.
The above is the detailed content of The performance of small models is saturated and the performance is poor. Is the root cause due to Softmax?. For more information, please follow other related articles on the PHP Chinese website!
 The Hidden Dangers Of AI Internal Deployment: Governance Gaps And Catastrophic RisksApr 28, 2025 am 11:12 AM
The Hidden Dangers Of AI Internal Deployment: Governance Gaps And Catastrophic RisksApr 28, 2025 am 11:12 AMThe unchecked internal deployment of advanced AI systems poses significant risks, according to a new report from Apollo Research. This lack of oversight, prevalent among major AI firms, allows for potential catastrophic outcomes, ranging from uncont
 Building The AI PolygraphApr 28, 2025 am 11:11 AM
Building The AI PolygraphApr 28, 2025 am 11:11 AMTraditional lie detectors are outdated. Relying on the pointer connected by the wristband, a lie detector that prints out the subject's vital signs and physical reactions is not accurate in identifying lies. This is why lie detection results are not usually adopted by the court, although it has led to many innocent people being jailed. In contrast, artificial intelligence is a powerful data engine, and its working principle is to observe all aspects. This means that scientists can apply artificial intelligence to applications seeking truth through a variety of ways. One approach is to analyze the vital sign responses of the person being interrogated like a lie detector, but with a more detailed and precise comparative analysis. Another approach is to use linguistic markup to analyze what people actually say and use logic and reasoning. As the saying goes, one lie breeds another lie, and eventually
 Is AI Cleared For Takeoff In The Aerospace Industry?Apr 28, 2025 am 11:10 AM
Is AI Cleared For Takeoff In The Aerospace Industry?Apr 28, 2025 am 11:10 AMThe aerospace industry, a pioneer of innovation, is leveraging AI to tackle its most intricate challenges. Modern aviation's increasing complexity necessitates AI's automation and real-time intelligence capabilities for enhanced safety, reduced oper
 Watching Beijing's Spring Robot RaceApr 28, 2025 am 11:09 AM
Watching Beijing's Spring Robot RaceApr 28, 2025 am 11:09 AMThe rapid development of robotics has brought us a fascinating case study. The N2 robot from Noetix weighs over 40 pounds and is 3 feet tall and is said to be able to backflip. Unitree's G1 robot weighs about twice the size of the N2 and is about 4 feet tall. There are also many smaller humanoid robots participating in the competition, and there is even a robot that is driven forward by a fan. Data interpretation The half marathon attracted more than 12,000 spectators, but only 21 humanoid robots participated. Although the government pointed out that the participating robots conducted "intensive training" before the competition, not all robots completed the entire competition. Champion - Tiangong Ult developed by Beijing Humanoid Robot Innovation Center
 The Mirror Trap: AI Ethics And The Collapse Of Human ImaginationApr 28, 2025 am 11:08 AM
The Mirror Trap: AI Ethics And The Collapse Of Human ImaginationApr 28, 2025 am 11:08 AMArtificial intelligence, in its current form, isn't truly intelligent; it's adept at mimicking and refining existing data. We're not creating artificial intelligence, but rather artificial inference—machines that process information, while humans su
 New Google Leak Reveals Handy Google Photos Feature UpdateApr 28, 2025 am 11:07 AM
New Google Leak Reveals Handy Google Photos Feature UpdateApr 28, 2025 am 11:07 AMA report found that an updated interface was hidden in the code for Google Photos Android version 7.26, and each time you view a photo, a row of newly detected face thumbnails are displayed at the bottom of the screen. The new facial thumbnails are missing name tags, so I suspect you need to click on them individually to see more information about each detected person. For now, this feature provides no information other than those people that Google Photos has found in your images. This feature is not available yet, so we don't know how Google will use it accurately. Google can use thumbnails to speed up finding more photos of selected people, or may be used for other purposes, such as selecting the individual to edit. Let's wait and see. As for now
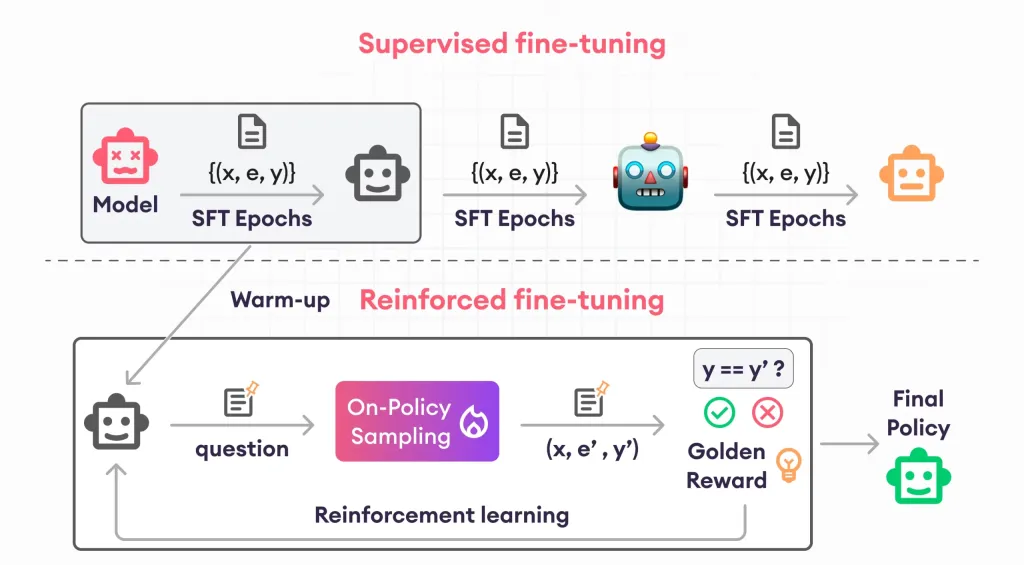 Guide to Reinforcement Finetuning - Analytics VidhyaApr 28, 2025 am 09:30 AM
Guide to Reinforcement Finetuning - Analytics VidhyaApr 28, 2025 am 09:30 AMReinforcement finetuning has shaken up AI development by teaching models to adjust based on human feedback. It blends supervised learning foundations with reward-based updates to make them safer, more accurate, and genuinely help
 Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AM
Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AMScientists have extensively studied human and simpler neural networks (like those in C. elegans) to understand their functionality. However, a crucial question arises: how do we adapt our own neural networks to work effectively alongside novel AI s


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

SublimeText3 Chinese version
Chinese version, very easy to use

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.





