CUDA's universal matrix multiplication: from entry to proficiency!

General Matrix Multiplication (GEMM) is a vital part of many applications and algorithms, and is also one of the important indicators for evaluating computer hardware performance. In-depth research and optimization of the implementation of GEMM can help us better understand high-performance computing and the relationship between software and hardware systems. In computer science, effective optimization of GEMM can increase computing speed and save resources, which is crucial to improving the overall performance of a computer system. An in-depth understanding of the working principle and optimization method of GEMM will help us better utilize the potential of modern computing hardware and provide more efficient solutions for various complex computing tasks. By optimizing and improving the performance of GEMM, we can add

1. Basic characteristics of GEMM

##1.1 GEMM calculation process and complexity

GEMM is defined as: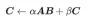

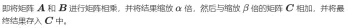
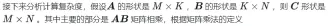
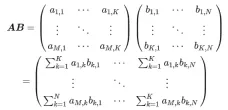
## Calculation diagram of matrix multiplication

1.2 Simple implementation and process analysis

The following is the code implemented on the CPU according to the original definition, which will later be used as a comparison of accuracy

#define OFFSET(row, col, ld) ((row) * (ld) + (col))void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K) {for (int m = 0; m <div>The following uses CUDA to implement the simplest Kernal matrix multiplication, in total Use M * N threads to complete the entire matrix multiplication. Each thread is responsible for the calculation of an element in matrix C and needs to complete K times of multiplication and accumulation. Matrices A, B, and C are all stored in global memory (determined by the modifier </div> <p><span>__global__</span><code style="background-color: rgb(231, 243, 237); padding: 1px 3px; border-radius: 4px; overflow-wrap: break-word; text-indent: 0px; display: inline-block;"> </code>). For the complete code, see sgemm_naive.cu. <span></span></p><pre class="brush:php;toolbar:false">__global__ void naiveSgemm(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {int n = blockIdx.x * blockDim.x + threadIdx.x;int m = blockIdx.y * blockDim.y + threadIdx.y;if (m <div>The compilation is completed and the results of execution on Tesla V100-PCIE-32GB are as follows. According to the V100 white paper, the peak computing power of FP32 is 15.7 TFLOPS, so the computing power utilization of this method is Only 11.5%. </div><p></p><pre class="brush:php;toolbar:false">M N K =128128 1024, Time = 0.00010083 0.00010260 0.00010874 s, AVG Performance = 304.5951 GflopsM N K =192192 1024, Time = 0.00010173 0.00010198 0.00010253 s, AVG Performance = 689.4680 GflopsM N K =256256 1024, Time = 0.00010266 0.00010318 0.00010384 s, AVG Performance =1211.4281 GflopsM N K =384384 1024, Time = 0.00019475 0.00019535 0.00019594 s, AVG Performance =1439.7206 GflopsM N K =512512 1024, Time = 0.00037693 0.00037794 0.00037850 s, AVG Performance =1322.9753 GflopsM N K =768768 1024, Time = 0.00075238 0.00075558 0.00075776 s, AVG Performance =1488.9271 GflopsM N K = 1024 1024 1024, Time = 0.00121562 0.00121669 0.00121789 s, AVG Performance =1643.8068 GflopsM N K = 1536 1536 1024, Time = 0.00273072 0.00275611 0.00280208 s, AVG Performance =1632.7386 GflopsM N K = 2048 2048 1024, Time = 0.00487622 0.00488028 0.00488614 s, AVG Performance =1639.2518 GflopsM N K = 3072 3072 1024, Time = 0.01001603 0.01071136 0.01099990 s, AVG Performance =1680.4589 GflopsM N K = 4096 4096 1024, Time = 0.01771046 0.01792170 0.01803462 s, AVG Performance =1785.5450 GflopsM N K = 6144 6144 1024, Time = 0.03988969 0.03993405 0.04000595 s, AVG Performance =1802.9724 GflopsM N K = 8192 8192 1024, Time = 0.07119219 0.07139694 0.07160816 s, AVG Performance =1792.7940 GflopsM N K =1228812288 1024, Time = 0.15978026 0.15993242 0.16043369 s, AVG Performance =1800.7606 GflopsM N K =1638416384 1024, Time = 0.28559187 0.28567238 0.28573316 s, AVG Performance =1792.2629 Gflops

The following takes M=512, K=512, N=512 as an example to analyze the workflow of the above calculation process in detail:

1. In Global Memory, they are matrices A, B, and C respectively. Allocate storage space.
2. Since the calculation of each element in matrix C is independent of each other, in the parallelism mapping, each thread corresponds to the calculation of 1 element in matrix C.
3. Execution Both gridSize and blockSize in the execution configuration have two dimensions: x (column direction) and y (row direction), where

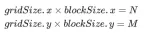
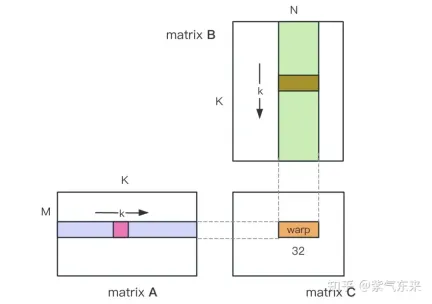
Profiling of the naive version recorded by nsys

2. GEMM optimization exploration

The previous article only implemented GEMM functionally, and the performance was far from expected. This section will mainly study the optimization of GEMM performance.

2.1 Matrix partitioning using Shared Memory

The above calculation requires two Global Memory loads to complete a multiplication and accumulation operation. The calculation memory access ratio is extremely low, no Efficient data reuse. Therefore, Shared Memory can be used to reduce repeated memory reads.

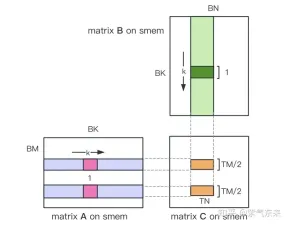
First divide the matrix C into equal blocks of BMxBN size. Each block is calculated by a Block, in which each Thread is responsible for calculating the TMxTN elements in the matrix C. Afterwards, all the data required for calculation is read from smem, which eliminates part of the repeated memory reading of A and B matrices. Considering that Shared Memory has limited capacity, BK-sized blocks can be read in K dimensions each time. Such a loop requires a total of K / BK times to complete the entire matrix multiplication operation, and the result of the Block can be obtained. The process is shown in the figure below:

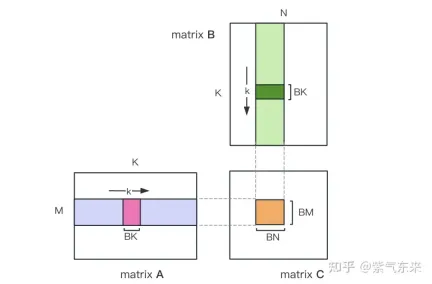
After optimization using Shared Memory, for each block, we can get:

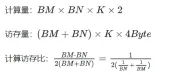
It can be seen from the above formula that the larger the BM and BN are, the higher the calculation memory access ratio will be and the better the performance will be. However, due to the limitation of Shared Memory capacity (V100 1 SM is only 96KB), a Block needs to occupy BK * (BM BN) * 4 Bytes.

The values ​​​​of TM and TN are also limited by two aspects. On the one hand, there are restrictions on the number of threads. There are BM / TM * BN / TN threads in a Block. This number cannot exceed 1024, and cannot be too high to prevent affecting SM. Parallelism between inner blocks; on the other hand, there is a limit on the number of registers. A thread requires at least TM * TN registers to store the partial sum of matrix C, plus some other registers. The number of all registers cannot exceed 256, and It cannot be too high to avoid affecting the number of parallel threads in SM at the same time.

Finally select BM = BN = 128, BK = 8, TM = TN = 8, then the calculated memory access ratio is 32. According to the theoretical computing power of V100 15.7TFLOPS, we can get 15.7TFLOPS/32 = 490GB/s. According to the measured HBM bandwidth is 763GB/s, it can be seen that the bandwidth will no longer limit the computing performance at this time.

Based on the above analysis, the kernel function implementation process is as follows. For the complete code, see sgemm_v1.cu. The main steps include:

##A B matrix block thread index relationship

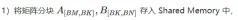
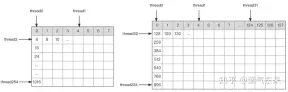
After determining the execution process of a single block, it is necessary to determine the corresponding relationship between the different blocks processed by multi-block in Global Memory. A is still used as an example for explanation. Since the block moves along the direction of the row, you first need to determine the row number. According to the two-dimensional global linear index relationship of the Grid, by * BM represents the starting row of the block At the same time, we know that load_a_smem_m is the line number inside the block, so the global line number is load_a_gmem_m = by * BM load_a_smem_m . Since the blocks move along the row direction, the columns change and need to be calculated inside the loop. The starting column number is also calculated first bk * BK Accelerate the internal columns of the blocks No.load_a_smem_k Get load_a_gmem_k = bk * BK load_a_smem_k , from which we can determine the block location Position OFFSET(load_a_gmem_m, load_a_gmem_k, K) in the original data. In the same way, the matrix partitioning situation can be analyzed and will not be repeated.

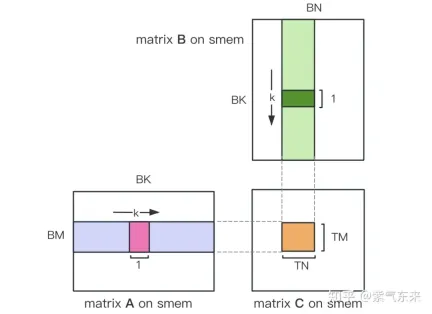
After the calculation is completed, it needs to be stored in Global Memory, which requires calculating its corresponding relationship in Global Memory. Due to the existence of smaller chunks, both rows and columns are composed of 3 parts: the global row number store_c_gmem_m is equal to the starting row number of the large chunk by * BM The starting line number of the small block ty * TM The relative line number inside the small block i . The same goes for columns.

__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {const int BM = 128;const int BN = 128;const int BK = 8;const int TM = 8;const int TN = 8;const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = ty * blockDim.x + tx;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;// tid/2, row of s_aint load_a_smem_k = (tid & 1) > 5; // tid/32, row of s_bint load_b_smem_n = (tid & 31) 

The calculation results are as follows, the performance reaches 51.7% of the theoretical peak performance:

M N K =128128 1024, Time = 0.00031578 0.00031727 0.00032288 s, AVG Performance =98.4974 GflopsM N K =192192 1024, Time = 0.00031638 0.00031720 0.00031754 s, AVG Performance = 221.6661 GflopsM N K =256256 1024, Time = 0.00031488 0.00031532 0.00031606 s, AVG Performance = 396.4287 GflopsM N K =384384 1024, Time = 0.00031686 0.00031814 0.00032080 s, AVG Performance = 884.0425 GflopsM N K =512512 1024, Time = 0.00031814 0.00032007 0.00032493 s, AVG Performance =1562.1563 GflopsM N K =768768 1024, Time = 0.00032397 0.00034419 0.00034848 s, AVG Performance =3268.5245 GflopsM N K = 1024 1024 1024, Time = 0.00034570 0.00034792 0.00035331 s, AVG Performance =5748.3952 GflopsM N K = 1536 1536 1024, Time = 0.00068797 0.00068983 0.00069094 s, AVG Performance =6523.3424 GflopsM N K = 2048 2048 1024, Time = 0.00136173 0.00136552 0.00136899 s, AVG Performance =5858.5604 GflopsM N K = 3072 3072 1024, Time = 0.00271910 0.00273115 0.00274006 s, AVG Performance =6590.6331 GflopsM N K = 4096 4096 1024, Time = 0.00443805 0.00445964 0.00446883 s, AVG Performance =7175.4698 GflopsM N K = 6144 6144 1024, Time = 0.00917891 0.00950608 0.00996963 s, AVG Performance =7574.0999 GflopsM N K = 8192 8192 1024, Time = 0.01628838 0.01645271 0.01660790 s, AVG Performance =7779.8733 GflopsM N K =1228812288 1024, Time = 0.03592557 0.03597434 0.03614323 s, AVG Performance =8005.7066 GflopsM N K =1638416384 1024, Time = 0.06304122 0.06306373 0.06309302 s, AVG Performance =8118.7715 Gflops

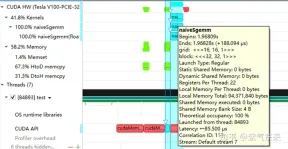
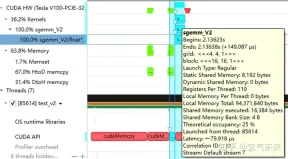
The following is still taking M=512, K=512, N=512 as an example to analyze the results. First, through profiling, we can see that the Shared Memory occupies 8192 bytes, which is completely consistent with the theory (128 128) X8X4.

The profiling of the V1 version recorded by nsys

profiling shows that the Occupancy is 12.5%, which can be confirmed by cuda-calculator. In this example, threads per block = 256, Registers per thread = 136, it can be calculated that the active warps in each SM are 8, and for V100, the total number of warps in each SM is 64, so the Occupancy is 8/64 = 12.5%.

2.2 Solve the Bank Conflict problem

The previous section greatly improved the memory access efficiency by using Shared Memory, thereby improving performance. This section will further optimize the use of Shared Memory.

Shared Memory is divided into 32 Banks, and the width of each Bank is 4 Bytes. If multiple data of the same Bank need to be accessed, Bank Conflict will occur. For example, if there are 32 threads in a Warp, if the accessed addresses are 0, 4, 8, ..., 124, Bank Conflict will not occur, and only one beat of Shared Memory will be occupied; if the accessed addresses are 0, 8 , 16,..., 248, so that the data corresponding to address 0 and address 128 are located in the same Bank, the data corresponding to address 4 and address 132 are located in the same Bank, and so on, then it will take up two beats of Shared Memory time can be read out.

With Bank Conflict VS without Bank Conflict

Let’s look at the three-layer loop in the calculation part of the V1 version. Each time, the length of matrix A is taken from Shared memory. is the vector of TM and the vector of length TN of matrix B. These two vectors do an outer product and are accumulated into the partial sum. One outer product is a total of TM * TN times of multiplication and accumulation. A total of BK times of counting and outer product need to be looped.

Next, analyze the Bank Conflict that exists in the process of Shared Memory load:

i) To obtain matrix A, you need to obtain a column vector, and matrix A is stored row by row in Shared Memory. ;

ii) In the case of TM = TN = 8, no matter matrix A or matrix B, when fetching numbers from Shared Memory, 8 consecutive numbers need to be fetched, that is, using the LDS.128 instruction to fetch in one instruction Four numbers also require two instructions. Since the addresses of two load instructions in one thread are consecutive, the memory access addresses of the same load instruction in different threads of the same Warp are separated, and there is a Bank Conflict. .

In order to solve the above two points of Bank Conflict of Shared Memory, two optimization points are adopted:

i) When allocating Shared Memory to matrix A, the shape is allocated as [BK][BM], That is, let matrix A be stored column-by-column in Shared Memory

ii) Divide the TM * TN matrix C that each thread is responsible for calculating into two TM/2 * TN matrices C as shown in the figure below. Since TM/2=4, one instruction can complete it A piece of load operation, two loads can be performed at the same time.

#The core part of the kernel function is implemented as follows. For the complete code, see sgemm_v2.cu.

__shared__ float s_a[BK][BM];__shared__ float s_b[BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

The results are as follows. Compared with the unresolved Bank Conflict version (V1), the performance has improved by 14.4%, reaching 74.3% of the theoretical peak.

M N K =128128 1024, Time = 0.00029699 0.00029918 0.00030989 s, AVG Performance = 104.4530 GflopsM N K =192192 1024, Time = 0.00029776 0.00029828 0.00029882 s, AVG Performance = 235.7252 GflopsM N K =256256 1024, Time = 0.00029485 0.00029530 0.00029619 s, AVG Performance = 423.2949 GflopsM N K =384384 1024, Time = 0.00029734 0.00029848 0.00030090 s, AVG Performance = 942.2843 GflopsM N K =512512 1024, Time = 0.00029853 0.00029945 0.00030070 s, AVG Performance =1669.7479 GflopsM N K =768768 1024, Time = 0.00030458 0.00032467 0.00032790 s, AVG Performance =3465.1038 GflopsM N K = 1024 1024 1024, Time = 0.00032406 0.00032494 0.00032621 s, AVG Performance =6155.0281 GflopsM N K = 1536 1536 1024, Time = 0.00047990 0.00048224 0.00048461 s, AVG Performance =9331.3912 GflopsM N K = 2048 2048 1024, Time = 0.00094426 0.00094636 0.00094992 s, AVG Performance =8453.4569 GflopsM N K = 3072 3072 1024, Time = 0.00187866 0.00188096 0.00188538 s, AVG Performance =9569.5816 GflopsM N K = 4096 4096 1024, Time = 0.00312589 0.00319050 0.00328147 s, AVG Performance = 10029.7885 GflopsM N K = 6144 6144 1024, Time = 0.00641280 0.00658940 0.00703498 s, AVG Performance = 10926.6372 GflopsM N K = 8192 8192 1024, Time = 0.01101130 0.01116194 0.01122950 s, AVG Performance = 11467.5446 GflopsM N K =1228812288 1024, Time = 0.02464854 0.02466705 0.02469344 s, AVG Performance = 11675.4946 GflopsM N K =1638416384 1024, Time = 0.04385955 0.04387468 0.04388355 s, AVG Performance = 11669.5995 Gflops

Analyzing the profiling, you can see that Static Shared Memory still uses 8192 Bytes. The strange thing is that Shared Memory executed doubled to 16384 Bytes (if you know Can you tell me the reason).

2.3 Pipeline parallelization: Double Buffering

Double Buffering, that is, double buffering, that is, by increasing the buffer, so that Memory access-calculation The serial mode of is pipelined to reduce waiting time and improve calculation efficiency. The principle is shown in the figure below:

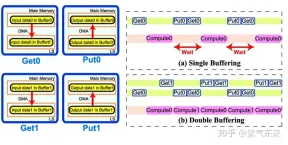
Single Buffering VS Double Buffering

Specifically speaking to the GEMM task, twice the Shared Memory is needed. Previously, only BK * (BM BN) * 4 Bytes of Shared Memory was needed. , after using Double Buffering, a Shared Memory of 2BK * (BM BN) * 4 Bytes is required, and then the pipeline can flow.

The core part of the code is as follows. For the complete code, see sgemm_v3.cu. There are the following points to note:

1) The main loop starts from bk = 1 . The first data load is before the main loop, and the last calculation is after the main loop. After the loop, this is determined by the characteristics of the pipeline;

2) Since the Shared Memory used for calculation and next memory access is different, only one __syncthreads() is needed for each loop in the main loop

3) Since the GPU cannot support out-of-order execution like the CPU, the main loop needs to first load the data in the Gloabal Memory required for the next loop calculation into the register, then perform this calculation, and then load it into the register. The data in is written to the Shared Memory, so that when the LDG instruction loads the Global Memory, it will not affect the subsequent launch execution of FFMA and other operation instructions, thus achieving the purpose of Double Buffering.

__shared__ float s_a[2][BK][BM];__shared__ float s_b[2][BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

Performance is shown below, reaching 80.6% of the theoretical peak.

M N K =128128 1024, Time = 0.00024000 0.00024240 0.00025792 s, AVG Performance = 128.9191 GflopsM N K =192192 1024, Time = 0.00024000 0.00024048 0.00024125 s, AVG Performance = 292.3840 GflopsM N K =256256 1024, Time = 0.00024029 0.00024114 0.00024272 s, AVG Performance = 518.3728 GflopsM N K =384384 1024, Time = 0.00024070 0.00024145 0.00024198 s, AVG Performance =1164.8394 GflopsM N K =512512 1024, Time = 0.00024173 0.00024237 0.00024477 s, AVG Performance =2062.9786 GflopsM N K =768768 1024, Time = 0.00024291 0.00024540 0.00026010 s, AVG Performance =4584.3820 GflopsM N K = 1024 1024 1024, Time = 0.00024534 0.00024631 0.00024941 s, AVG Performance =8119.7302 GflopsM N K = 1536 1536 1024, Time = 0.00045712 0.00045780 0.00045872 s, AVG Performance =9829.5167 GflopsM N K = 2048 2048 1024, Time = 0.00089632 0.00089970 0.00090656 s, AVG Performance =8891.8924 GflopsM N K = 3072 3072 1024, Time = 0.00177891 0.00178289 0.00178592 s, AVG Performance = 10095.9883 GflopsM N K = 4096 4096 1024, Time = 0.00309763 0.00310057 0.00310451 s, AVG Performance = 10320.6843 GflopsM N K = 6144 6144 1024, Time = 0.00604826 0.00619887 0.00663078 s, AVG Performance = 11615.0253 GflopsM N K = 8192 8192 1024, Time = 0.01031738 0.01045051 0.01048861 s, AVG Performance = 12248.2036 GflopsM N K =1228812288 1024, Time = 0.02283978 0.02285837 0.02298272 s, AVG Performance = 12599.3212 GflopsM N K =1638416384 1024, Time = 0.04043287 0.04044823 0.04046151 s, AVG Performance = 12658.1556 Gflops

From profiling, you can see double the Shared Memory occupation

3. Exploration of cuBLAS implementation

This section We will get to know CUDA's standard library - cuBLAS, the NVIDIA version of the Basic Linear Algebra Subprograms (BLAS) specification implementation code. It supports standard matrix operations at Level 1 (vector and vector operations), Level 2 (vector and matrix operations), and Level 3 (matrix and matrix operations).

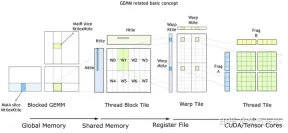
The basic process of cuBLAS/CUTLASS GEMM

As shown in the figure above, the calculation process is decomposed into thread block tiles(thread block tile ), thread bundle piece(warp tile) and thread piece(thread tile) hierarchical structure and apply AMP's strategy to this hierarchical structure to efficiently complete GPU-based teardown. GEMM divided into tiles. This hierarchy closely reflects the NVIDIA CUDA programming model. You can see data movement from global memory to shared memory (matrix to thread block tile); data movement from shared memory to registers (thread block tile to warp tile); calculations from registers to CUDA core (warp tile to thread tile) ).

cuBLAS implements the single-precision matrix multiplication function cublasSgemm. Its main parameters are as follows:

cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 cublasOperation_t transa, // A 矩阵是否需要转置 cublasOperation_t transb, // B 矩阵是否需要转置 int m, // A 的行数 int n, // B 的列数 int k, // A 的列数 const float *alpha, // 系数 α, host or device pointer const float *A, // 矩阵 A 的指针，device pointer int lda, // 矩阵 A 的主维，if A 转置， lda = max(1, k), else max(1, m) const float *B, // 矩阵 B 的指针, device pointer int ldb, // 矩阵 B 的主维，if B 转置， ldb = max(1, n), else max(1, k) const float *beta, // 系数 β, host or device pointer float *C, // 矩阵 C 的指针，device pointer int ldc // 矩阵 C 的主维，ldc >= max(1, m) );

The calling method is as follows:

cublasHandle_t cublas_handle;cublasCreate(&cublas_handle);float cublas_alpha = 1.0;float cublas_beta = 0;cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);

Performance is shown below, reaching 82.4% of the theoretical peak.

M N K =128128 1024, Time = 0.00002704 0.00003634 0.00010822 s, AVG Performance = 860.0286 GflopsM N K =192192 1024, Time = 0.00003155 0.00003773 0.00007267 s, AVG Performance =1863.6689 GflopsM N K =256256 1024, Time = 0.00003917 0.00004524 0.00007747 s, AVG Performance =2762.9438 GflopsM N K =384384 1024, Time = 0.00005318 0.00005978 0.00009120 s, AVG Performance =4705.0655 GflopsM N K =512512 1024, Time = 0.00008326 0.00010280 0.00013840 s, AVG Performance =4863.9646 GflopsM N K =768768 1024, Time = 0.00014278 0.00014867 0.00018816 s, AVG Performance =7567.1560 GflopsM N K = 1024 1024 1024, Time = 0.00023485 0.00024460 0.00028150 s, AVG Performance =8176.5614 GflopsM N K = 1536 1536 1024, Time = 0.00046474 0.00047607 0.00051181 s, AVG Performance =9452.3201 GflopsM N K = 2048 2048 1024, Time = 0.00077930 0.00087862 0.00092307 s, AVG Performance =9105.2126 GflopsM N K = 3072 3072 1024, Time = 0.00167904 0.00168434 0.00171114 s, AVG Performance = 10686.6837 GflopsM N K = 4096 4096 1024, Time = 0.00289619 0.00291068 0.00295904 s, AVG Performance = 10994.0128 GflopsM N K = 6144 6144 1024, Time = 0.00591766 0.00594586 0.00596915 s, AVG Performance = 12109.2611 GflopsM N K = 8192 8192 1024, Time = 0.01002384 0.01017465 0.01028435 s, AVG Performance = 12580.2896 GflopsM N K =1228812288 1024, Time = 0.02231159 0.02233805 0.02245619 s, AVG Performance = 12892.7969 GflopsM N K =1638416384 1024, Time = 0.03954650 0.03959291 0.03967242 s, AVG Performance = 12931.6086 Gflops

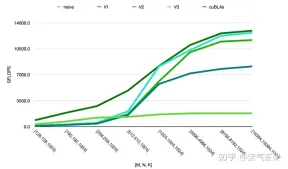
The performance of the above methods can be compared. It can be seen that the performance of manual implementation is close to the official performance, as follows:

The above is the detailed content of CUDA's universal matrix multiplication: from entry to proficiency!. For more information, please follow other related articles on the PHP Chinese website!